Экзаменационная работа по геометрии на тему

“Симедиана”

Ученика 9 кл. Ц.О. №218

Зерцалова Андрея

Руководитель: Блинков

Юрий Александрович

Москва 2012 г.

Оглавление:

Часть I Определение симедианы
1.1 Определения и их эквивалентность . . . . . . . . . . . . . . . . . . . . . . .	2
1.2 Симедиана и антипараллельность . . . . . . . . . . . . . . . . . . . . . . . .	4
1.3 Симедиана и ортоизогональ . . . . . . . . . . . . . . . . . . . . . . . . . . . .	6
1.4 Симедиана и подобие. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
1.5 Симедиана и изогональное сопряжение . . . . . . . . . . . . . . . . . . . .	9
Часть II Основная задача
2.1 Симедиана и инверсия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	10
2.2 Основная задача и её применение . . . . . . . . . . . . . . . . . . . . . . . .	15
Часть III. Гармонический четырехугольник
3.1 Определение гармонического четырехугольника . . . . . . . . . . . . .	19
3.2 Связь и симедианой и свойство . . . . . . . . . . . . . . . . . . . . . . . . . .	19
3.3 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20

Часть I. Определение симедианы

1.1 Определения и их эквивалентность

А) Рассмотрим треугольник АВС, его медиану АМ и биссектрису AL. Пусть прямая AN симметрична прямой АМ относительно прямой AL (N лежит на отрезке BC). Тогда отрезок AN называется симедианой треугольника АВС.

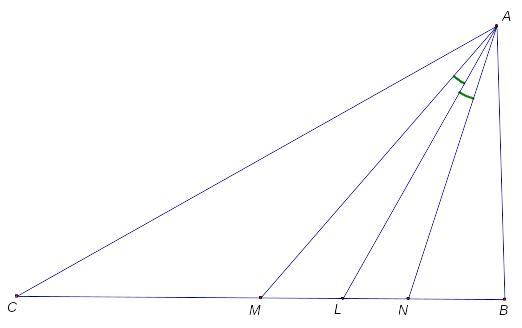
Б) Точка N лежит на стороне BC треугольника ABC. AN является симедианой треугольника ABC тогда и только тогда, когда BN/CN = AB²/AC².

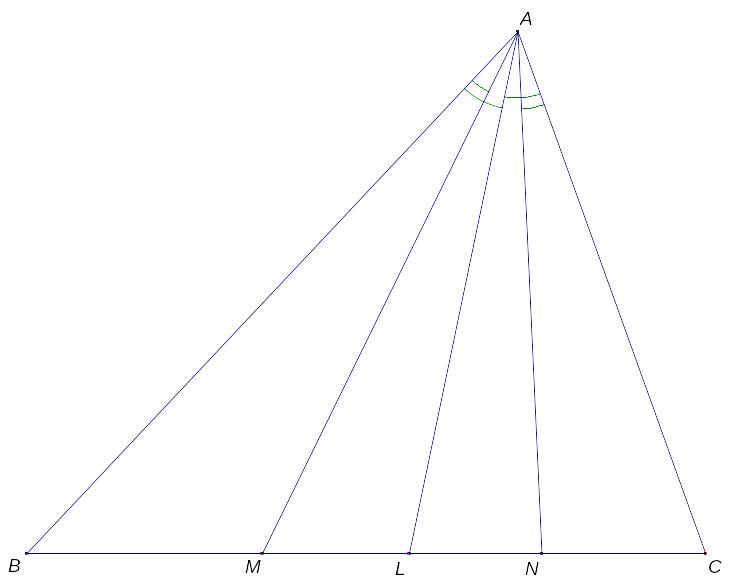
Докажем вспомогательное утверждение: Прямые AM и AN симметричны относительно биссектрисы угла A треугольника ABC (точки M и N лежат на прямой BC ). Докажите, что BM ^. BN/(CM ^. CN) = AB²/AC².

Доказательство:

Пусть

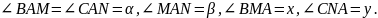
Запишем теорему синусов: 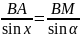(для △BAM); 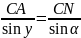(для △CAN); 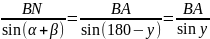(для △BAN); (для △CAM)

Таким образом,

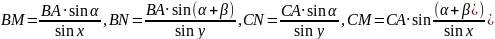
Подставим полученные выражения в формулу:

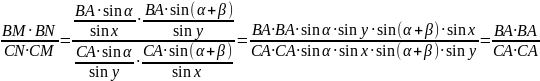, что и требовалось.

Докажем эквивалентность двух определений.

1) Если AN – симедиана, то BM = MC, следовательно, 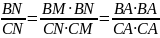, что и требовалось.

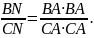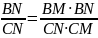2) Пусть С другой стороны, по лемме, , то есть BM = MC. Следовательно, прямая, симметричная AN относительно AL является медианой. Таким образом, эти определения эквивалентны.

Ч.Т.Д.

1.2 Симедиана и антипараллельность

1.2.1 В треугольнике АВС проведен отрезок В₁С₁, антипараллельный стороне ВС, с концами на сторонах АВ и АС соответственно. Докажите, что отрезок AS (S[BC]) является симедианой треугольника т. и т. т., когда он, пересекая отрезок В₁С₁, делит его пополам.

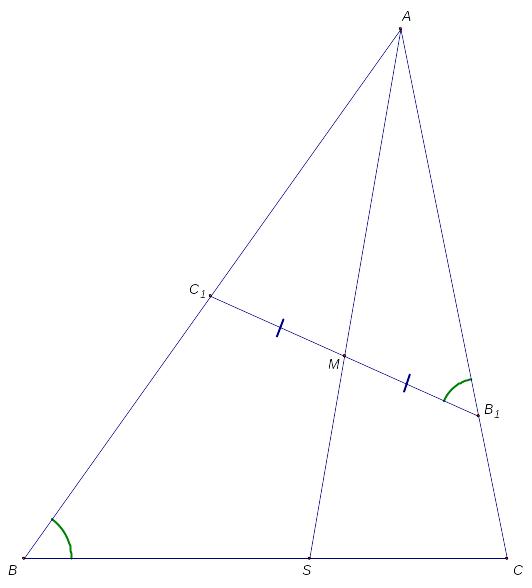
Доказательство:

Рассмотрим симметрию относительно биссектрисы угла А. Образы точек В₁ и С₁ принадлежат прямым АВ и АС соответственно, причем полученный отрезок параллелен прямой ВС. Следовательно, его середина лежит на медиане треугольника АВС тогда и только тогда, когда AS – симедиана (по первому определению).

Ч.Т.Д.

1.2.2 (Московская математическая олимпиада 2008) Высоты AA₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H . Точка B₀ – середина стороны AC . Докажите, что точка пересечения прямых, симметричных BB₀ и HB₀ относительно биссектрис углов ABC и AHC соответственно, лежит на прямой A₁C₁.

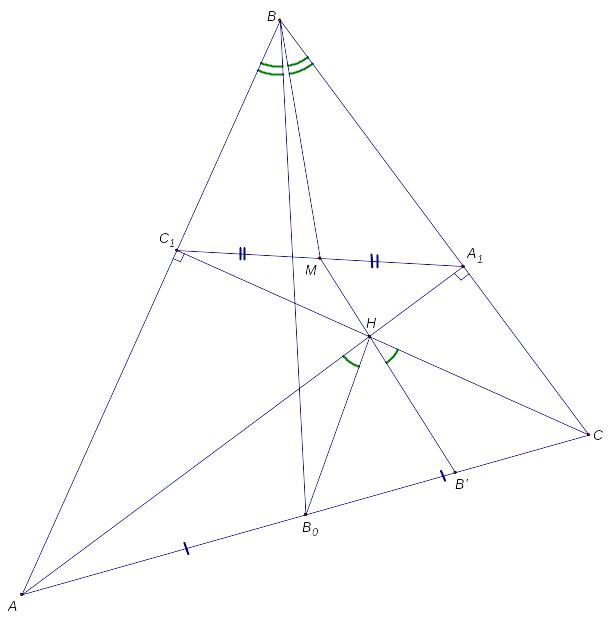
Доказательство:

Заметим, что A₁C₁ – прямая, антипараллельная BC. Из задачи №1.2.1 следует, что прямая, симметричная BB₀ относительно BL проходит через середину С₁A₁ (точку М). Аналогично, прямая, симметричная HB₀, относительно биссектрисы угла АНС, проходит через точку М.

Ч.Т.Д.