
- •Оглавление:
- •Введение
- •Часть I. Определение симедианы
- •1.1 Определения и их эквивалентность
- •1.2 Симедиана и антипараллельность
- •1.3 Симедиана и ортоизогональ
- •1.4 Симедиана и подобие
- •1.5 Симедиана и изогональное сопряжение
- •Часть II. Основная задача
- •2.1 Симедиана и инверсия
- •2.2 Основная задача и её применение
- •Часть III. Гармонический четырехугольник
- •3.1 Определение гармонического четырехугольника
- •3.2 Связь с симедианой (свойство)
- •3.3 Задачи
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •Заключение
- •Список литературы и web-ресурсов
1.5 Симедиана и изогональное сопряжение
1.5.1
(Московская
устная олимпиада по геометрии 2009)
К
двум окружностям w1
и
w2,
пересекающимся в точках
и
,
проведена их общая касательная
(
и
— точки касания соответственно, точка
ближе к прямой
,
чем
).
Прямая, проходящая через
,
вторично пересекает w1
и w2
в точках
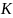 и
и
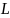 соответственно (
лежит между
и
).
Прямые
соответственно (
лежит между
и
).
Прямые
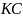 и
и
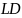 пересекаются в точке
пересекаются в точке
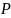 .
Докажите, что
.
Докажите, что
 —
симедиана треугольника
—
симедиана треугольника
 .
.
Доказательство:
1)
Докажем, что
 .
Из теоремы об угле между касательной и
хордой следует, что
.
Из теоремы об угле между касательной и
хордой следует, что
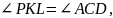 а
а
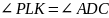 .
Таким образом, треугольники подобны по
двум углам.
.
Таким образом, треугольники подобны по
двум углам.
2) Продлим общую хорду до пересечения с общей касательной (точка ). Точка будет серединой отрезка .
3)
Так как треугольники подобны, то если
провести медиану
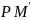 треугольника
треугольника
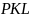 ,
то
,
то
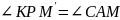 .
Заметим, что, если доказать равенство
углов
.
Заметим, что, если доказать равенство
углов
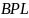 и
,
то угол
будет равен углу
и
,
то угол
будет равен углу
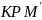 ,
то есть
– симедиана треугольника
(по первому
определению).
Известно, что
,
то есть
– симедиана треугольника
(по первому
определению).
Известно, что
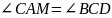 .
Таким образом, нужно доказать, что
четырехугольник
.
Таким образом, нужно доказать, что
четырехугольник
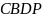 – вписанный. Рассмотрим треугольник
– вписанный. Рассмотрим треугольник
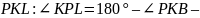
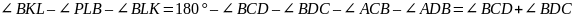 .
При этом,
.
При этом,
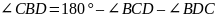 ,
следовательно,
,
следовательно,
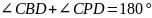 ,
что и требовалось.
,
что и требовалось.
Часть II. Основная задача
2.1 Симедиана и инверсия
2.1.1
В окружности с центром
проведена хорда
.
Через точку
– середину этой хорды проведен диаметр
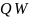 .
Лучи
.
Лучи
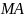 и
и
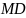 таковы, что
таковы, что
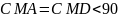 (
и
– точки пересечения этих лучей с
окружностью лежат в одной полуплоскости
относительно прямой
).
(
и
– точки пересечения этих лучей с
окружностью лежат в одной полуплоскости
относительно прямой
).
А)
Докажите,
что одна из симедиан треугольника
лежит на прямой
 .
.
W
Доказательство:
Докажем,
что
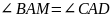 .
Продлим
до пересечения с окружностью (см.рис).
Тогда точки
.
Продлим
до пересечения с окружностью (см.рис).
Тогда точки
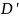 и
симметричны относительно диаметра
и
симметричны относительно диаметра
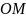 .
Следовательно,
.
Следовательно,
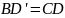 ,
то есть
,
то есть
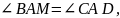 что и требовалось.
что и требовалось.
Б)
Докажите,
что четырехугольник
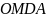 – вписанный.
– вписанный.

Доказательство:
Заметим,
что
 Таким
образом,
Таким
образом,
 – вписанный четырехугольник.
– вписанный четырехугольник.
В) Докажите, что все прямые , построенные таким образом, пересекают прямую в одной и той же точке , инверсной относительно данной окружности.
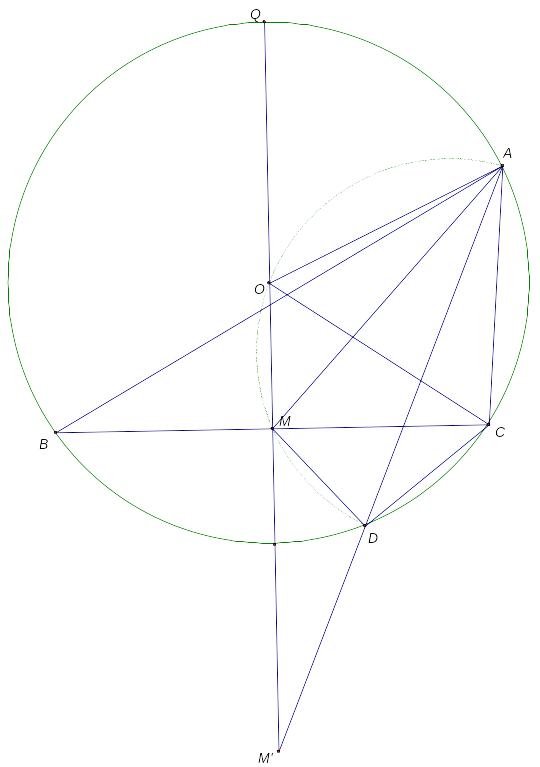
Доказательство:
Пусть – образ точки при инверсии относительно данной окружности (см. рис). Окружность, описанная около четырехугольника , переходит в прямую (поскольку точки и принадлежат окружности инверсии). Тогда точка принадлежит прямой .
С другой стороны, точка лежит на прямой и не зависит от положения прямой . Следовательно, все прямые проходят через фиксированную точку (образ точки при инверсии относительно данной окружности).
Комментарий: пункт В иногда называют теоремой о симметричной бабочке.
2.1.2
Точки
,
и
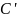 — середины сторон
,
— середины сторон
,
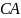 и
треугольника
соответственно, а
и
треугольника
соответственно, а
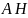 — его высота. Окружности, описанные
около треугольников
— его высота. Окружности, описанные
около треугольников
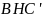 и
и
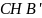 проходят через точку
,
отличную от
проходят через точку
,
отличную от
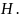
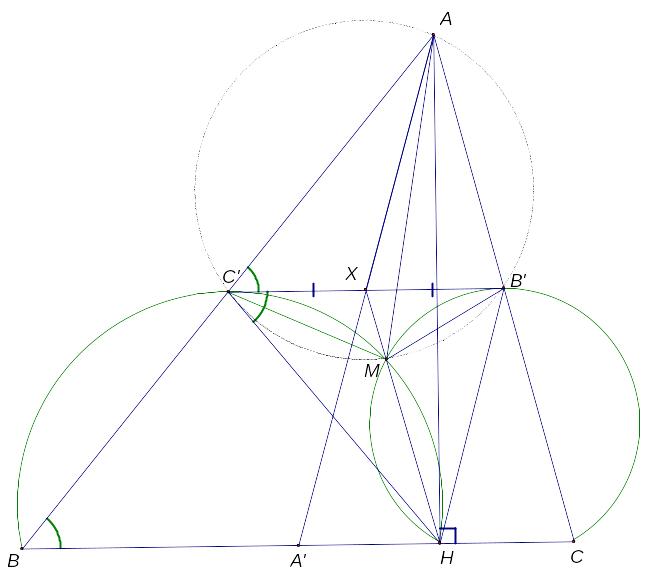
А)
(Международная
олимпиада по математике, 1970)
Докажите,
что четырехугольник
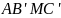 – вписанный,
а
прямая
– вписанный,
а
прямая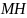 проходит
через середину
проходит
через середину
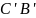 .
.
Б)
(Московская
математическая олимпиада
2007)
Докажите, что
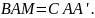
Доказательство:
1)
Докажем, что
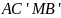 –
вписанный. Действительно, ∠
–
вписанный. Действительно, ∠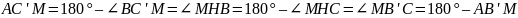 ,
что и требовалось.
,
что и требовалось.
Поскольку
мы пользовались только тем, что
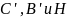 принадлежат
сторонам треугольника, то доказано
более общее утверждение:
если взять точки
принадлежат
сторонам треугольника, то доказано
более общее утверждение:
если взять точки
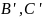 и
на сторонах треугольника
,
и
соответственно,
то окружности, описанные около
треугольников
и
на сторонах треугольника
,
и
соответственно,
то окружности, описанные около
треугольников
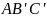 ,
,
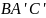 и
и
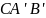 пересекаются
в
одной
точке.
пересекаются
в
одной
точке.
2)
Докажем, что
–
общая касательная для окружностей,
описанных около треугольников
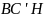 и
и
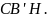
Заметим,
что треугольники
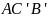 и
и
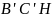 симметричны
относительно
.
Из этого следует, что
симметричны
относительно
.
Из этого следует, что
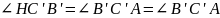 .
По теореме об угле между касательной и
хордой
–
касательная к окружности, описанной
около треугольника
.
Для окружности описанной около
.
По теореме об угле между касательной и
хордой
–
касательная к окружности, описанной
около треугольника
.
Для окружности описанной около
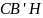 доказательство
аналогично.
доказательство
аналогично.
3) MH – общая хорда, следовательно прямая пересекает общую касательную в середине отрезка . Таким образом, пункт А) доказан.
4)
Теперь рассмотрим окружность, описанную
около четырехугольника
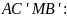
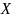 –
середина хорды
–
середина хорды
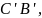 лучи
лучи
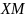 и
и
 симметричны
относительно
.
Из Задачи
№2.1.1(А) следует,
что
– симедиана в треугольнике
,
а следовательно, и в треугольнике
,
так как эти треугольники гомотетичны
с центром
.
симметричны
относительно
.
Из Задачи
№2.1.1(А) следует,
что
– симедиана в треугольнике
,
а следовательно, и в треугольнике
,
так как эти треугольники гомотетичны
с центром
.
2.1.3
Точки
и
инверсны
относительно окружности ,
причем
– внутри .
Через
проводятся хорды
 .
Докажите, что центры вписанной и одной
из вневписанных окружностей треугольника
.
Докажите, что центры вписанной и одной
из вневписанных окружностей треугольника
 –
фиксированы.
–
фиксированы.

Доказательство:
Пусть
 – точка пересечения
– точка пересечения
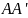 с окружностью, а
с окружностью, а
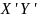 – хорда, проходящая через
,
перпендикулярная диаметру.
– хорда, проходящая через
,
перпендикулярная диаметру.
1)
Из задачи
№2.1.1
следует, что
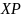 –
симедиана в треугольнике
–
симедиана в треугольнике
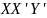 ,
а
,
а
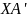 –
медиана, следовательно точки
и
–
медиана, следовательно точки
и
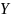 симметричны относительно прямой
симметричны относительно прямой
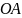 .
Таким образом,
.
Таким образом,
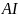 –биссектриса в треугольнике
.
–биссектриса в треугольнике
.
2) Заметим, что – точка пересечения двух биссектрис в треугольнике , следовательно – инцентр данного треугольника.
3)
Рассмотрим
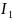 ,
диаметрально противоположную
.
,
диаметрально противоположную
.
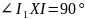 ,
следовательно
,
следовательно
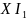 – биссектриса внешнего угла треугольника
– биссектриса внешнего угла треугольника
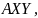 а
–
биссектриса внутреннего угла. Таким
образом,
–
точка пересечения биссектрис внешнего
и внутреннего углов треугольника, то
есть
–
центр вневписанной окружности треугольника
.
а
–
биссектриса внутреннего угла. Таким
образом,
–
точка пересечения биссектрис внешнего
и внутреннего углов треугольника, то
есть
–
центр вневписанной окружности треугольника
.
