Часть I. Определение симедианы
1.1 Определения и их эквивалентность
А) Рассмотрим треугольник АВС, его медиану АМ и биссектрису AL. Пусть прямая AN симметрична прямой АМ относительно прямой AL (N лежит на отрезке BC). Тогда отрезок AN называется симедианой треугольника АВС.
Б
.
Рассмотрим
вспомогательное утверждение: пусть
прямые
и
симметричны
относительно биссектрисы угла
треугольника
(точки
и
лежат
на прямой
),
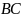тогда
.
Доказательство:
Пусть
Запишем
теорему синусов:
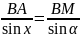(для
△BAM);
(для
△
);
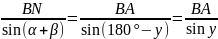(для
△
);
(для
△
)
Таким
образом,
.
Следовательно,
,
что и требовалось.
Теперь докажем эквивалентность двух определений.
1)
Если
– симедиана, то
следовательно,
,
что
и требовалось.
2)
Пусть
С
другой стороны, по лемме,
,
то
есть
.
Следовательно, отрезок, симметричная
относительно
является медианой. Таким образом, эти
определения эквивалентны.
1.2 Симедиана и антипараллельность
1.2.1
В
треугольнике
проведен
отрезок 
,
антипараллельный стороне
,
с концами на сторонах 
и 
соответственно.
Докажите, что отрезок 
является
симедианой треугольника т. и т. т., когда
он, пересекая
отрезок
,
делит его пополам.
Доказательство:
Рассмотрим
симметрию относительно биссектрисы
угла
.
Образы точек
и
принадлежат прямым
и
соответственно, причем полученный
отрезок параллелен прямой
.
Следовательно, его середина лежит на
медиане треугольника
тогда и только тогда, когда
–
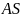симедиана (по первому
определению).
1.2.2
(Московская
математическая олимпиада
2008)
Высоты
и
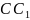остроугольного треугольника
пересекаются в точке
. Точка
– середина стороны
.
Докажите, что точка пересечения прямых,
симметричных
и
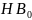относительно биссектрис углов
и
соответственно, лежит на прямой
.
Доказательство:
Заметим,
что
– отрезок, антипараллельный
.
Из задачи
№1.2.1
следует, что прямая, симметричная
относительно
проходит через середину
(точку
).
Аналогично, прямая, симметричная
,
относительно биссектрисы угла
,
проходит через точку
.
1.3 Симедиана и ортоизогональ
1.3.1 Докажите, что в неравнобедренном треугольнике одна из симедиан совпадает с высотой т. и т. т., когда этот треугольник – прямоугольный.
Доказательство:
Воспользуемся
следующим фактом: пусть
–
центр описанной окружности треугольника
,
–
ортоцентр, тогда
.
1)
Пусть
также является симедианой, тогда
(центр описанной окружности) лежит на
медиане (Так как
).
Таким образом, если
неравнобедренный треугольник, то
– середина
следовательно,
–
прямоугольный треугольник.
2)
Пусть треугольник
– прямоугольный, c
гипотенузой
и медианой
.
Заметим, что
.
Таким
образом, если провести симедиану
,
то
.Следовательно,
угол
– прямой, то есть
является ещё и высотой треугольника.
1.4 Симедиана и подобие
1.4.1
А) Окружность
проходит через точки
и
и касается прямой
,
окружность
проходит через точки
и
и касается прямой
.
Докажите, что общая хорда этих окружностей
является симедианой треугольника
.
Доказательство:
Докажем,
что
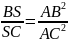(см.
второе
определение симедианы).
Заметим,
что
–
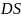биссектриса угла
,
то есть
.
Из подобия треугольников
и
(по
двум углам) получим, что
.
Следовательно,
,
что и требовалось.
Б)
(Всероссийская
олимпиада по геометрии 2008)
Пусть
– медиана треугольника
,
серединные перпендикуляры к
и
пересекают
в точках
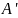и
соответственно,
прямые
и
пересекаются
в точке
.
Докажите, что
– симедиана треугольника
.
Рис. 1
Рис. 2
Доказательство:
1)
Рассмотрим
рис. 1.
То, что
лежит на серединном перпендикуляре к
равносильно
тому, что треугольник
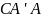– равнобедренный. Из этого следует, что
.
Проведем симедиану
(см.рис.2).
Следовательно,
.
Аналогично,
.
2)
Рассмотрим
рис. 2.
Заметим, что точка
в данном треугольнике аналогична точке
в треугольнике
из предыдущего пункта. Таким образом,
прямая
содержит симедиану треугольника
.
Что и требовалось.