17 вопрос. Линейное неоднородное уравнение 2го порядка

Структура общего решенияЛинейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x) соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения:

со спец. правой частью: f(x)=e^ax*(Pn(x)*cos(Bx)+Qn(x)sinBx)

e^2x(x*cos*3x+(x^2 -4)sin3x)

f(x)=x^2 -4x+2=e^0*x ((x^2 -4x+2)*cos0+0*sin0)

18 вопрос.Числовой ряд – это сумма членов числовой последовательности вида .Пусть мы имеем числовую последовательность a1,a2,an... , где a принад-итR,k=1,2..Приведем пример числовой последовательности: 6,3,-3/2,3/4,3/8,-3/16...

Свойства сходящихся числовых рядов.

1. Если сходится числовой ряд 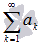 , то сходящимся будет и ряд 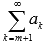 . Другими словами, сходящимся будет и ряд без первых mчленов. Если к сходящемуся числовому ряду   добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.

2. Если сходится числовой ряд   и его сумма равна S, то сходящимся будет и ряд 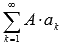 , причем 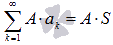 , где A – произвольная постоянная.

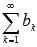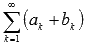3. Если сходятся числовые ряды   и  , их суммы равны A и B соответственно, то сходящимися будут ряды   и  , причем их суммы будут равны A + B и A - B соответственно.

Геометрический ряд.

Так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а₀ и знаменателем прогрессии, равным q.

Если |q| < 1, то существует предел суммы n первых членов этой прогрессии при неограниченном увеличении количества этих членов n:

В этом случае говорят о бесконечно убывающей геометрической прогрессии.

Необходимое условие сходимости ряда.

Если числовой ряд сходится, то предел его k-ого члена равен нулю: .

При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если , то ряд расходится.

С другой стороны нужно понимать, что это условие не является достаточным. То есть, выполнение равенства не говорит о сходимости числового ряда . К примеру, для гармонического ряда необходимое условие сходимости выполняется , а ряд расходится.

19 вопрос.

Знакоположительные ряды*

1.Определение:Пусть a1,a2,an.... – последовательность вещественных чисел. Числовым рядом называется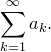 .Сумма  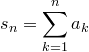 называется частной суммой ряда.

2.Достаточные признаки сравнения сходимости знакоположительных числовых рядов Если , и ряд сходится, то сходится и ряд .

Если  , и  ряд   расходится, то расходится и  ряд  .

Признаки сравнения можно сформулировать в такой форме:

Если заданы ряды  ,   и существует 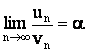    , то ряды   и   сходятся либо расходятся одновременно.

3.Интегральный признак Коши

Пусть задан ряд 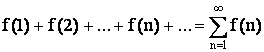 , члены которого являются значениями непрерывной, положительной и монотонно убывающей функции   на промежутке  . Тогда ряд 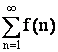  сходится, если сходится несобственный интеграл 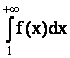 . Если же   расходится, то ряд   также будет расходящимся.

Вопрос 20! Знакочередующиеся ряды. Признак Лейбница.

Что такое знакочередующийся ряд? Это понятно или почти понятно уже из самого названия. Сразу простейший пример.

Рассмотрим ряд   и распишем его подробнее:

Знакочередование обеспечивает множитель  : если   чётное, то будет знак «плюс», если нечётное – знак «минус». На математическом жаргоне эта штуковина называется «мигалкой». Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».

В практических примерах знакочередование членов ряда может обеспечивать не только множитель  , но и его родные братья:  ,  ,  , …. Например:

Подводным камнем являются «обманки»:  ,  ,   и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном  :  ,  ,  . Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решенияфункциональных рядов.

Как исследовать знакочередующийся ряд на сходимость? Использовать признак Лейбница. Признак Лейбница: Если члены знакочередующегося ряда убывают по модулю, то ряд сходится.

Или в два пункта:

1) Ряд является знакочередующимся.

2) Члены ряда убывают по модулю. То есть,  .

Если выполнены оба условия, то ряд сходится.

Справка для тех, кто забыл, что такое модуль:

Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду  . Мысленно сотрём все знаки и посмотрим только на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначает одно и то же:

– Члены ряда без учёта знака убывают. – Члены ряда убывают по модулю. – Члены ряда убывают по абсолютной величине. – Модуль общего члена ряда стремится к нулю: 

Конец справки

Вопрос 21!

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Признак Лейбница

Для знакочередующихся рядом действует достаточный признак сходимости Лейбница.  Пусть {a_n} является числовой последовательностью, такой, что

1. a_n+1 < a_n для всех n;  2.  .

Тогда знакочередующиеся ряды 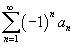  и   сходятся.

Абсолютная и условная сходимость

Ряд   называется абсолютно сходящимся, если ряд   также сходится.  Если ряд   сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.  Ряд   называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.