2.2 Примеры решения задач

Задача 1. Вычислить где― часть эллипсалежащая в квадранте.

Решение. Параметрическое задание эллипса имеет вид Поскольку рассматривается часть эллипса, лежащая в квадранте, то Поэтому, т.к.то применяя формулу (2.3), получим

Задача 2. Вычислить где― кривая, заданная уравнением

Решение. Перейдем к полярным координатам: Уравнение кривойпримет видДля вычисления интеграла применим формулу (2.5). Так както

Задача 3. Найти массу материальной кривой, заданной уравнениемгде, если ее плотность

Решение. По формуле для массы Для вычисления интеграла воспользуемся формулой (2.4). Так както

3. Поверхностные интегралы первого рода

Пусть функция, непрерывная на некоторой гладкой ограниченной поверхности. Разобьем поверхностьначастей, не имеющих общих внутренних точек, и в каждой частивыберем произвольную точкуСоставим интегральную сумму

(2.7)

где ― площадь

Пусть Если интегральная сумма (2.7) имеет предел прине зависящий от способа дробления поверхностина частии от выбора точекв них, то этот предел называется поверхностным интегралом 1-го рода от функциипо поверхностии обозначаетсят.е.

(2.8)

Если через обозначить площадь поверхности, то из формулы (2.8) следует причто

(2.9)

Если на поверхности распределена с плотностьюнекоторая масса, то

(2.10)

Координаты центра масс, статические моменты и моменты инерции материальной поверхности вычисляются по формулам, аналогичным формулам (1.5) ― (1.7).

Если поверхность задана уравнениемто вычисление поверхностного интеграла сводится к вычислению двойного интеграла по области- проекции поверхностина плоскость:

(2.11)

где Формула (2.9) для вычисления площади в этом случае принимает вид

(2.12)

Если гладкая поверхность задана параметрическими уравнениями

где функции имеют непрерывные частные производные первого порядка в замкнутой областито

(2.13)

где

(2.14)

2.4 Примеры решения задач

Задача 1. Вычислить где- часть поверхностивырезанная поверхностью

Решение. Поверхность является частью параболоида, отсеченной конусом(рисунок 2.2).

Рисунок 2.2

Поверхность однозначно проецируется на плоскостьв область― круг радиусас центром в начале координат. Уравнение окружности, которая является границейполучается, если из уравненийиисключить

Разрешая уравнение поверхностиотносительнополучаемСледовательно,Поэтому, воспользовавшись формулой (2.11), получаем

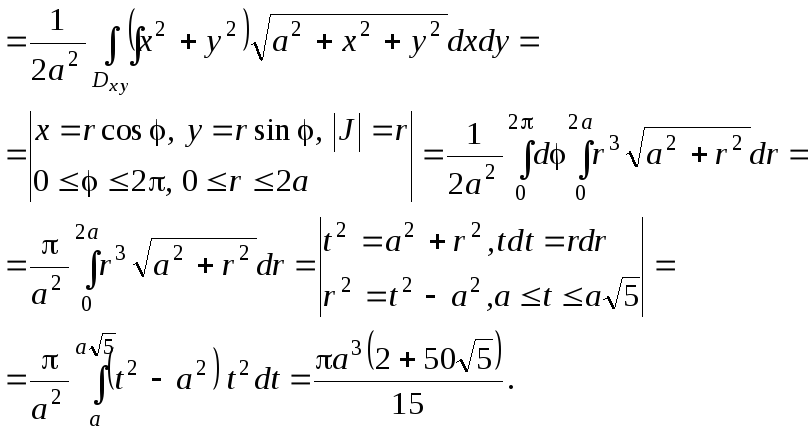
Задача 2. Найти массу поверхности сферы радиусом если ее поверхностная плотность в каждой точке равна расстоянию от этой точки до вертикального диаметра.

Решение. Взяв за начало координат центр сферы и направив ось по вертикали, получим, что расстояние от точкисферы до осиравнозначит, плотность.

Согласно формуле (2.10)

где сфера, центр которой находится в начале координат.

Для вычисления интеграла применим формулу (2.13), поэтому запишем параметрическое представление сферы

По формулам (2.14) вычислим

Следовательно,

3 Варианты заданий

Первые пять задач каждого варианта необходимо решить при следующих условиях:

1. Изменить порядок интегрирования в двойном интеграле.

2. Найти координаты центра тяжести однородной фигуры, ограниченной данными линиями.

3. Найти площадь части поверхности вырезаемой поверхностью.

4. Найти объем тела, ограниченного заданными поверхностями.

5. Найти массу тела плотности ограниченного данными поверхностями.