ТестЛюка-Лемера

^{Тестсоздаетпоследовательностьнатуральныхчисел:S}₀^,S₁^,S₂^,...,S_p-2

k

,определяемуюрекуррентнойформулойS_k+1=S²

^-2,гдеS_o

=4.Пустьр-

простоечисло.ЧислоМерсеннаМ(р)являетсяпростымтогдаитолькотогда,когда

S_p-2modM(p)≡0,т.е.остатокравен0.

Поясним,какимобразомзадаетсярядS_k.Членыпоследовательности

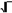
_{(натуральныечисла)можнозаписатьввидесуммстепенейнекоторых}

_{иррациональныхчисел.Пусть}

_2

_3и

_2

_{3.Докажеминдукцией}

поn,что

_2n

²n

^S_n.

Очевидно,



^S_0. Предположим, что

_2n1

_2n1

^Sn1^.

_{Возводя в квадрат обе части равенства, получаем}

_2n

2()

₂n1

²n

S²

_{n1.Поскольку}

_{1,тоследуетсоотношение}

n

n

^2²

^S2n1^2,что,поопределению,даетS.

n

Описаниеалгоритма.

1.Вводp.Еслиp<3,товыход(неудовлетворяетусловиямалгоритма).

2. Вычисление M(p)=2^p - 1 (программная реализация операции

возведениявстепеньрассмотренавприложении1).

_{3.УстановитьS=4.}

_4.Для

_{i1,p2}

_{вычислитьS=(S}²_{modM(p))-2(подоперациейmod}

подразумеваетсявзятиеостаткаотделениялевогопараметраправым).

5.ЕслиSmod(M(p)-1)0,тоM(p)являетсяпростым,иначесоставным.Выход.

Пример1.8.НеобходимопроверитьнапростотучислоM(p)=2^p-1,где

p=11-простое.

_{ЧислоМерсеннаравноM(p)=2}^p_-1=2¹¹_{-1=2047.Переменнаяциклаi}

_{(изпункта4)будетприниматьзначения}

_{i1,9.Представимшагиработы}

алгоритманаосноветрассировочнойтабл.1.8.

_{Таблица1.8.Трассировочнаятаблица}

Шаг,i	Условие: ip-2	S2modM	(S2modM)-2	Условие: SmodM0?
доцикла	-	-	4	-
1	Да:111-2	16	14	нет
2	Да:211-2	196	194	нет
3	Да:311-2	790	788	нет
4	Да:411-2	703	701	нет
5	Да:511-2	121	119	нет
6	Да:611-2	1879	1877	нет
7	Да:711-2	242	240	нет
8	Да:811-2	284	282	нет
9	Да:911-2	1738	1736	нет
10	Нет:10>11-2: Выход	-	1736	Нет→ составное

В результате получаем, что число M(p)=2¹¹⁻1=2047 являетсясоставным.

_{Пример1.9.НеобходимопроверитьнапростотучислоM(p)=2}^p_-1,где

p=13.

_{ЧислоМерсеннаравноM(p)=2}^p_-1=2¹³_{-1=8191.Переменнаяцикла}

_{i(изпункта4)будетприниматьзначения}

_{i1,11.Представимшагиработы}

алгоритманаосноветрассировочнойтабл.1.9:

_{Таблица1.9.Трассировочнаятаблица}

Шаг,i	Условие: ip-2	S2modM	(S2modM)-2	Условие: SmodM0?
доцикла	-	-	4	-
1	да:113-2	16	14	нет
2	да:213-2	196	194	нет
3	да:313-2	4872	4870	нет
4	да:413-2	3955	3953	нет
5	да:513-2	5972	5970	нет
6	да:613-2	1859	1857	нет
7	да:713-2	38	36	нет
8	да:813-2	1296	1294	нет
9	да:913-2	3472	3470	нет
10	да:1013-2	130	128	нет
11	да:1113-2	2	0	да
12	нет:12>13-2: Выход	-	0	да→простое

Врезультатеполучаем,чточислоM(p)=2¹³⁻1=8191являетсяпростым.

Вопросыдлясамопроверки.

1.ЧтотакоечислоМерсенна?

2.Еслиpявляетсясоставнымилипростым,точтоможносказатьочислеM(p)?

3.Почему,еслиpявляетсясоставным,тоM(p)-составное?

4.ПояснитесутьтестаЛюка-Лемера.

5.КакиеограничениянакладываютсянавходныезначениятестаЛюка-Лемера,втомчислесучетомпрограммнойреализациинаЭВМ?

6.Сколькоитерацийможетвыполнятьсятест?

7.ПрикакомусловиипронимаетсярешениеопростотечислаM(p)?

8.Какаяошибкаможетслучитьсяприпроверкебольшогочисланапростоту?

9.ДлякакогомаксимальногочислаpможнопроверитьпростотуM(p)спомощьюарифметики,встроеннойвЭВМ?

10.КакиематематическиеоперациииспользуютсявтестеЛюка-Лемера?