Лекция№3

Свойстваделимостицелыхчисел

ДвачислаaиbназываютсявзаимнопростымиеслиихНОД=1

(a₁,a₂,….,a_n)=НОД

(a₁,a₂)=d₁

(a₃,d₁)=d₂

…………..

(d_n-3,d_n-1)=d_n

a₁*a₂=k*d

Теоремаразложенияцелыхчисел(главнаятеоремаарифметики)Любоесоставноечислоmможнооднозначнопредставитьввидепроизведенияпростыхсомножителейp,m=p1*p2*…..*p_k

Этатеоремаимеетбольшоеприкладноезначениевкриптографии.

Обозначения:

m–составноечисло

p-простое

Составноечисломожетраскладыватьсянапростые,приэтоммогутбытьдвеформы:

1)когдавсесомножителиразные

2)когдаестькратныесомножители

Пример:m=720

Применимшкольныйалгоритмразложения–последовательноеделениенавозрастающиепростыесомножители

720 2

360 2

180 2

90 2

45 3

15 3

5 5

Кратностьуказываетсяспомощьюверхнегоиндекса720=2⁴*3²*5-

такаяформаноситназвание–каноническоеразложениенапростыесомножители.

Этопозволяетприбольшемчислекратныхсомножителейдостаточнокомпактнозаписатьразложение.

Спомощьютакого«школьного»алгоритмачислосбольшим

количествомдесятичныхзнаковможнораскладыватьгодами.

Этооднаизсложныхматематическихзадачнакоторойоснованыалгоритмышифрование/расшифрованияспомощьюоткрытогоключа.Присекретномключеданнаязадачанеиспользуется.Вообщешифрованиесоткрытымключомоснованонарядематематическисложныхзадач.Задач,длякоторыхбыстродействующиеалгоритмыпоканепридуманы.Наэтомиоснованакриптостойкость.Этакриптостойкостьноситназваниепрактическойкриптостойкости,т.к.кактолькобудутнайденыдругиебыстродействующиеалгоритмыразложение,этиалгоритмыпотеряютсвоюактуальность.Вперспективетакимвозможнымалгоритмомможетстатьалгоритмнаосновеквантовойфизики.Тамвсепроцессыидутпараллельноинезависимооттаконасколькобольшоечисловседелаетсядостаточнобыстро.

Однимизалгоритмовоснованныхнарешениесложныхматематическихзадач,являетсяалгоритмRSA.Этоталгоритммырассмотримводнойизследующихлекцийинемножкоподдругимуглом.

Применениеэтойтеоремыэто–напримердлянахождениеНОД.Т.езнаяразложение,двачисла,допустимaиbтакиечто:

Примечание:Приполучениеразногочисласомножителейможнодописатьтакназываемые«фиктивные»сомножители.н-р: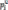

_{мыможемнайтиНОДпоформуле:}

Откаждогоразложениеберетсяпарасомножителей,выбираетсяпопоказателям.

изкаждойпарысомножителейвыбираетсясомножительсминимальнымпоказателем.

_Пример

90	2
45	3
15	3
5	5

Т.е. 720=2⁴*3²*5,

а90=2*3²*5

Беремминимальныепоказатели:

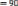
_{-т.е.число90являетсяНОД(d)чисел90и}

720.

АналогичноНОК:

-т.е.число720являетсяНОК(k)чисел90и720.

Другаясфераприложенияэтон-р:Имеемнекотороебольшоечислоиимеемегоразложениеинаосновеэтогонадонайтивсеегоделители.

Есликратностьвразложениеестьтоудобноиспользоватьопределенныйспособнахождениявсехделителей.

Вобщемслучаекогдасоставноечислораскладываетсяпоканоническойформулевседелителиможнонайтипотакойформуле(этаформулатожеобосновываетсятеоремой)

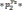
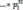-мыимеемразложение

_{…………….}

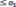
Внашемслучае(про720)

иподставляявсевозможныевариацииэтихзначениймыиполучимвседелители.

т.е.d=1,2,4,8,16…………

внашемслучаебудет30делителей

Ещеодинвариантприложенияразложения.Поразложенияможнонайтисуммувсехделителей( )

Принятообозначатьсуммувсехделителейнашегочислаакак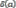

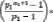
Длянашегопримераэтобудетвыглядетьтак:

Свойстваделимостицелыхчисел

Свойстваприведеныбездоказательства.

1)Свойстводистрибутивности

Пустьзаданнытринатуральныхчислаa,b,c.Еслиустановленочтоc|b(c

делитb)безостаткаивсвоюочередьb|aбезостатка,тоc|aбезостатка.

2)Пустьданыa,b,c,еслис|aиc|b,тотогдаc|(a+b)иc|(a-b)

3)Имеем3числаa₁,a₂,c.Причем(a₁,c)=1–взаимнопростыеи (a₂,c)=1,

тогда(a₁*a₂,c)=1(т.е.тожевзаимнопростые).

4)Допустиммыимеемдвамножествачисел(a₁,a₂…..а_k)=Aи(b₁,b₂…..b_k)=B.Причемдлякаждогочислаизодногомножестванайдетсявзаимнопростоечисло(a_i,b_j)=1.Тогда

^(a₁^*a₂^*…..*а_k^),(b₁^*b₂^*…..*b_k^{)=1.Т.е.(A,B)=1/}

4’)Частныйслучайеслиданыa^kиb^k.Если(a,b)=1то(a^k,b^k)=1и(a^k,b^m)=1

4”)Естьдванатуральныхчисла(a₁,a₂)=1иестьнекотороечислоb(тоженатуральное).Пустьa₁|bиa₂|b,тогдаa₁a₂|b

5)Пусть(a₁,a₂…..а_k)=d

Тогда(a₁/d,a₂/d…..а_k/d)=1

6)Пустьимееммножествочисел(a₁,a₂…..а_k)=d(нашлиНОД)ипустьмыимеемb>0,такоечтоb|d,тогда(a₁/b,a₂/b…..а_k/b)=d/b–НОДмножества.

7)Пусть(a,b)=1иестьc,тогдаеслиb|ac,тоb|c.

8)Пусть(a,b)=1,иестьс.Тогдаеслиa|c,b|c,тоab|c

_{9)Еслиp-простоечислоp|ab,толибоp|aлибоp|b.}

_{Свойствапростыхчисел:}

Простыечисла

1) -каноническоеразложение

2)минимальныйделительчислаm(m-целое)являетсяпростымчислом.Этосвойствоявляетсяпрямымследствиемизглавнойтеоремыарифметики.

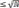3)припоследовательномнахождениевсехпростыхчисел,наосинатуральныхчисел,1,2,3,5…Nтопритакомспособедостаточнорассмотреть(дойтидо)простоечисло .

Т.е.этогодостаточно,чтобыпритакомпоследовательномспособеполучитьвсепростыечисланаэтойоси.ПримеромданногоспособаявляетсяРешетоЭратосфена.

4)Еслимыимеемпроизведениедвухнатуральныхчиселa*bиимеемпростоечислоp,причемтакоечтоp|a*b,тогдаp|aилиp|b.(этосвойствоиграетнепоследнююрольприанализекриптоалгоритмов)

Этисвойстваиспользуютсявтеорииделимостицелыхчисел.

Атеперьвыяснимвчемзаключаетсясложностьполученияразложения.Еслимыпосмотримнаосикакрасположеныпростыечисла,товыяснимчтооказываетсядосихпорненайденазакономерностьихрасположения.С

однойстороныонирасположенынеслучайно,асдругойстороныненайденоформулыспомощьюкоторойможнобылобыполучитьвсюпоследовательностьтакихчисел.

Последовательностьпростыхчиселбесконечна.ЭтодоказаноещеЕвклидом.Пыталисьвыразитьпоследовательностьпростыхчиселспомощьюцелочисленныхполиномов,нобылодоказаноещев19векечтосихпомощьюнельзяполучитьвсюбесконечнуюпоследовательностьчисел.

Отдельныеподмножестваэтойпоследовательностиполучитьможно.н-р:x²-

30+40.еслииксупредаватьзначения1,2,3…40,тополучим40простыхчисел.Естьформулыкоторыедаютбольшиепомощностиподмножества,новсе-такиэтоотдельныеподмножества.

Теперьрассмотримпорядокрасположенияпростыхчисел.Всетакикакие-тозакономерностиесть,рядтакназываемыхасимптотическихзакономерностей: