ФункцияМебиуса

ФункцияМебиусаслужитхарактеристикойканоническогоразложения.

?(d)–обозначение

Характеристикиканоническогоразложения:

1)кратность

2)четность

3)нечетность

(числосомножителейможетбытьчетнымилинечетным)

ФункцияМебиусаиотражаетэтихарактеристики,онапринимаеттризначения:0,1,-1.

1,приd=1,

?(d)=(-1)^к,еслиdпроизведениекпростыхчисел,

0,Еслиdделитсянаквадратнекоторогоростогочисла.

Еслихотябыодинсомножительявляетсякратным,тоФункция

Мебиусапринимаетзначение0.

Есличислочленовчетное,тоФункцияМебиусапринимаетзначение1

Есличислочленовнечетное,тоФункцияМебиусапринимаетзначение

-1.

Причемхарактеристикакратностьимеетбольшийприоритет.Т.е.есликратноеинечетное,то?(d)=0.

Пример.

?(1)=1

?(2)=1

?(3)=-1

?(4)=0

?(5)=-1

?(6)=1

…….

НаосновеФункцииМебиусаможнонайтиФункциюЭйлера(третьяформула).

ЭтатакназываемаясвязьФункцииМебиусаиФункцииЭйлера.

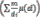III)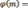 ,суммированиевыполняетсяповсемделителямd_i|m.

Заданочислоm

1)Находимвседелителиdi|m

_{2)находимчисла}

_{делителя.}

3)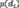 -находимфункциюМебиусадлякаждогозначения

ВконцемыиполучаемзначениефункцииЭйлера.Пример:m=18

1)d_i=1,2,3,6,9,18

2)числа =18,9,6,2,1

3)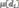 =1,(-1),(-1),(-1),(1),0,0

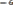_{Витогеполучаем:}

Числоваяфункция

Этофункцияустанавливающаяцелуючастьотнекоторогорациональногочисла

[a]–обозначение

можетбытькакположительное,такиотрицательноечисло.

[3,5]=3.

Примерприложенияэтойфункциивкриптографии:

Разложениефакториалов.Дляразложениянапростыесомножителичисел.Пример:6!=1*2*3*4*5*6=720

или1000!–егомыразложитьнасомножителинесможем(вычисляя).Номыможемспомощьюэтойформулыразложитьневычисляя.

1000!=p₁*p₂*…*p_l

Допустимзадано6!=1*2*3*4*5*6Дляэтогослучаямызнаем,чтосомножителинепревышаютсамочисло6.

имыможемвоспользоватьсяформулой.

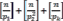длязаданногочислаn,факториалкоторогомыхотимразложитьневычисляяфакториалn!:

Позволяетустановитькратностьфиксированногосомножителя.,

_{Пример.Определимкратностьдвойкивчисле6!=720.}

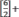
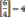Т.е.двойкавстречается4раза.

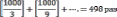Мынераскладываяфакториал,можемпроверитьвсесомножителии.т.д.Допустимсколькоразсомножитель3входитв1000!

Лекция№7

Возведениенатуральныхчиселпомодулювбольшиестепени

1.ПриложениефункцийЭйлера

длявозведениенатуральныхчиселпомодулювбольшиестепени

ФункцияЭйлераможетбытьиспользованадлявозведениебольшихчиселвбольшуюстепеньпомодулю.

Имеетсяцелоечислоавозводимеговцелоечислохитребуетсявзятьмодуль–тоженекотороецелоечислоmиполучитьостатокотэтогочислаr.

a^xmodmr

ПрименениетеоремыЭйлерапозволяетнамдостаточнобыстровозводитьбольшиечиславбольшуюстепень

Приопределенномнавыкенабумагеможносделатьгораздобыстрее,чемнакомпьютере.

ПримерПустьдано:a=2х=5432675

m=p=13 ТеоремаЭйлера^{a(m)modm1}

m-целое.a-взаимнопростоесm

ТеоремаЭйлераутверждает,чтоостатокбудетравен1

Еслиmпростое,тоф(р)=p-1

_a^p1_1modp

1)НаходимфункциюЭйлерадлячислаm=p=13,т.е. ф(р)=p-1=12.

2)ЧислохпредставляемчерехфункциюЭйлерах=5432675=qф(р)+r=452722*12+11=4352722+11

_{3)Вычисляем}

₍₂4352722*1211_)mod13(24352722*12_*211_)mod13

2048

₌

(2^4352722*12mod13)(2^11mod13)mod13

₍₂4352722*1211_)mod137

Здесьсомножитель(2^435272*12)mod13потеоремеЭйлераравен1.

Рассмотримобщийслучай

СначаланужновычислитьзначениефункцииЭйлерадлячислаm

(a^(m))modm

а=317

x=259

_{m=15,ф(15)=8}

^{317259mod15y}

x=259=8*32+3

Вычисляем:(а^8*32+3)mod15=(а^8*32)mod15(а³)mod15=

(317^3mod15)2^3mod158

_Ответ:8

_{Учитываем,что сомножитель(а}^8*32_{)mod15и 317mod15=2.}