1.3. Механические свойства горных пород при простых видах деформации

Механические свойства горных пород - свойства, которые определяют поведение горных пород при их деформировании.

Понятие о деформациях во второй половине ХIX века ввел Л.Навье.

Деформацией называется относительное смещение частиц материального тела (породы), при котором не нарушается сплошность тела.

Деформации развиваются вследствие действия напряжений.

Понятие напряжений в теорию прочности ввел O.Коши, который дал определение, что напряжения – средняя интенсивность силового воздействия, приходящаяся на единицу площади разрушаемого тела [36, 37].

Исследованиями различных видов деформаций в зависимости от вызывающих их напряжений занимается реология.

• Реология (от греч. rheos – течение, поток) – наука о деформациях и текучести веществ.

Реология охватывает весь спектр материалов между телом Р. Гука и ньютоновской жидкостью. Если с технологической и физической точек зрения различие между твердыми телами и жидкостями значительно, то реология не считает это различие существенным. На основании её положений бетон можно рассматривать как жидкость с периодом релаксации ~10⁶ с, а воду – как твердое тело со временем релаксации ~10^-10 с [26].

• Релаксация (лат. relaxation – ослабление, уменьшение) – процесс изменения напряжений в теле при постоянном его деформировании под действием внешних сил.

В случае быстрой деформации жидкости ведут себя как истинно упругие тела, подчиняясь законам теории упругости Р. Гука. Например, при быстрых воздействиях (прострел пулей) струя воды раскалывается хрупко, как стеклянная нить. При высокой скорости перемещения по воде можно скользить как по льду.

Таблица 1.4

Реологические модели для исследования поведения горных пород

при деформировании

Тип	Модель	Характеристика
I. Основные
Жесткий	Эвклида	Практически не деформируются (ε = 0). Происходит хрупкое разрушение в виде разрыва внутренних связей при напряжении σ, превышающем предел прочности
Упругий	Гука	Разрыв связей происходит после упругих деформаций. Закон деформирования: , σ – напряжения; E – модуль упругости; ε – относительная деформация
Пластичный	Кулона	Смещению частей деформированного тела противодействует внутреннее трение, которое и обуславливает сопротивление пластическому деформированию
Вязкий	Ньютона	Смещение частиц происходит с постоянной скоростью вследствие деформируемости связей. σ = ηε, η – вязкость
II. Производные
Упруго-пластичный	Сен-Венана	Деформирование до предела пропорциональности происходит упруго, а затем по схеме пластичного деформирования
Упруго-вязкий	Кельвина-Максвелла	Деформации связей как упругие, так и вязкие
Упруго-вязко-пластичный	Шведова	Сопротивление происходит в результате деформируемости вязких связей и внутреннего трения по плоскостям смещения и разрыва после преодоления упругих связей
Вязко-пластичный	Бингама	Сопротивление происходит в результате деформируемости вязких связей и внутреннего трения по плоскостям смещения и разрыва

И, наоборот, твердые тела ведут себя, как жидкости при медленной деформации – деформационное течение пород за длительный период времени.

Основные теоретические реологические модели, отражающие поведение горных пород при деформировании, приведены в табл. 1.4 [37].

Основные виды деформации горных пород: сжатие, растяжение и изгиб.

Деформации могут быть упругими - обратимыми и необратимыми - пластическими или хрупкого разрушения. Пластические деформации определяются степенью пластичности. Разрушение же наступает при преодолении предела прочности на завершающей стадии необратимых деформаций.

Большое разнообразие горных пород, изменчивость их состава и свойств вызывают различную реакцию со стороны породы на воздействующую силу. С точки зрения деформируемости диапазон поведения горных пород очень широк: от микрон до миллиметров.

Физической причиной разнообразия деформируемости пород является различие внутренних связей, под которыми понимают совокупность сил взаимодействия между частицами и структурными агрегатами.

Для характеристики деформационных свойств твердого тела в упругой области используются:

• модуль (деформации) упругости Е (модуль Юнга);

• коэффициент поперечного расширения μ (коэффициент Пуассона – изменяется в пределах 0,01-0,4);

• модуль сдвига G;

• модуль объемного сжатия К.

Модуль упругости E по закону Р. Гука связывает напряжение σ и деформацию ε зависимостью σ = ε × Е.

Коэффициент Пуассона μ отражает продольную ε_пр и поперечную ε_поп деформации зависимостью ε_поп = - μ × ε_пр .

Модуль сдвига G связывает касательные напряжения τ с деформацией сдвига ξ зависимостью τ = ξ × G.

Модуль объемного сжатия К – гидростатическое давление p₀ с относительно объемной деформацией ε₀ связан зависимостью р₀ = - К × ε₀.

Показатели деформационных свойств в пределах действия закона Р. Гука связаны следующими зависимостями:

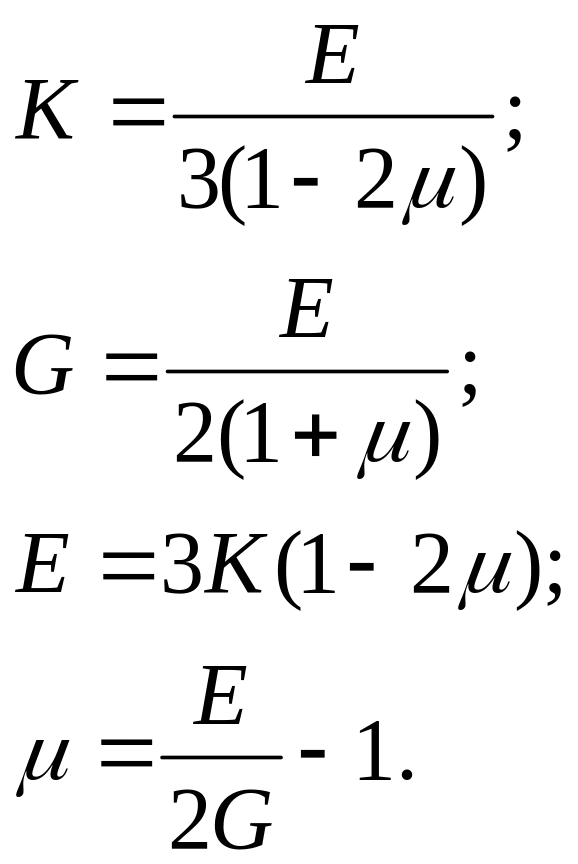(1.4)

Горные породы вследствие их сложного строения относятся к анизотропным телам, поэтому упругие константы зависят от направления деформации.

Полидисперсное строение горных пород обуславливает появление в них при нагружении необратимых деформаций даже при сохранении линейного характера деформаций. Это предопределено межкристаллическими сдвигами, уменьшением пористости пород. При некотором увеличении числа циклов нагружений остаточные деформации в породе снижаются, а упругие свойства возрастают. Поэтому различают:

- модуль упругости при однократном нагружении Е;

- модуль упругости, получаемый после исключения остаточных деформаций путем многократного нагружения E_н;

- модуль упругости, получаемый при динамическом нагружении Е_д.

Экспериментально установлено, что Е= (0,7-0,8)Е_н=(0,3-0,5)Е_д.

Величины модулей упругости, полученные при растяжении (Е_р), изгибе (Е_и) и сжатии (Е_с), также будут различны: Е_и=(0,25-0,35)Е_с = (1,2-1,3) Е_р.

Модуль упругости при сжатии (в МПа) для некоторых пород:

гранит – 60 000; базальт – 97 000; известняк – 85 000; песчаник – 45 000; глинистый сланец – 20 000; глина – 300.

Прочность горной породы определяется значениями критических напряжений, которые приводят к её разрушению.

Основными прочностными характеристиками горных пород являются:

σ_сж - предел прочности на сжатие, Па;

σ_и - предел прочности на изгиб, Па;

σ_р - предел прочности на растяжение, Па.

Для горных пород обычно выполняется условие σ_сж> σ_и> σ_р . Например, для горных пород отношение пределов на сжатие и растяжение может составлять 10-20 раз: гранит – 141 МПа/11 МПа; порфирит 224/18; известняк 28/3; песчаник 164/7.

Условие прочности твердого тела (горной породы) установлено Ш. Кулоном. Оно базируется на том, что разрушение горных пород при действии на них сжимающих нагрузок происходит или в результате сдвига одних частей относительно других, или вследствие отрыва этих частей друг от друга, т.к. предельные касательные напряжения и напряжения отрыва значительно меньше сжимающих.

Теория Кулона развивает критерий прочности, введенный Трèски (1868 г.), согласно которому разрушение наступает при достижении касательными напряжениями некоторого максимального значения τ_max. Эта теория хорошо согласуется с условиями разрушения в случае одноосного сжатия или растяжения, при которых τ_max = 0,5 σ, где σ – нормальное напряжение [37].

Критерий Кулона устанавливает связь касательных напряжений с внутренним трением, возникающем при разрыве связей в разрушаемом материале.

При сдвиге на прочность породы оказывают значительное влияние силы внутреннего трения, которые возрастают от действия нормальных к плоскости сдвига напряжений сжатия.

С ила Q, сдвигающая часть скальной породы относительно другой, преодолевает сопротивление сил сцепления T и силы трения F = μ_о × N, т.е.

Q=T + μ_оN,

где μ_о – коэффициент внутреннего трения; N – сила, нормальная к плоскости сколь-жения.

Разделив все члены уравнения на площадь сдвига, можно получить напряжение сдвига, характеризующее прочность твердой породы:

τ = τ₀ + μ_оσ, (1.5)

где τ₀ – удельная сила сцепления;

σ – нормальное напряжение;

μ_о = tgφ, где φ – угол внутреннего трения.

Условие прочности Кулона хорошо объясняет высокую прочность горной породы при вдавливании в неё резца при бурении, т.к. в этом случае порода находится в напряженном состоянии, близком к всестороннему сжатию. Возникающие в этом случае высокие напряжения сжатия увеличивают силы внутреннего трения.

Характеристики τ_о и μ_о = tgφ, входящие в условие прочности, могут быть найдены экспериментально.

Критерий прочности Кулона (1.5) на рис.1.4 изображен в координатах касательных и нормальных напряжений (τ, σ). Линия АР, определяется как касательная к предельному кругу О.Мора, радиус которого τ_max = 0,5(σ₁ – σ₂), где σ₁,σ₂ – наибольшее и наименьшее нормальные напряжения в породе. Угол наклона касательной АР к оси напряжений φ задает угол внутреннего трения и позволяет определить коэффициент внутреннего трения

μ_о=tgφ = .

Из построения на рис. 1.4 видно, что предельное состояние, соответствующее точке Р, возникает при τ_p<τ_max и при некотором нормальном напряжении σ_р.

На основании теории прочности О. Мора [37], предложенной в 1900 году, рассчитывается интенсивность сил сцепления τ_о при одноосных сжатии σ_cж и растяжении σ_р:

Совместное решение приведенных уравнений дает следующую формулу:

при

Установлено, что для различных пород отношение η может находиться в пределах 6-80.

Анализ приведенных зависимостей показывает, что интенсивность сил сцепления τ_о практически равна пределу прочности при растяжении σ_р.

О величине прочности горных пород при растяжении, сдвиге и изгибе, выраженной в долях от предела прочности на сжатие σ_сж, можно составить представление по данным табл. 1.5 [39].

Таблица 1.5

Горная порода	Растяжение	Изгиб	Сдвиг
Граниты	0,02–0,04	0,08	0,09
Песчаники	0,02–0,05	0,06–0,2	0,1–0,12
Известняки	0,01–0,04	0,08–0,1	0,15

Данные, приведенные в табл. 1.5, показывают, что чем больше роль растягивающих напряжений при нагружении горной породы, тем эффективнее должно происходить её разрушение [26, 36, 37, 39].

Для горных пород, находящихся в сложном напряженном состоянии, т.е. испытывающих различные виды напряжений, предельные напряжения могут рассчитываться по методике на основании теории О. Мора.

С огласно теории О. Мора, уже использованной при построении диаграммы проч-ности на рис.1.4, по значениям напряже-ний можно выстро-ить предельную кри-вую, которая ограни-чивает область безопасных состо-яний и позволяет получить значение предельного касса-тельного напря-жения, при котором наступает разруше-ние. Таким образом, с помощью критерия О.Мора оценивается поведение горной породы при объем-ном напряженном состоянии на основании простых видов пределов прочности.

Паспортом прочности горной породы является кривая, огибающая предельные круги Мора в координатах нормальных σ и касательных τ напряжений (рис. 1.5). Предельный круг Мора соответствует предельному состоянию породы, достигаемому при данном соотношении наибольшего σ_max и наименьшего σ_min главных нормальных напряжений, и имеет радиус с координатами центра .

На рис. 1.5 приведены наиболее характерные круги Мора, огибающая их кривая и обозначены основные параметры, определяемые по паспорту прочности:

- предельное сопротивление срезу τ₀ (сцепление) при отсутствии нормальных напряжений и угол внутреннего трения φ;

- условное сцепление τ_с при различных напряжениях σ, τ и соответствующий угол внутреннего трения φ.

Паспорт прочности по данным определения пределов прочности при объемном сжатии, одноосном растяжении и сжатии.

Для построения паспорта прочности используют результаты определения пределов прочности при объемном сжатии σ_сж не менее, чем при трех различных значениях бокового давления p.

По совокупности парных значений σ_сж=σ_max и р = σ_min строят полуокружность радиуса 0,5(σ_сж – р) с координатами центра [0,5(σ_сж + р); 0;].

Далее добавляются полуокружности с радиусами 0,5 σ_р и 0,5σ_сж с координатами центров ( - 0,5 σ_р; 0) и (0,5 σ_сж; 0), где σ_р – предел прочности при одноосном растяжении по ГОСТ 21153.3-85; σ_сж – предел прочности при одноосном сжатии по ГОСТ 21153.3-85.

После построения полуокружностей проводят плавную кривую, огибающую все пять (или более) полуокружностей (рис. 1.5), с которой снимают постоянные и переменные параметры сцепления С и угла внутреннего трения φ.

Пластические свойства горных пород характеризуются коэффициентом пластичности К_пл и коэффициентом внутреннего трения в деформируемых слоях породы tg φ.

Угол внутреннего трения можно определить из нижеследующей зависимости на основании экспериментальных данных [26]:

, (1.6)

где - удельная сила сцепления;

σ_сж и σ_р - соответственно пределы прочности породы на сжатие и растяжение.

Угол внутреннего трения в породах наиболее часто находится в пределах 20÷60⁰ и уменьшается с увеличением содержания в породе мелких фракций и минералов, способствующих взаимному скольжению одной части породы относительно другой (например, монтмориллонита в осадочных породах).

В табл. 1.6 приведены значения силы сцепления и угла внутреннего трения некоторых горных пород [26].

Таблица 1.6

Величины силы сцепления и угла внутреннего трения ряда горных пород

Порода	τ0, МПа	φ, градус
Уголь Аргиллит Алевролит Диорит Роговик Сиенит порфировый Базальт пикритовый	4,6-10 18-23 23-26 68 85 45 27	35-37 33-34 27-32 33 35 31,5 34

При деформировании породы наблюдаются следующие стадии: I – стадия упрочнения и закрытия имеющихся трещин, порового пространства и дефектов, суммарный размер которых в линейном выражении можно оценить величиной ε_п (рис. 1.6, а); II – стадия упругого деформирования; III - стадия зарождения и развития новых трещин; IV – стадия разветвления и слияния трещин, диспергирование мате-риала, приводящее к окончательному разру-шению (рис. 1.6).

П ри нагружении горной породы проис-ходит изменение объема образца (см. график на рис.1.6,б). В завершающей стадии деформирования образец увеличивается в объеме за счет разрыхления в зоне интенсивного трещинообразования. В начальный же момент нагружения объем образца существенно уменьшается за счет сжатия и смыкания имеющихся в породе трещин.

На процесс разрушения горной породы значительное влияние оказывают пористость и трещиноватость. Пористость и трещиноватость влияют на прочность породы, упругость, коэффициент Пуассона. Так, например, у микроклиновых гранитов при увеличении пористости и трещиноватости с 0,6 до 1% предел прочности на сжатие снижается с 240 МПа до 180 МПа, а при увеличении пористости до 3% снижается и составляет 110 МПа [26].

С увеличением пористости снижается модуль упругости, а коэффициент Пуассона, согласно данным из [26], может снижаться при малых значениях пористости и увеличиваться при более высоких значениях порового пространства.

В еличина пористости тесно связана с вещественным составом горных пород, с размерами, формой и упаковкой зёрен породы. В осадочных породах пористость может достигать 35% объема породы, в вулканогенно-осадочных (туфопесчаники, туффиты) и метаморфических породах – 5-20%, в магматических породах – не более 5%.

Пористость горных пород определяет водо- и газопроницаемость горных пород. Слоистым породам присуща анизотропия водопроницаемости: водопроницаемость вдоль напластования больше, чем перпендикулярно к нему [26].

Таким образом, для анизотропных горных пород характерна и определенная ориентировка пористого пространства.

На рис. 1.7 приведена фотография забоя скважины пробуренной в блоке анизотропного туфо-дацита [21]. Забой после бурения и распиловки блока пропитан керосином. Сплошной линией и штриховкой уточнен контур забоя, штриховой линией – зона распространения керосина по породе. Форма распространения керосина по породе показывает преимущественное распространение пористости вдоль слоев породы.

Ориентировка пористости вдоль текстурных элементов породы определяет её повышенную деформируемость в направлении перпендикулярно слоистости, сланцеватости и, таким образом, может влиять на процессы разрушения анизотропной породы, определяя степень неравномерности и асимметрию объемов деформации и скалывания. Проникновение бурового раствора в направлении пористости (слоистости) также существенно влияет на эффективность разрушения породы, определяя некоторую асимметрию разрушающего действия бурового инструмента на породу при бурении [21].

Современные представления о механике разрушения горных пород основываются на таких основных теоретических положениях, как:

- критерий прочности А. Гриффитса о влиянии дефектов (трещин) на прочность твердых тел;

- опыты, модифицирующие теорию А. Гриффитса и утверждающие, что при возрастании сжимающих напряжений трещины А. Гриффитса должны закрываться, вследствие чего развивается трение по поверхности образованного контакта, а не рост трещины [36,37];

- гипотеза об эффективных растягивающих напряжениях, которые вызваны сжимающей нагрузкой [36].

Названные теории, если их рассматривать в совокупности, позволяют составить достаточно емкое и продуктивное представление о процессах разрушения горных пород при механическом их разрушении.