- •1. Алгоритм и его характеристики
- •2. Вычислимые функции и их графики
- •3.Разрешимые и перечислимые множества. Критерий разрешимости множества
- •4.Рекурсивные функции и операторы. Примеры
- •5. Машина Тьюринга и её программа. Машина Тьюринга как алгоритм
- •6. Эффективная нумерация машин Тьюринга
- •7. Неразрешимые алгоритмические проблемы
- •8. Детерминированные конечные автоматы и их работа. Диаграмма и функция переходов. Расширенная функция переходов. Язык дка
- •9. Недетерминированные конечные автоматы и их работа. Диаграмма и отношение переходов. Язык нка
- •10. Недетерминированные конечные автоматы с ε-переходами и их работа. Язык ε-нка
- •11. Языки. Операции над языками
- •12. Регулярные выражения и их свойства. Язык регулярного выражения
- •13. Регулярные выражения и дка
- •14. Свойства регулярных языков. Лемма о накачке. Замкнутость регулярных языков
- •15. Контекстно-свободные грамматики, порождения цепочек, язык грамматики
- •16. Замкнутость и разрешимость кс-языков
- •17. Полезные, порождающие и достижимые символы кс – грамматики. Нормальная форма Хомского кс-грамматики
- •18. Приведение кс-грамматики (контекстно-свободной) к нфх - грамматике (нормальной форме Хомского)
- •19. Автоматы с магазинной памятью и их работа. Конфигурация мп-автомата и его язык, вычисление.
- •21. Эффективная нумерация машин Тьюринга. Язык диагонализации и универсальный язык. Эффективная нумерация машин Тьюринга
- •22. Рекурсивный и рекурсивно-перечислимые языки. Иерархия языков по Хомскому
- •23. Временная сложность машин Тьюринга. Классы p и np языков и связь между ними
6. Эффективная нумерация машин Тьюринга
Q=
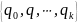 – алфавит состояний. A=
– алфавит состояний. A=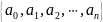
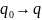 (обозн.)
a0
(обозн.)
a0
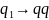 a1
a1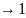
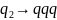 a2
a2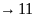
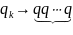 ai
ai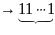
k+1 i
Машину
можем закодировать словом, имеющим
максимально 4 различных символа: x=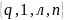
Т(i,
j) : qi
aj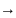 qk
am
x
qk
am
x
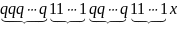 – слово
– слово
i+1 j k+1 m
Каждая команда кодируется словом вида:
qi+1
1j
qk+1
1m
x /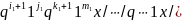
Любую машину Тьюринга мы можем закодировать таким словом, которое состоит из конечного числа символов.
Выбираем все слова, состоящие из 1-го символа и номеруем. Затем слова, содержащие 2 символа и т.д.
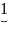
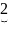
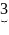
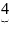
1…k k+1
k1
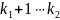
Причём однобуквенных и двубуквенных слов нет, также как и 3-х буквенных. Число машин Тьюринга не более чем счетное.
7. Неразрешимые алгоритмические проблемы
Машина Тьюринга – это алгоритм, который позволяет алгоритмически вычислять значение функции. Машина Тьюринга перерабатывает слово в слово того же алфавита.
Таким образом, так поставленная задача представляет собой алгоритмическую проблему: проблема вычисления некоторой заданной функции в некотором алфавите.
Какие функции можно вычислять с помощью машины Тьюринга? Ответ даёт тезис Тьюринга. Тезис: алгоритм для нахождения значения функции, заданной в некотором алфавите существует эта функция вычислима по Тьюрингу (т.е. существует машина, которая её вычисляет).
Класс алгоритмически вычислимых функций совпадает с классом функций, вычислимых по Тьюрингу.
Алгоритмическая проблема - проблема, в которой требуется найти единый метод (алгоритм) для решения бесконечного числа задач заданного класса.
Можно ли решить все эти проблемы алгоритмически?
Если мы вычисляем значение функции, определённой на словах этого алфавита и со значениями того же алфавита, то сколько таких функций существует? Их более, чем счётное множество. Но машина Тьюринга - не более, чем счётное множество, следовательно, есть функция, которая не вычислима по Тьюрингу.
Пример неразрешимой алгоритмически задачи – функция, которую нельзя вычислить с помощью машины Тьюринга.
Построим такую функцию:
φ(α)=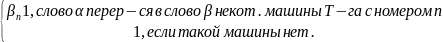
Теорем.
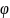 (
(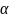 )
нельзя вычислить с помощью машины Т-га.
)
нельзя вычислить с помощью машины Т-га.
Док-во:
Допустим,
такая машина есть, которая вычисляет
и получает φ(α) =
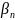 ,
а должна в
,
а должна в
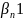 ,
а
,
а
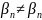 1.
1.
Задача алгоритмически неразрешима, но отсюда не следует, что задача вообще неразрешима.
Проблема самораспознавания тоже неразрешима: если вместо слова поставить слово, задающее машину, то она его не распознает.
8. Детерминированные конечные автоматы и их работа. Диаграмма и функция переходов. Расширенная функция переходов. Язык дка
Теория автоматов изучает абстрактные вычислительные устройства (машины).
Простейшие из таких вычислительных устройств называются конечными автоматами. Основной их характеристикой является то, что они являются моделью не всего программного обеспечения, а какой-то его части. Их особенностью является то, что в каждый момент они могут находиться только в одном из конечного числа состояний. Назначением каждого состояния - запоминание определенного момента истории системы.
Каждому автомату нужен алфавит. Алфавит – любое конечное множество. Элементы этого множества называются символами алфавита.
Опр. Цепочкой (словом) в данном алфавите называется конечная последовательность символов этого алфавита.
 -
пустая цепочка (цепочка, которая не
содержит ни одного символа). Пустое
слово принадлежит любому алфавиту.
-
пустая цепочка (цепочка, которая не
содержит ни одного символа). Пустое
слово принадлежит любому алфавиту.
Если
цепочка непустая, например, w
= a1a2a3
ak,
то возникает понятие длины цепочки
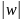 -
число символов в ней.
=k.
-
число символов в ней.
=k.
Пусть Σ – алфавит.
Опр. Степень алфавита – множество цепочек алфавита Σ длины k.
Σk = {w \ |w| = k}
Σ0 = {ε}
Σ1 = {0, 1}
Σ1 = {0, 1} ≠ Σ, Σ – множество элементов, Σ1 – множество однобуквенных слов.
Опр. Σ* - множество всех слов данного алфавита.
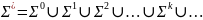
Σ+ - множество собственных слов не нулевой длины.
Σ+
=
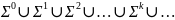
Σ*
=
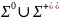
Над множеством слов данного алфавита можно производить некоторые действия:
x = a1a2a3 ak, y = b1b2b3 bl.
Опр. x∙y = xy – конкатенация цепочек х и у. Это цепочка, полученная ху = a1a2a3 akb1b2b3 bl.
ху ≠ ух – конкатенация цепочек ху не совпадает с конкатенацией цепочек ух.
хх = хх или εх = хε
Когда строим слова, не обязательно использовать все символы алфавита.
Опр.
Множество цепочек алфавита
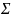 ,
каждая из которых принадлежит
,
каждая из которых принадлежит
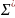 (множество
всех слов данного алфавита), называется
языком над этим алфавитом.
(множество
всех слов данного алфавита), называется
языком над этим алфавитом.
L(Σ)
= {w\ w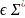 }
}
Если
L – некоторый язык над
каким-то алфавитом Σ, то L
язык над
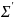 ,
где Σ
,
где Σ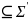 ,
т.к. если мы расширяем язык Σ, то слова
Σ будут и словами Σ’.
,
т.к. если мы расширяем язык Σ, то слова
Σ будут и словами Σ’.
Язык – это какое-то подмножество Σ.
Как задается язык?
1. язык можно задать, перечислив все его слова (если язык небольшой).
2. задать это множество с помощью характеристического свойства (регулярное выражение).
Опр.
Есть некоторое конечное множество Q
=
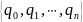 ,
которое называется множеством состояний
автомата, его элементы - состояния.
,
которое называется множеством состояний
автомата, его элементы - состояния.
Опр.
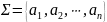 - конечное множество символов.
- конечное множество символов.
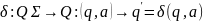 - функция переходов состояний автомата.
- функция переходов состояний автомата.
Одно из состояний этого автомата называется начальным q1 Q.
И есть некоторое подмножество состояний, заключительные состояния F⊆Q.
Опр.
Детерминированным конечным автоматом
называется упорядоченная пятерка A=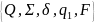 .
.
Автомат читает слова алфавита Σ. Прочитав цепочку (слово) он может попасть в одно из состояний множества F, а может и не попасть в одно из состояний F. Если автомат попадает в одно из заключительных состояний, то говорят, что автомат допускает эту цепочку, если не попадает - не допускает.
Опр. Язык автомата - это множество цепочек, которые допускает этот автомат.
Как автомат читает цепочку?
w = a1,a2,a3, ak ; q1 .
В состоянии q1 он воспринимает 1-й символ (q1, a1)
δ(q1, a1) = q2.
В состоянии q2 автомат читает (q2, a2)
δ(q2, a2) = q3 δ(qk , ak) = qk+1 F если допускается, то цепочка принадлежит языку автомата.
Как задается функция переходов δ?
1). Таблично
|
|
q2 |
|
|
qm |
a1 |
q q11 |
q12 |
q13 |
|
|
a2 |
q21 |
q22 |
q23 |
|
|
a3 |
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
|
q1 – стартовое состояние
- заключительное состояние
2). Графическое задание
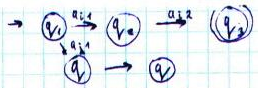
Множество цепочек, допускаемых данным автоматом, образуют язык автомата.
Опр. Расширенная функция перехода – функция, определённая на паре состояний цепочки и каждой паре состояний ставится в соответствие состояние цепочки.
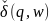 – расширенная функция.
– расширенная функция.
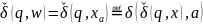
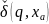 – оторвал последний символ цепочки.
– оторвал последний символ цепочки.
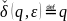 – если на пустом слове функция не
меняется.
– если на пустом слове функция не
меняется.
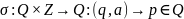 .
Автомат в состоянии q
читает а, то он переходит в состояние
р.
.
Автомат в состоянии q
читает а, то он переходит в состояние
р.
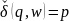 .
Если в состоянии q он
читает цепочку, то переходит в р.
.
Если в состоянии q он
читает цепочку, то переходит в р.
Опр.
Если А – ДКА, то L(A)
= {w\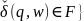 .
.
Опр. Если L – язык является языком ДКА, то он называется регулярным.

 q1
q1