2. Основные правила дифференцирования.
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
[2]
[3]
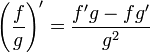…(g ≠ 0)
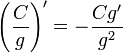(g ≠ 0)
Если функция задана параметрически:
,
то 
Основная статья: Дифференцирование сложной функции
Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
где 
— биномиальные
коэффициенты.
Следующие свойства производной служат дополнением к правилам дифференцирования:
если функция дифференцируема на
интервале 
,
то она непрерывна на интервале
.
Обратное, вообще говоря, неверно
(например, функция 
на 
);
если функция имеет локальный максимум/минимум при
значении аргумента, равном 
,
то 
(это
так называемая лемма
Ферма);
производная данной функции единственна, но у разных функций могут быть одинаковые производные.
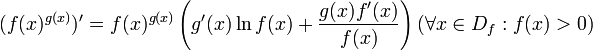
3.Основныеформулыдифференцирования.
Функция |
Производная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4, Производная неявной функции, функций заданной параметрически и степенно-
показательной функции.
Дифференцирование неявной функции
Пусть переменные х и у связаны уравнением
F (x, y) = 0. (5.12)
Если функция y = f (x) определенная на некотором интервале (a, b) такова, что обращает уравнение (5.12) в тождество при подстановке в него вместо у, т.е.
F (x, f (x)) = 0,
то y = f (x) есть неявная функция, определяемая уравнением
Производная степенно-показательной функции
Будем называть функцию
вида 
степенно-показательной.
Производная от этой функции в общем
виде имеет вид
,
т.е. производная степенно-показательной функции равна сумме производных этой функции как от степенной, а затем как от показательной.
Однако для нахождения производных степенно-показательной функции можно применить прием логарифмического дифференцирования, который позволяет легко и быстро найти производную.
1, Понятие производной, ее геометрический и физический смысл. Дифференцируемость
функции.
Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называетсядифференци́рованием.
Производная f'(x0) функции f в точке x0, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x0 тогда и только тогда, когда её производная в этой точке существует и конечна:
Геометрический и физический смысл производной
Тангенс угла наклона касательной прямой
Если функция 
имеет
конечную производншую в точкеx0, то
в окрестности U(x0) её можно
приблизить линейной
функцией
fl(x) = f(x0) + f'(x0)(x − x0).
Функция fl называется касательной к f в точке x0. Число f'(x0) является угловым коэффициентом или тангенсом угла наклона касательной прямой.
Скорость изменения функции Править
Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0)выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.
Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).