3

b

a

b

a

b

a

. Теорема 2. (Ньютона – Лейбница). Если F(x) – первообр для f(x), x[a;b], то ∫ f(x)dx = F(b) - F(a),∫ f(x)dx = F(x) │ = F(b) - F(a) Док-во.

x

a

F(x) – некот. первообр для f(x) Ф(х) = ∫ f(t)dt также первообразная. Ф'(x) = f(x), но две любые первообре отличаются на постоянные согласные т.е. ∫ f(t)dt = F(x) + C₁ пусть х=а, тогда С₁ = F(a) Cлед-но ∫ f(x)dx = F(x) - F(a) пусть x=b, тогда ∫ f(t)dt = F(b) - F(a) чтд

4. Замена переменной или способ подстановки,

Пусть мы не можем сразу найти первообр-ю для подыинт. выр-я. Сделаем замену перем. х=t по ф-ле х=(t), где (t) – непрер. и дифф. ф-я на отрезке [;] причем ()=a, (β)=b . Тогда имеет место след. рав-во:

b

a

b

a

∫ f(x)dx = ∫ f[φ(t)] * φ'(t) dt, здесь φ'(t) dt = dx Док-во. Пусть F(x) – первообр. для ф-и f(x). Тогда можно записать:

∫ f(x)dx = F(x) + C ∫ f[φ(t)] * φ'(t) dt = F[φ(t)] + C

b

a

b

a

β

α

β

α

а также

∫ f(x)dx =F(x) │= F(b)-F(a), ∫ f[φ(t)]*φ'(t)dt =F[φ(t)] │= F[(β)] - F[()]=F(b) - F(a)

Пр. часть 2-х посл. рав-в равны, значит, равны и левые. чтд

Интегрирование по частям. Рассмотрим рав-во. (u*v)' = u'v + v'u , где v,u - непрерывные ф-ции. Проинтегрируем по х от a до b:

b

a

b

a

b

a

b

a

∫ (u*v)dx = ∫ u'v dx + ∫ uv' dx

b

a

b

a

т.к. ∫ (u*v)'dx = uv + C , то ∫ (u*v)'dx = uv │ , то получим

b

a

b

a

b

a

∫ u dv = uv│ - ∫ v du , здесь du = u' dx

6.Несобств интегралы. Пусть функция f(x) определена и непрерывна на интервале [a, ). Тогда она непрерывна на любом отрезке [a, b].

Опр: Если сущ конечный предел , то он л назыв несобств интегралом от функции f(x) на интервале [a, ). Обозначение:

Если этот предел существует и конечен, то несобствй интеграл сходится.

Если предел не существует или бесконечен- несобств интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

;

Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Тео: Если для всех х (x  a) выполняется условие и интеграл сходится, то тоже сходится и  . Теор: Если для всех х (x  a) выполняется усл и интеграл расходится, то тоже расходится. Теор: Если сходится, то сходится и интеграл .В этом случае инт назыв абс сх-ся.

13. ЧАСТН ПРОИЗВОДНЫЕ 2-ГО ПОР Ф-Й НЕСК-Х ПЕР-Х.Частные производные наз-ют частными производными 1-го пор-ка. Их можно рассматривать как ф-ции от (х;у)€D. Эти ф-ции м/иметь частные производные, кот-е наз-ся частными производными 2-го пор-ка. Они определяются и обозначаются след. образом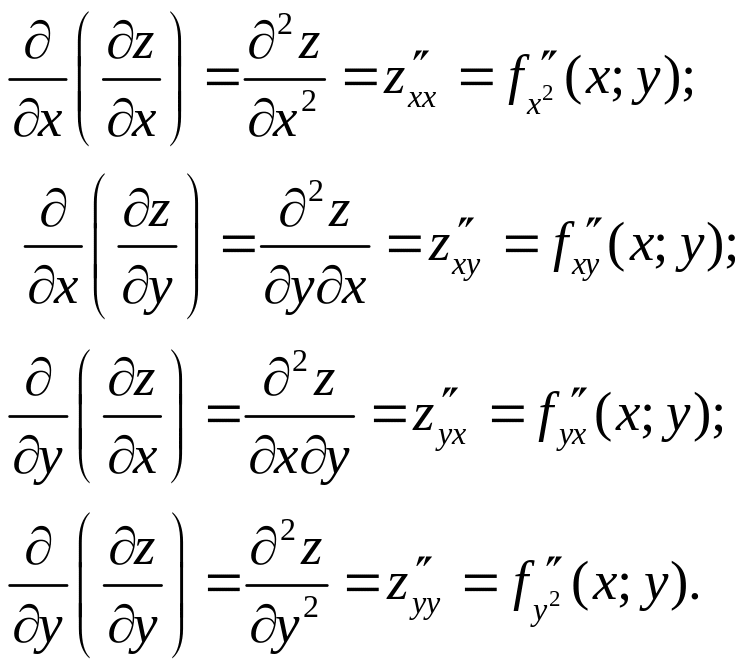

7. Понятие функции нескольких переменных.

При рассм ф-й неск-х пер-х ограничимся подробным описанием функций 2 пер-х, т.к. все получ результаты будут справедливы для функций произв числа пер-х.

Опред: Если каждой паре независимых др-от-др чисел (х, у) из некот множества по к-л правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных. z = f(x, y)

Опред: Если паре чисел (х, у) соотв одно значение z, то функция называется однозначной, а если более одного, то – многозначной.

Опред: Обл-ю опр-я функции z называется сов=сть пар (х, у), при кот= функция z существует.

9. Сложн ф-я неск-х переем и ее частн произв-ные

Если u = f(x₁,x₂,x₃….x_n) , то в случае, когда  x₁,x₂,x₃….x_n зависят  только от одной переменной t, производная по t сложной ф-ции вычисляется по формуле

а если f зависит от одной переменной х, то формула принимает вид: те совп с формулой для одномерного случая. ПРОИЗВОДНАЯ СЛОЖНОЙ Ф-ИИ НЕСК-Х ПЕР-Х. Пусть z=f(x,y) – ф 2х пер-х х и у, кажд из кот явл функцией независимой переменной t: x=x(t), y=y(t).В этом случае функция z=f[x(t);y(t)] явл сложной функцией одной независимой переменной t; переменные х и у – промежуточные переменные. Теор. Если z=f(x,y) – дифф-мая в т.М(х;у)€D функция и х=х(t) и y=y(t) – дифф-мые функции независ переменной t, то производная сложной функции z(t)= f[x(t);y(t)] вычисляется по формуле .

16. ПРИЛОЖЕНИЯ ДВОЙНОГО ИНТЕГРАЛА. Объём тела. Исходя из геоме смысла 2го инт объём цил тела нах-ся по формуле (1) где z=f(x,y) – ур пов-ти, ограничивающей тело сверху. Площадь плоской фигуры. Если положить в формуле (1) f(x,y) = 1 (частный случай), то цил тело «превратится» в прямой цилиндр с высотой H = 1. Объём такого цилиндра численно будет равен S осн-я D. Получаем формулу для вычисления площади S области D: (2). Масса плоской фигуры. Исходя из своего физического смысла двойной интеграл от ф-ции ν(x;y) численно равен массе пластинки, если подынтегральную ф-цию ν(x,y) считать плотностью этой пластинки в т. (x;y): Статич моменты и координаты центра тяжести плоской фигуры. Статические моменты фигуры D относительно осей Ox и Oy м.б. вычислены по формулам а координаты центра масс фигуры – по формулам Моменты инерции плоской фигуры. Моменты инерции плоской фигуры относительно осей Ox и Oy м.б. вычислены по формулам: Момент инерции фигуры относительно начала координат – по формуле