
- •1.Частн.Прирощ., произв., диф., их геом.Смысл.
- •2. Полный диф.Ф-ции нескольких переменных. Инвариантность ф-ции полн.Диф.
- •3. Необход. И дост. Условие диф. Ф-ции
- •6. Экстремум ф-ции нескол. Переем. Необх. И дост. Усл.
- •8. Первообр. Ф-ции и неопред. Инт.
- •12. Инт. Рациональных дробей
- •14. Инт. Тригонометрических выражений
- •15. Инт. Некот иррациональных выражений
- •16. Определенный инт. Геометр.Смысл
- •4. Произв.Сложных и неявнозад.Ф-ций
- •5. Кас.Пл. И норм. К поверхн. Скал.Поле. Градиент
- •7. Условный экстр. Метод множит. Лагранжа
- •11. Замена переменной в неопред. Инт.
- •13. Инт. Простейших рациональных ф-ций
- •17. Основные св-ва опред. Инт.
- •18. Формула Ньютана-Лейбница
- •19. Опред.Инт. С переменным верхним пределом
13. Инт. Простейших рациональных ф-ций
Будем
считать, что дробь
![]() правильная. Простейшей дробью наз
прав. Рац. дробь одного из следующих 4
типов:
правильная. Простейшей дробью наз
прав. Рац. дробь одного из следующих 4
типов:
![]()
![]()
![]()
![]() Простейшие дроби 1 и 2 типов инт.
непосредственно
Простейшие дроби 1 и 2 типов инт.
непосредственно
![]() Инт. от прост.
дроби 3 типа приводится к табл.инт.
путем выделения в числителе диф.
знаменателя и приведения знаменателя
к сумме квадратов.
Инт. от прост.
дроби 3 типа приводится к табл.инт.
путем выделения в числителе диф.
знаменателя и приведения знаменателя
к сумме квадратов.
![]()
 Для
инт. прост. дроби 4 типа преобразуем
трехчлен
Для
инт. прост. дроби 4 типа преобразуем
трехчлен![]() .Замена
.Замена![]() Тогда
Тогда
– диаметр разбиения.
Если при этом величина
 определенному приделу S,
кот не зависит от выбора т
определенному приделу S,
кот не зависит от выбора т
 на
част.отр. и не зависит от способов
разбиения (1), то S
наз площадью данной фигуры
на
част.отр. и не зависит от способов
разбиения (1), то S
наз площадью данной фигуры
 (3) Рассмотренная
задача приводит нас к опреции инт. Ф-ции
на определ.отр. результат наз. определенным
инт. от ф-ции на отр.
(3) Рассмотренная
задача приводит нас к опреции инт. Ф-ции
на определ.отр. результат наз. определенным
инт. от ф-ции на отр.
 (4) – опред.
инт. ГЕометр. Смысл:
(4) – опред.
инт. ГЕометр. Смысл:
 - площади криволинейной трапеции,
ограниченной y=f(x),Ox,x=a,x=b.
- площади криволинейной трапеции,
ограниченной y=f(x),Ox,x=a,x=b.
17. Основные св-ва опред. Инт.
1) Если нижний и вехний пределы равно, то инт.=0
2)
Если f(x)=1,
То

3) При перестановке пределов инт. меняет знак
4) Постоянный множитель можно выносить за знак инт.
5) Опр.инт. от алгеабр.суммы конечного чила интегрир. На отр [a,b] ф-ции = алгеабр. Сумме опред. инт. от слогаемых
6)
Если f(x)>0,
то и

7)
(монотонность опред.инт.) Если
 ,
то и
,
то и

8)
(об оценке опред.инт.) Если m
и M
– соот. наименш. и наибол. значения
ф-ции, то выполн. равентво

9)
(т-ма о среднем) Опред.инт. от непрерывн.
ф-ции на отр. равен произведению длины
этого отр. на значение подынтегр. ф-ции
в некот. промежут. т С:

10)
(аддитивность опред.инт.) Если сущ.
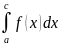 и
и
 ,
то сущ. и
,
то сущ. и
 ,
причем
,
причем


18. Формула Ньютана-Лейбница
Опред.инт.
равен приращению первообразной к
подынтегр. Ф-ции, когда независ.
переменнеая изменяется от нижнего до
верхнего предела.
 .
.
Это
и есть ф-ла Ньютана-Лейбница, она дает
правило вычисления опред.инт.: значение
опред.инт. на отр.
 от неперерывной ф-ции равно разности
значений любой ее первообразной,
вычисленной при
от неперерывной ф-ции равно разности
значений любой ее первообразной,
вычисленной при
 и
и
 Это ф-ла может принять вид
Это ф-ла может принять вид
![]() Итак,
опред.инт. равен прирощению неопредел.
Этот результат – т-ма Ньютана-Лейбница.
Итак,
опред.инт. равен прирощению неопредел.
Этот результат – т-ма Ньютана-Лейбница.
19. Опред.Инт. С переменным верхним пределом
Пусть
в
 предел а
зафиксирован
предел а
зафиксирован
