8. Первообр. Ф-ции и неопред. Инт.

Ф-ция F(x), x∈ X⊂ ,R наз первообразной для ф-ции f(x) на множестве Х, если она диф для любого x∈ X и Если F1(x) и F (x) - две различные первообр. одной и той же ф-ции f(x) на интервале (а,b), то они отличаются друг от друга постоянным слагаемым, т.е

, где С - постоянная, ∀x∈(a,b). Совокупность всех первообр. для ф-ции f(x) наз неопределенным инт. От этой ф-ции и обозн. символом

С геометр. т зрения неопределенный инт. представляет

собой однопараметрическое семейство кривых y= F(х) +C (С – параметр), обладающих следующим св-вом: все касс. к кривым в точках с абсциссой х = х0 параллельны между собой.

12. Инт. Рациональных дробей

Для того чтобы проинтегр. рац. дробь, необходимо

выполнить следующие действия: 1) если рассматриваемая рац. дробь P _к(x)/Q_м(x)- неправильная, представить её в виде суммы многочлена и прав. Рац.дроби: 2) если рассматр. рац. дробь - прав., представить её в виде суммы простейших рац. дробей по формуле;

3) инт. от рац. дроби представить в виде суммы инт. от

целой части и от соответствующих простейших дробей и вычислить эти инт.

14. Инт. Тригонометрических выражений

1)

2) если хотя бы 1 из m или n – полож. Целое нечетное, то (допустим, что n):подносим под dx

Если m и n – полож. Четное число, то необходимо понизить степень sin или cos путем перехода к удвоенным аргументам, т.е. использовать ф-лы:

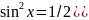
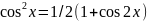
3) Замена: tg x = t, ctg x = t,

x = arctg t, dx = dt/1+t² , tg²x =1/cos²x – 1, ctg²x = 1/sin²x –1

4) С помощью универсальной подст.:

15. Инт. Некот иррациональных выражений

1) Замена , s-общий знаменатель всех х

2) . Замена

3) . Замена x=a sin(t)

. Замена x=a tg(t)

. Замена x=a/cos(t)

4) . Путем разложения полного квадрата представить в виде 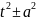и ввести замену

5) Если а) s – общий знаменатель m и n; б) s - знаменатель p; в) , s - знаменатель p.

16. Определенный инт. Геометр.Смысл

Пусть нужно найти S(aABb) ограниченной y=f(x),Ox,x=a,x=b.

Фигура наз. криволинейной трапецией. Пусть . Разобьем отр. произв. отр. На n частей точками х₀, х₁, х₂,…х_n,так чтобы х₀< х₁< х₂<…< х_n=b (1). Пусть

В каждом из частичных отр. выберем произв. т и составим сумму: (2) Сумма (2) наз. инт. Суммой для ф-ции f(x) на отр. или инт. Суммой Римана. Сумма = сумме заштрих. прямоугольников. Устремим все длины част.отр. к 0, так чтобы длина наидол. Част.отр.