Распр. Скор при лам и торб режимах.

Распр-е скоростей в ламинарном потоке. Поскольку ламинарный поток жид­кости в круглой цилиндрической трубе является осе симметричным, рассмотрим вертикальное сечение трубы. Тогда, согласно гипотезе Ньютона:

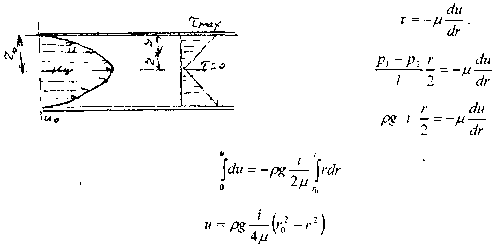
Отсюда видно, что распределение скоростей в круглой цилиндрической трубе соот­ветствует параболическому закону. Макс величина скорости будет в центре тру­бы, где = О

Ср скорость движения жидкости в ламинарном потоке. Для определения вели­чины средней скорости рассмотрим живое сечение потока жидкости в трубе. Затем прове­дём в сечении потока две концентрические окружности, отстоящие друг от друга на бес­конечно малое расстояние dr. Между этими окружностями мы, выделили малую кольцевую зону, малую часть живого сечения потока жидкости. Расход жидкости через выделенную кольцевую зону: через полное живое сечение трубы: величина средней скорости в сечении:

Распределение скоростей по сечению турбулентного потока. Наблюдения за величи­нами осреднённых скоростей в турбулентном потоке жидкости показали, что эпюра осреднённых скоростей в турбулентном потоке в значительной степени сгла­жена и практически скорости в разных точках живого сечения равны средней скорости. Сопоставив эпюры скоростей турбулентного и ламинар­ного потока можно сделать вывод о практически равномерном распределении скоро­стей в живом сечении. Работами Прандтля было установлено, что закон изменения каса­тельных напряжений по сечению потока близок к логариф-му закону. При некото­рых допущениях: течение вдоль бесконечной плоскости и равенстве касательных напря­жений во всех точках на поверхности . 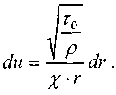После интегр: Последнее выражение преобразуется к следующему виду: 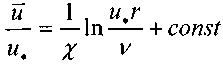Развивая теорию Прандтля, Никурадзе и Рейхардт предложили аналогичную зависи­мость для круглых труб.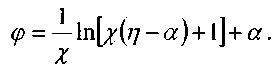

Основы гидродинамического подобия

Гидродинамическое подобие  - это подобие потоков несжимаемой жидкости, вкл-е в себя подобие геом-ое, кинем-ое и динамическое. Из геометрии известно, что геометрическое подобие  означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки жидкости, Таким образом в гидравлике геометрическое подобие означает подобие русел или трубопроводов, по которым течёт жидкость.

Кинематическое подобие это подобие линий тока и пропорциональность сходственных скоростей. Это значит, что для кинематического подобия потоков требуется соблюдение геометрического подобия.

Динамическое подобие заключается в  пропорциональности сил, действующих на сходственные элементы кинематически и геометрически подобных потоков, и равенство углов, характеризующих направление действия этих сил. В потоках жидкостей (в нашем случае в трубопроводах, в гидромашинах и т.д.) обычно действуют разные силы – силы давления, силы вязкого трения, силы тяжести, инерционные силы. Соблюдение пропорциональности всех сил, действующих в потоке, означает полное гидродинамическое подобие.

На практике полное гидродинамическое подобие достигается редко, поэтому обычно приходится ограничиваться частичным (неполным) гидродинамическим подобием, при котором имеется пропорциональность лишь основных сил.

Записывается подобие следующим образом. Например, пропорциональность сил давления Р и сил трения Т, действующих в потоках I и II, можно записать в виде

.
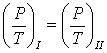