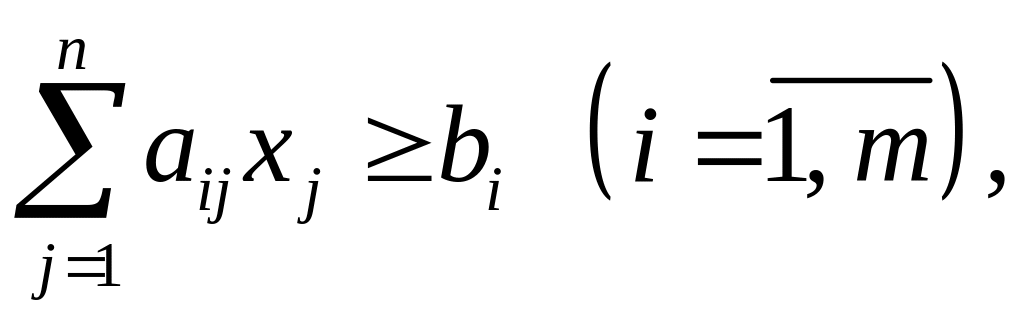Глава 1. Линейное программирование

§1. Общая постановка задачи линейного программирования

Линейное программирование – раздел прикладной математики, занимающийся методами исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции многих переменных, на независимые переменные которых наложены линейные ограничения.

Такая линейная функция называется целевой, а набор количествен­ных соотношений между переменными, выражающих определенные требования экономической задачи в виде уравнений или неравенств, называется системой ограничений. Совокупность соотношений, содержащих целевую функцию и ограничения на ее аргументы, называется математиче­ской моделью экономической задачи оптимизации. Слово «программирование» введе­но в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу (план) работы некоторого экономического субъекта.

К задачам линейного программирования приводят исследования производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Задача линейного программирования (ЗЛП) ставится следующим образом: найти экстремум (максимум или минимум) линейной целевой функции

, (1.1)

при линейных ограничениях:

(1.2)

(1.3)

где , , ( , ) – известные величины, ( ) – управляющие переменные. Формулы (1.1) – (1.3) представляют собой запись задачи линейного программирования в развернутом (координатном) виде.

Матричная запись ЗЛП имеет вид:

,

,

,

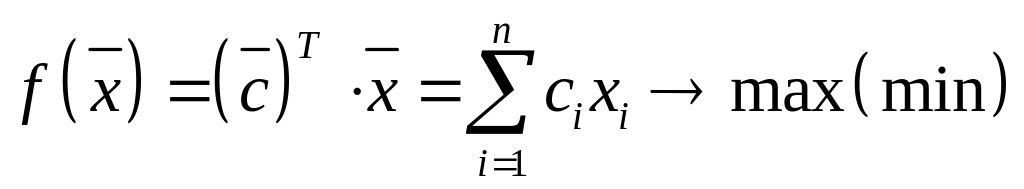где – вектор-столбец коэффициентов целевой функции, – вектор управляющих переменных, – вектор-столбец свободных членов, – матрица коэффициентов при управляющих переменных (матрица условий).

Определение 1.1. Систему (1.2) называют системой функциональных, или ресурсных ограничений задачи линейного программирования.

Определение 1.2. Неравенства (1.3) называют прямыми ограничениями задачи линейного программирования.

Определение 1.3. Вектор , удовлетворяющий системе неравенств (1.2) – (1.3), называют допустимым решением или допустимым (опорным) планом задачи линейного программирования.

Определение 1.4. Допустимое решение , доставляющее целевой функции максимум или минимум, называют оптимальным решением, или оптимальным планом задачи линейного программирования.

Неравенства (1.2) – (1.3) определяют область допустимых решений задачи линейного программирования.

Формы записи злп, их эквивалентность и способы преобразования

Задачу линейного программирования можно записать в одной из приведенных ниже форм.

Общая форма записи:

,

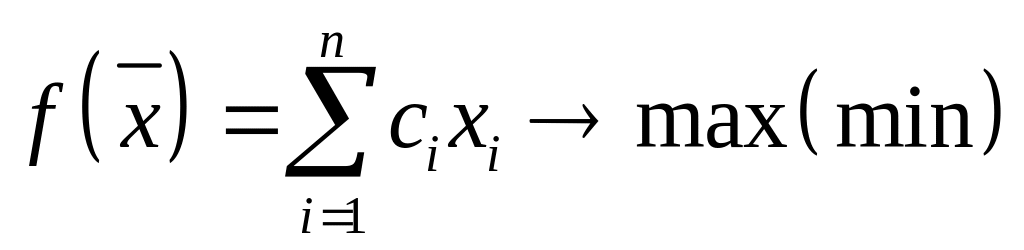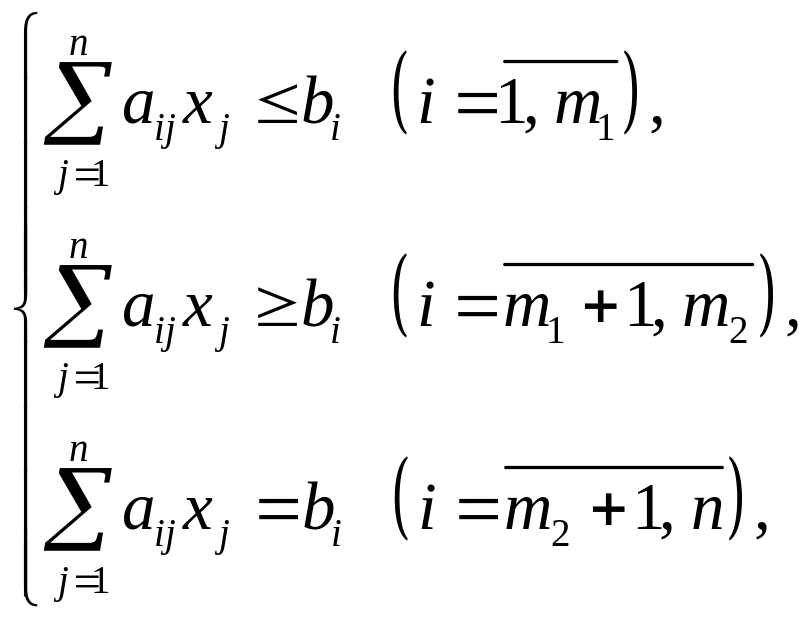
произвольного знака .

Симметрическая (стандартная) форма записи:

,

,

Каноническая форма записи:

,

.

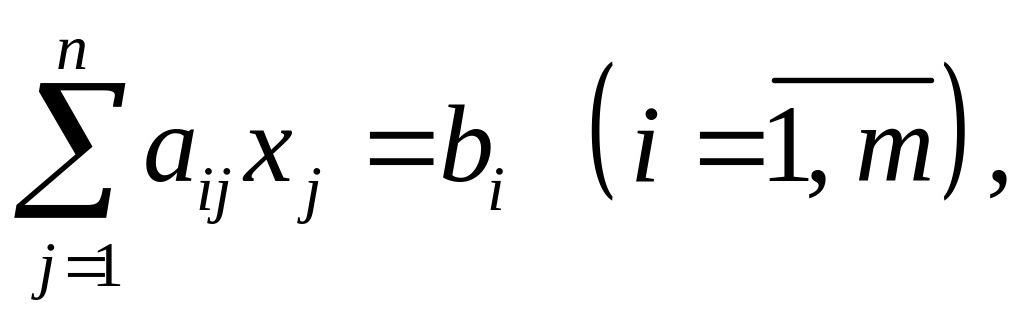
Указанные формы записи ЗЛП эквивалентны в том смысле, что в результате некоторых преобразований можно перейти от одной формы записи к другой. Если имеется способ нахождения оптимального решения ЗЛП, записанной в одной форме, то можно определить и оптимальное решение ЗЛП, записанной в другой форме.

Замечание 1.1. Задачу максимизации целевой функции можно заменить задачей минимизации:

.

Замечание 1.2. Неравенство типа можно заменить на неравенство типа путем умножения обеих частей этого неравенства на число .

Замечание 1.3. Ограничение-неравенство вида

преобразуется в ограничение-равенство путем введения так называемой балансовой неотрицательной переменной :

.

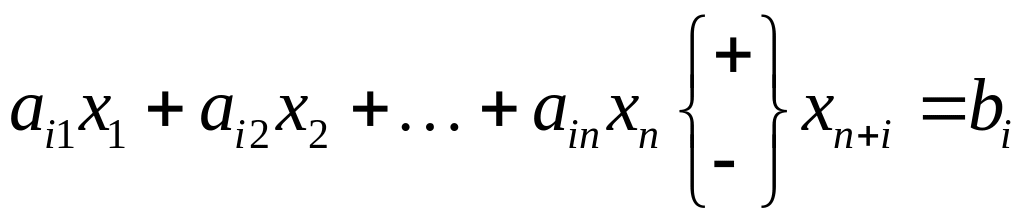Рассмотрим на примерах способы перехода от одной формы записи ЗЛП к другой форме записи.

Пример 1.1. Привести к канонической форме записи ЗЛП:

,

.

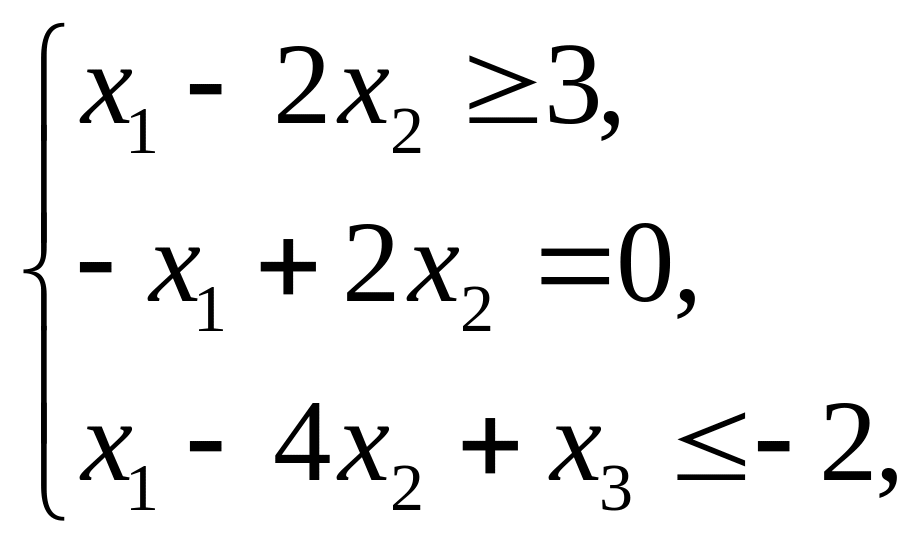
Решение. ЗЛП представлена в общей форме записи. Для сведения ее к канонической форме в первое и третье ограничения-неравенства введем балансовые переменные . Изменим также тип экстремума, введя целевую функцию . Тогда

,

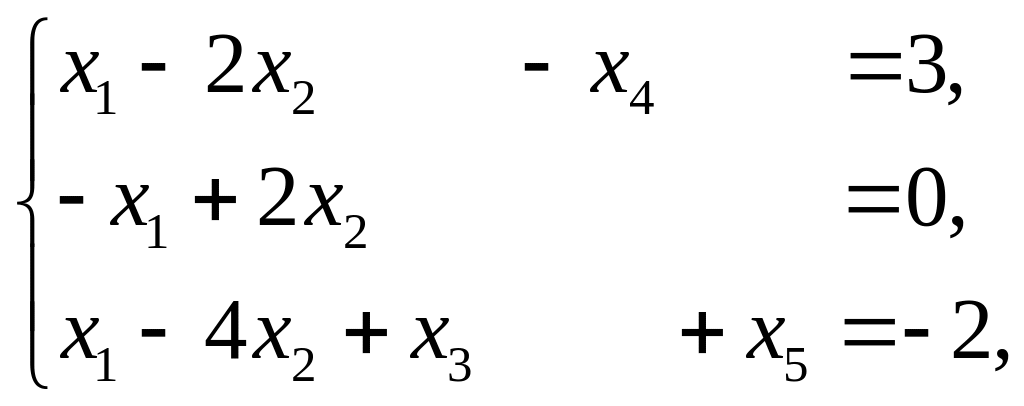
Пример 1.2. Привести к симметрической форме записи ЗЛП

,

.

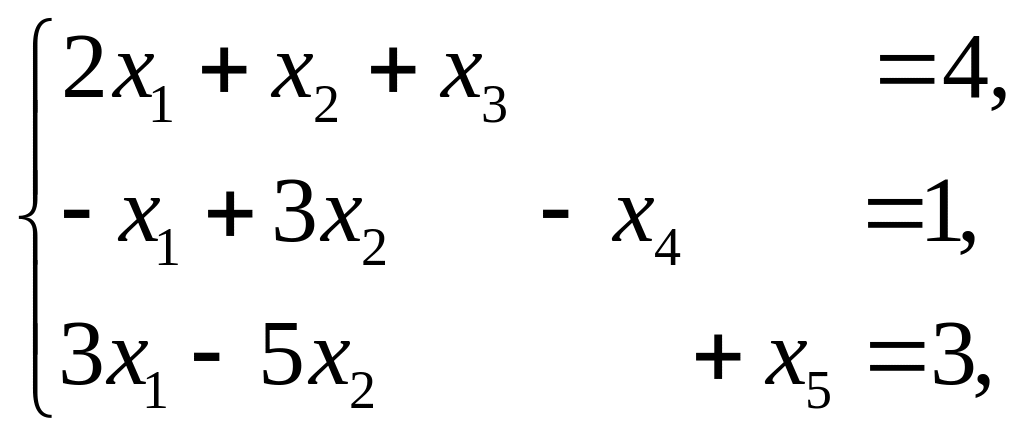
Решение. ЗЛП представлена в канонической форме записи. Для сведения ее к симметрической форме записи исключим (выразим) три переменные через остальные переменные. В данном случае удобно выразить переменные через , и учесть условие их неотрицательности:

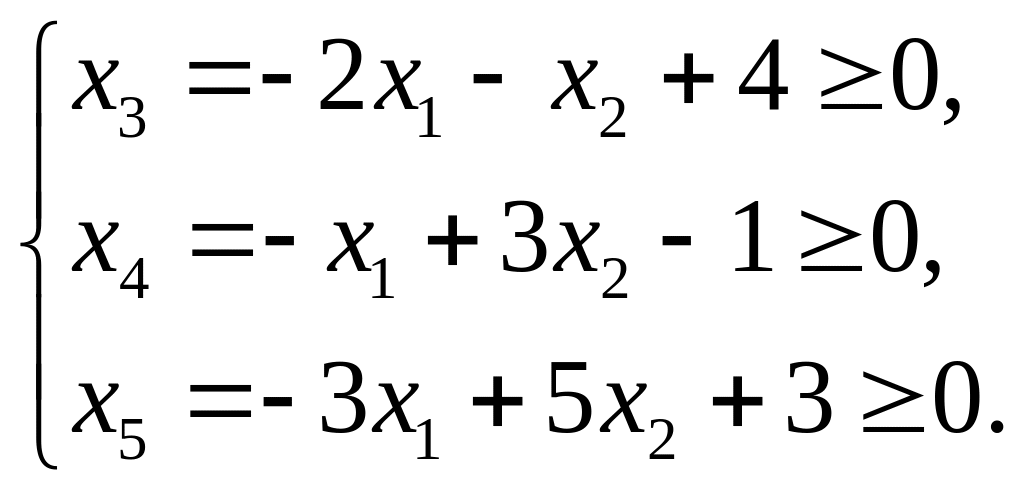
Опустив переменные , придем к эквивалентным неравенствам. Для получения целевой функции симметрической задачи необходимо вместо переменных подставить выражения из последней системы в исходную целевую функцию

.

В результате получаем симметрическую ЗЛП

,

.
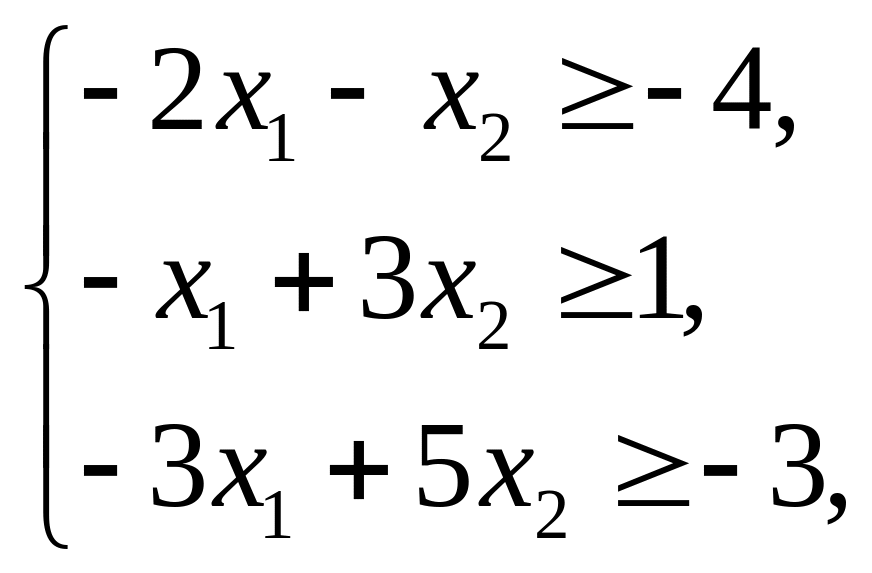
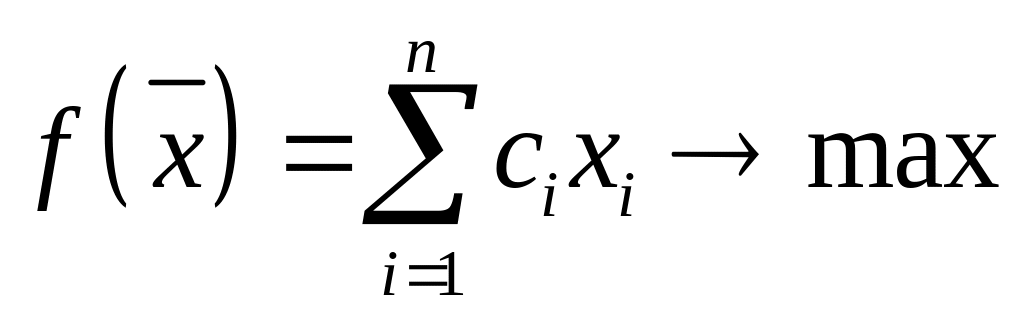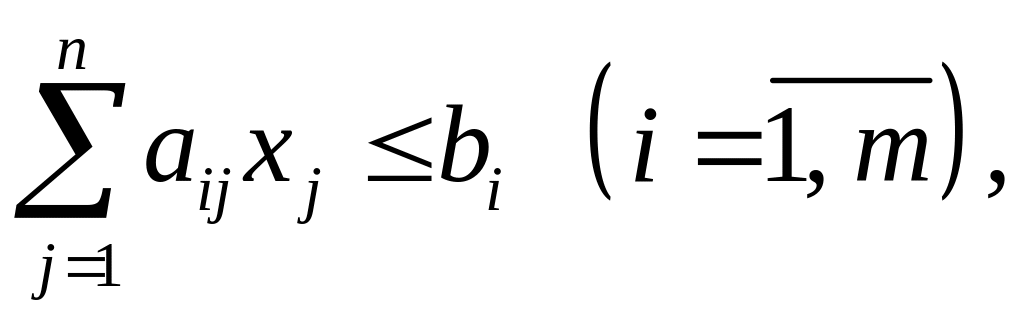
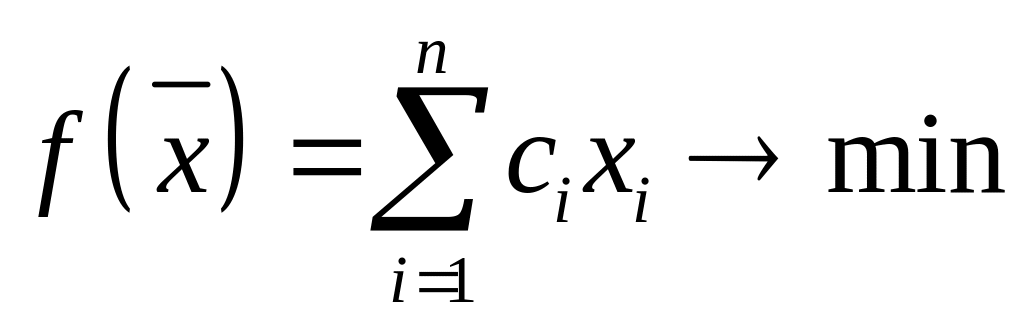