28. Вращение вокруг неподвижной оси

Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения. Положение вращающегося твердого тела определяется одним параметром - углом φ между начальным положением АМ₀О некоторой плоскости, связанной с телом и проходящей через ось, и ее положением АМО в данный момент времени Рисунок 1.

Закон вращательного движения:

Проекция вектора угловой скорости на ось и определяется зависимостью:

Угловая скорость ω рад/сек связана с числом оборотов в минуту n зависимостями:

Проекция вектора угловой скорости на ось u определяется зависимостью

Скорость и ускорение точки М вращающегося твердого тела определяются соотношениями (рис. 1):

или в скалярной форме:

Частные случаи:

1) равномерное вращение (ε=0):

2) равнопеременное вращение (ε_u=const):

29)Векторное выражение вращательной скорости и центростремительного ускорения.

В дальнейшем при рассмотрении общих случаев движения твердых тел придется иметь дело с вращениями вокруг подвижных осей, меняющих свое направление в пространстве. В этих случаях уже нельзя довольствоваться рассмотрением угловой скорости и углового ускорения как алгебраических величин, а становится необходимым связывать их с ориентацией в пространстве. Это достигается, если ввести угловые скорости и ускорения как векторы и в связи с этим для векторов линейных скоростей и ускорений установить векторные формулы, представляющие эти величины как по величине, так и по на-

правлению. Введем в рассмотрение вектор угловой скорости, который будем обозначать через w.

Величиной вектора угловой скорости w является

Направление вектора угловой скорости естественно связать с осью вращения твердого тела. Необходимо указать, в какую сторону по оси вращения откладывать вектор w.

Выбрав положительное направление оси вращения, условимся относительно направления положительного отсчета углов поворота тела, связывая его с направлением поворота оси Ох к оси Оу на π/2, если смотреть с положительной стороны оси Оz. Такое условие позволяет сохранить одинаковое определение положительного поворота как в правой, так и в левой системе координат, хотя положительный поворот в правой системе происходит в сторону, противоположную положительному повороту в левой системе; при этом

все аналитические формулы (т. е. формулы, заключающие проекции на оси координат) сохраняют одинаковый вид как в правой, так и в левой системе координат.

Условимся направлять вектор угловой скорости w по оси вращения так, чтобы наблюдатель, смотрящий с конца вектора w, видел вращение тела в положительном

направлении, т. е. против часовой стрелки при правой системе координат (рис. 139)

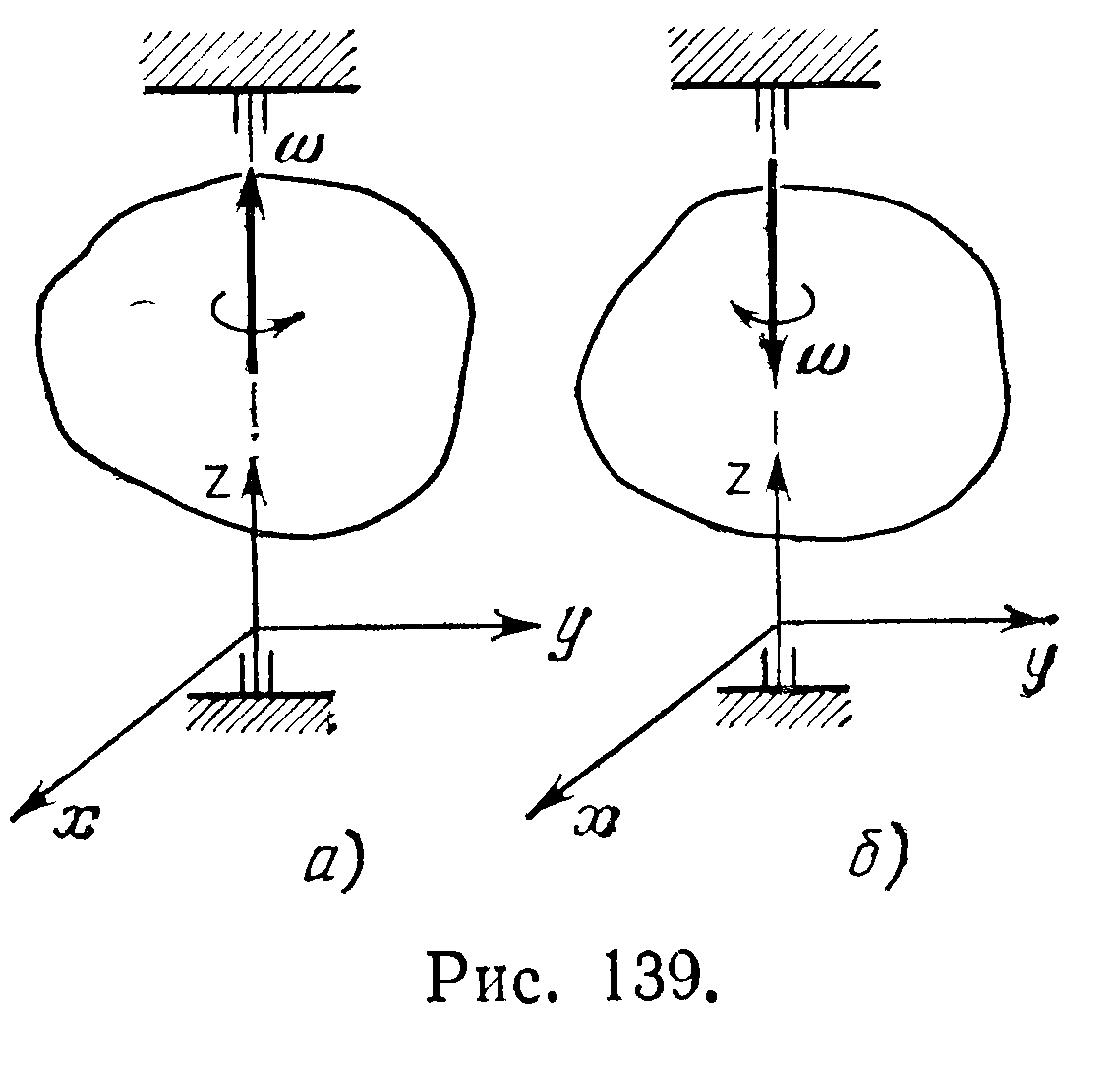
Так, например, при правой системе координат вектор угловой скорости вращения Земли направлен к Северному полюсу. Направление вектора угловой скорости совпадает с направлением осевого движения правого винта при ввинчивании его в неподвижную гайку.

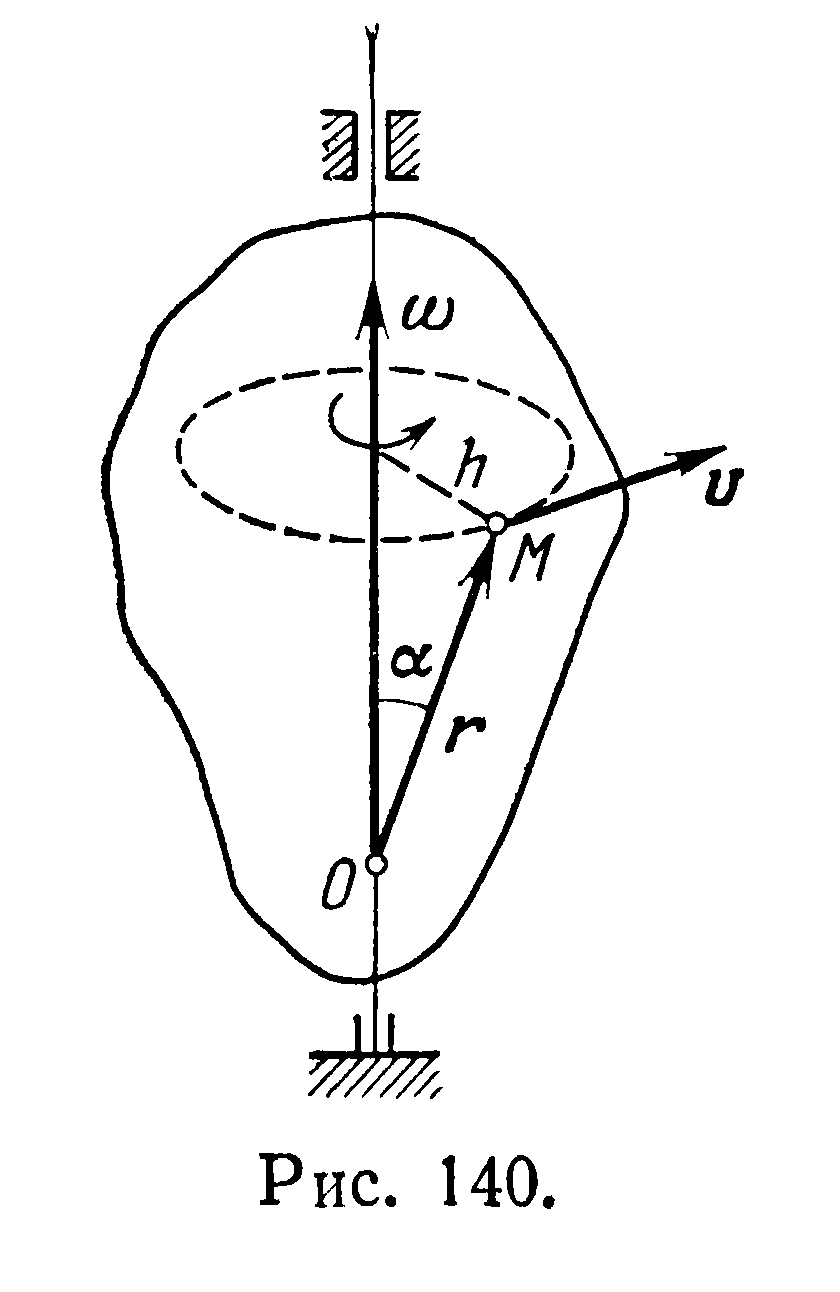
Откладывая вектор w по оси вращения, можно определить вектор линейной скорости v любой точки М как векторное произведение вектора угловой скорости на вектор-радиус этой точки относительно любой точки оси вращения (рис. 140):

В самом деле, величина векторного произведения (20) равна

К равенству (20) можно прийти также, рассматривая величину вектора скорости v по (21) как величину момента вектора угловой скорости w относительно центра М. По определению момента будем иметь

где r' = —r есть вектор-радиус точки О относительно М. Отсюда по известному свойству векторного произведения следует

Формула (20) является основной формулой кинематики твердого тела; как увидим далее, она сохраняет свой вид не только в случае вращения вокруг неподвижной оси, но и в случае вращения тела вокруг неподвижной точки.

Проектируя обе части (20) на координатные оси, найдем проекции скорости. Если принять ось вращения за ось Оz, то проекции вектора w будут равны

По известным формулам проекций векторного произведения получим

где х и у (z не входит в эти формулы) —координаты точки М.

Если координатные оси ориентированы произвольно, то, обозначая через w_x,w_y,w_z проекции на них вектора w, получим формулы Эйлера:

Формулам Эйлера (23) можно придать удобный для запоминания вид определителя:

Выведем теперь векторную формулу ускорения. Для этого возьмем векторную производную по времени от обеих частей равенства (20); будем иметь

Производную по времени от вектора угловой скорости w назовем вектором углового ускорения. Так как в рассматриваемом случае о является вектором постоянного направления (ось вращения неподвижна), то, согласно сказанному в начале, величина углового ускорения будет равна абсолютному значению производной от величины угловой скорости, а направление его или совпадает, или противоположно w сообразно тому, возрастает или убывает с течением времени величина угловой скорости . Называя вектор углового ускорения в согласии с ранее введенным обозначением ε и замечая еще, что по определению скорости dr/dt = v, приведем (24) к виду

Первое слагаемое, ε• r, представляет собой вращательную составляющую ускорения. Действительно, оно равно по величине εr sin (ε, r) = εh, а по направлению совпадает со скоростью v = ω• r, если векторы ω и ε сонаправлены, и противоположно скорости, если ω и ε разнонаправлены; первое будет иметь место в ускоренном, а второе — в замедленном вращение.

Второе слагаемое в формуле (25) представляет собой осестремительное ускорение. Его величина равна ωvsin(ω,v) = ω²h; так как векторы ω и v взаимно перпендикулярны, а v=ωh. Направление векторного произведения v•ω перпендикулярно к оси вращения (вектору ω) и скорости v, т. е. идет по радиусу круга, описываемого точкой, к его центру. Итак, действительно,

Формулы (20) и (26) представляют собой векторные обобщения формул (15) и (17).