1 Устойчивость сжатых стержней (основные положения теории)

1.1 Понятие об устойчивости

Во многих случаях центрально сжатый стержень разрушается не только из-за нарушения прочности или жесткости, но и потому, что он не сохраняет своего исходного равновесного состояния, то есть теряет устойчивость.

Нагрузку, превышение которой вызывает потерю устойчивости стержня, называют критической силой .

На рисунке 1.1,а показано устойчивое равновесие центрально сжатого стержня, когда сжимающая сила меньше критической. При нагрузке, превышающей критическую (рисунок 1.1,б), прямолинейная форма стержня перестает быть устойчивой, он изогнется. Критическая нагрузка – это опасная нагрузка, которую допускать в реальных стержнях нельзя. В практике известны случаи, когда из-за потери устойчивости отдельных стержней разрушались мосты, металлические каркасы зданий, башен и т.п. 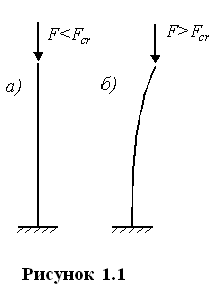Особая опасность потери устойчивости заключается в том, что обычно она наступает внезапно. Почти до наступления критической силы деформации могут быть незаметны. Имеется ряд факторов, способствующих значительному снижению сопротивления устойчивости сжатых стержней: эксцентриситет нагрузки, начальная кривизна стержня, местные напряжения, повреждения и неоднородность материала и др. В целях безопасности допускаемая нагрузка должна быть меньше критической:

, (1.1)

где - коэффициент запаса устойчивости (индекс s от stability – устойчивость).

Коэффициент запаса устойчивости обычно принимается несколько большим коэффициента запаса прочности, так как учитываются дополнительные неблагоприятные обстоятельства: начальная кривизна стержня, возможный эксцентриситет действия нагрузки и др.

Критическая сила вызывает в сжатом стержне критическое напряжение:

. (1.2)

Поэтому при расчете стержней, исходя из условия прочности, следует добавить еще и условие устойчивости:

, (1.3)

где - допускаемое напряжение на устойчивость.

Таким образом, чтобы рассчитать стержень на устойчивость, необходимо уметь определять величину критической силы.

1.2 Формула Эйлера для определения критической силы сжатого стержня

Впервые задачу об определении критической силы поставил и решил великий математик и механик, академик Петербургской Академии наук Л.Эйлер в 1744г. Рассмотрим шарнирно опертый, центрально сжатый стержень постоянного сечения (рисунок 1.2). Под действием сжимающей силы, равной критической силе или несколько больше ее, стержень изогнется. Совместим начало координат с центром нижнего сечения, направив ось y в сторону прогиба стержня, а ось z – по оси стержня.

Если моменты инерции относительно двух главных центральных осей поперечного сечения (J_x, J_y) не равны между собой, то изгиб стержня произойдет в плоскости наименьшей жесткости, то есть поперечные сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение (J_min). В этом легко убедиться, сжимая гибкую линейку.

Д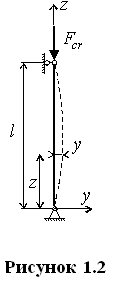 еформацию изгиба стержня предположим весьма малой, поэтому для решения задачи можно воспользоваться дифференциальным уравнением изогнутой балки:

. (1.4)

В произвольном сечении на расстоянии z от нижнего конца прогиб стержня равен y, а изгибающий момент . Тогда, решая уравнение (1.4) относительно , можно получить формулу для определения критической силы:

(1.5)

Это и есть формула Эйлера. Из формулы видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.