Дифференциальное исчисление функции нескольких переменных.

Если каждому набору х1, х2, …х_n, из некоторого множества Х соответствует одно вполне определенное значение переменной z, то говорят, что задана функция нескольких переменных z = f (x₁, x₂,…x_n), где х₁, х₂,…х_n – независимые переменные (аргументы), а z - зависимая переменная (функция).

Пусть каждой упорядоченной паре чисел (x,y) из некоторого множества D соответствует определенное число z из множества R, тогда z = f (x , y), называется функцией двух независимых переменных x и y.

Множество точек (x, y), при которых z=f(x , y) имеет смысл, называется областью определения функции (обозначается D), а множество значений, принимаемых z в области определения, называется областью изменения функции (обозначается Е).

Графиком функции двух переменных называется поверхность, состоящую из точек М(x; y; z) трехмерного пространства, координаты которых удовлетворяют уравнению z=f(x , y).

Предел и непрерывность функции двух переменных.

Число А называется пределом функции z=f(x, y) в точке М₀(х₀,у₀) (при х→х₀, у→у₀), если

Такой предел иногда называют двойным пределом и обозначается .

При вычислении двойных пределов используют известные теоремы о пределах.

Теорема (о пределах). Пусть функции f(x,y) и g(x,y) – две функции, определенные в некоторой проколотой окрестности точки М₀(х₀,у₀) и и . Тогда

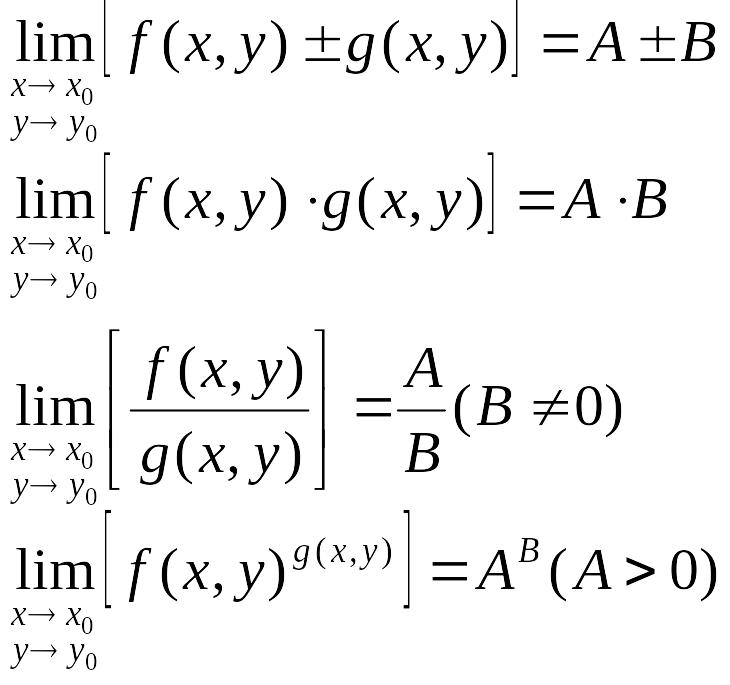
Функция z=f(x,y) называется непрерывной в точке М₀(х₀,у₀), если она:

1. определена в этой точке и некоторой ее окрестности,

2. имеет конечный предел при х®х₀ и у ® у₀ ,

3. этот предел равен значению функции в этой точке

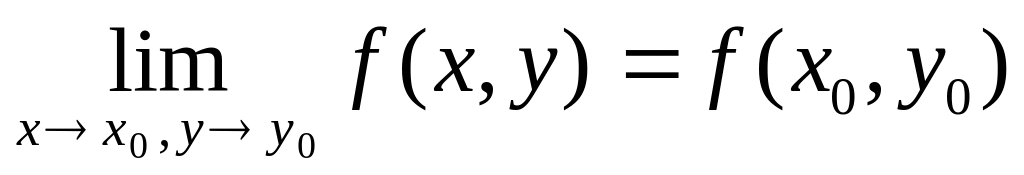
Функция z=f(x,y) называется непрерывной в точке М₀(х₀,у₀), если выполняется равенство .

Если функция f(x,y) не определена в точке М₀(х₀,у₀) или , то точка М₀(х₀,у₀) называется точкой разрыва этой функции.

Точки разрыва могут образовывать целые линии разрыва. Например, функция z=2/(y-x) имеет линию разрыва у=х.

Теорема (о переходе к пределу). Если функция f(x,y) непрерывна в точке М₀(х₀,у₀), то .

Теорема (о сохранении знака). Если функция f(x,y) непрерывна в точке М₀(х₀,у₀) и f(x,y) >0 (или f(x,y) <0), то найдется такая d – окрестность точки М₀(х₀,у₀), в которой f(x,y) >0 (или f(x,y) <0).

Теорема (о непрерывных функциях). Пусть функции f(x,y) и g(x,y) - две функции, определенные в некоторой окрестности точки М₀(х₀,у₀) и непрерывные в этой точке. Тогда в этой точке непрерывны также функции .

Частные производные и дифференциалы функции двух переменных.

Частным приращением функции z=f(x,y) по переменной x будем называть разность: ∆_xz = f(x+∆x, y) – f(x, y), где переменная x получила приращение Δx, а y осталась постоянной.

Частным приращением функции z=f(x,y) по переменной у будем называть разность ∆_yz = f(x, y+∆ y) – f(x, y), где переменная у получила приращение Δy, а х осталась постоянной.

Полным приращением функции z=f(x,y) называется разность: ∆z = f(x+∆x, y+∆ y) – f(x, y).

В общем случае полное приращение не равно сумме частных приращений: ∆z ≠ ∆_xz +∆_yz.

Если существуют конечные пределы и , то их называют частными производными функции z=f(x,y) по х и по у соответственно. При этом записывают:

Частная производная находится по правилам дифференцирования одной переменной, причем остальные переменные рассматриваются в этом случае как постоянные, т.е. если находят z´_x то считается постоянной переменная у; если находят z´_y - то переменная х.

Дифференциал функции двух переменных.

Полным дифференциалом или просто дифференциалом dz функции z=f(x,y) называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, то есть dz=z´_x∆x + z´_y ∆ y.

Учитывая, что дифференциал от независимой переменной равен ее приращению (∆x = dx, ∆ y = dy), то можно записать dz = z´_xdx + z´_y dy.

Функция z=f(x,y) называется дифференцируемой в точке М(х,у), если ее полное приращение в этой точке можно представить в виде ∆z = dz + α∆x + β∆y, где α и β –бесконечно малые величины.

Дифференциал функции z=f(x,y), найденный при условии, что одна из независимых переменных изменяется, а вторая остается постоянной, называется частным дифференциалом и обозначается: d_xz = z´_xdx, d_yz = z´_y d y.

Теорема (необходимое условие дифференцируемости функции). Если функция z=f(x,y) дифференцируема в точке М(х,у), то она непрерывна в этой точке, имеет в ней частные производные z´_x и z´_y.

Следствием теоремы является формула для вычисления полного дифференциала

или .

Теорема (достаточное условие дифференцируемости функции). Если функция z=f(x,y) имеет непрерывные частные производные z´_x и z´_y в точке М(х,у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой

.

Производная сложной функции.

Пусть z=f(x,y) , при этом х и у являются функциями независимой переменной t: x = x(t), y = y(t). В этом случае функция z = f(x(t), y(t)) является сложной функцией одной независимой переменной t; переменные х и у – промежуточные переменные.

Теорема. Если z=f(x,y) – функция, дифференцируемая в точке М(x,y)Π D и x = x(t), y = y(t)- дифференцируемые функции независимой переменной t, то производная сложной функции z = f(x(t), y(t)) вычисляется по формуле

В частном случае, если z=f(x,y), где y = y(x), т.е. z = f(x, y(x)) сложная функция одной независимой переменной х, то

.

Свойство инвариантности: полный дифференциал функции z=f(x,y) сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.

В случае, если z=f(x,y), где x = x(u, v) и y = y(u, v), т.е. z = f(x(u,v), y(u,v)) = F(u,v), где u,v - независимые переменные. Тогда

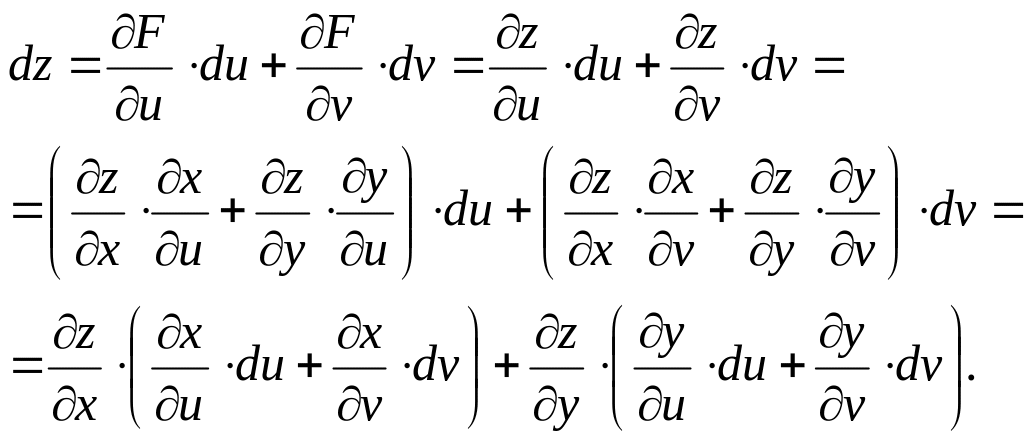
Частные производные и дифференциалы высших порядков функции двух переменных.

Частными производными второго порядка функции z=f(x,y) называют частные производные, взятые от частных производных первого порядка:

Частная производная второго порядка, взятая по различным переменным z˝_xy , называется смешанной производной второго порядка.

Теорема. Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.

Дифференциалом второго порядка функции z=f(x,y) называется дифференциал от дифференциала первого порядка этой функции: при этом записывают d²z = d(dz).

Если z=f(x,y), где х и у независимые переменные и функция f имеет непрерывные частные производные второго порядка, то d²z вычисляется по формуле:

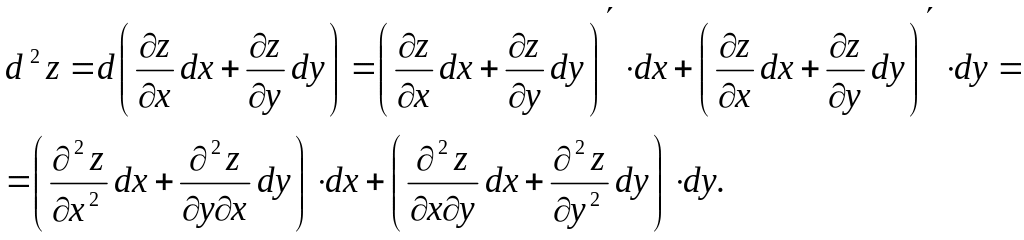
Отсюда

.

Символически это записывается

.

Аналогично получается формула для дифференциала n- порядка

.

Производная по направлению. Градиент.

Пусть функция z=f(x,y) определена в некоторой окрестности точки М₀(x,y), l – некоторое направление, задаваемое единичным вектором , где cosα, cosβ - косинусы углов, образуемых вектором с осями координат и называемыми направляющими косинусами.

При перемещении из т. М₀(x,y) в т. М₁(x,y) в данном направлении l функция z=f(x,y) получает приращение ∆_lz = f(x+∆x, y+∆y) – f(x,y), называемое приращением функции z в данном направлении l.

Производной по направлению l функции f(x,y) называется предел отношения приращения функции в этом направлении к величине перемещения ∆l при стремлении последней к нулю, т.е.

Градиентом функции z=f(x,y) называется вектор с координатами (z´_x ,z´_y)

Градиент в данной точке характеризует направление максимальной скорости изменения функции в этой точке.

Экстремум функции двух переменных. Условный экстремум функции двух переменных.

Точка М₀(х₀,y₀) называется точкой локального максимума (минимума), если ∀M(x,y) ≠ M₀(x₀, y₀) и принадлежащих достаточно малой ее окрестности, выполняется неравенство f(х₀,y₀) ³ f(х,у) (f(х₀,y₀) £ f(х,у)).

Теорема (необходимые условия существования экстремума). Если т. М₀(х₀,y₀) является точкой экстремума функции f(х,у), то или хотя бы одна из этих частных производных не определена в точке М₀(х₀,y₀).

Точки, для которых эти условия выполнены, называются стационарными или критическими.

Теорема (достаточные условия существования экстремума). Пусть т. М₀(х₀,y₀) является стационарной для функции z=f(х,y), которая имеет непрерывные частные производные до 2-ого порядка включительно в некоторой окрестности т. М₀(х₀,y₀).

Вычислим D=А·С–В², где

Тогда:

1. если D> 0, то т. М₀(х₀,y₀) является точкой экстремума, причем М₀ будет точкой максимума при А< 0 и точкой минимума при А> 0;

2. если D< 0, то в точке М₀(х₀,y₀) экстремума нет;

3. если D= 0, то о наличии экстремума ничего сказать нельзя, необходимы дополнительные исследования в точке М₀(х₀,y₀).

Условный экстремум функции двух переменных.

Это задача нахождения экстремума функции на множестве, удовлетворяющем некоторому условию.

Пусть функция f(х,у) – это функция, у которой аргументы удовлетворяют условию g(х,у)=С, называемому уравнением связи.

Точка М₀(х₀,y₀) называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что ∀M(x,y) из этой окрестности, удовлетворяющих условию g(х,у)=С, выполняется неравенство

f(х₀,y₀) ³ f(х,у) (f(х₀,y₀) £ f(х,у)).

Нахождение экстремума функции, при условии, что переменные удовлетворяют уравнениям связи, называется задачей на условный экстремум:

z=f(х,у) →max( min)

g(х,у) =b

Предполагается, что вид функций g(х,у) известен, а b– постоянная величина.

Алгоритм решения задачи на условный экстремум методом множителей Лагранжа

1. Составляют функцию Лагранжа: L(x,у,λ )= f(х,у)+ λ(b–g(х,у))

2. Находят частные производные функции Лагранжа по переменным x ,у, λ и записывают стационарную систему:

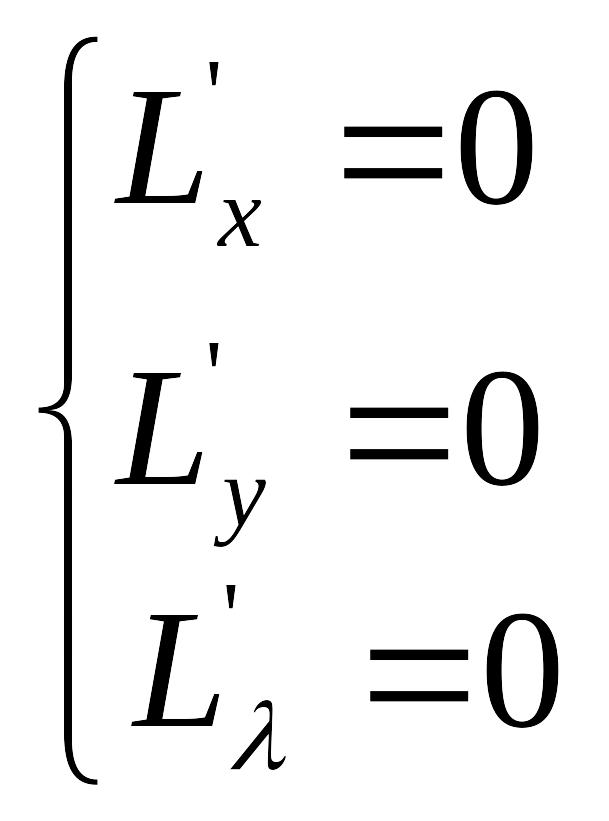
3. Находят критические точки функции Лагранжа, решая систему.

4. Находят частные производные второго порядка и вычисляют значения d²L в исследуемых критических точках M(x,у,λ).

5. Анализируют знак d²L(M(x,у,λ))

Если d²L<0, то в т. M(x,у,λ) f(х,у) имеет условный максимум.

Если d²L>0, то в т. M(x,у,λ) f(х,у) имеет условный минимум.