15. Критерии оптимальности и единственности плана транспортной задачи.

Критерий оптимальности транспортной задачи

            План перевозок

                                   

является оптимальным планом тогда и только тогда, когда найдется система платежей

                                   

для которой выполняются условия :

            

16. Общее, классическое и статистическое определение вероятности.

 Вероятность P(A) события А определяется по формуле

,

где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания.

Классическое определение вероятности события. Случаи равновероятных исходов

Классическое определение вероятности связано с определением благоприятствующего исхода. Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события. Вероятность события  равна отношению числа равновозможных благоприятствующих элементарных исходов к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания

Это определение предложил еще сам Лаплас, поэтому оно также называется лапласовским

определением вероятности. Область его применения ограничена, а именно,

предполагается, что А— событие в конечном множестве равновероятных исходов.

Тогда вероятность события обозначается и определяется так:

Р(А)= А/

Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. В примере 4 благоприятствуют событию А (появление цветного шара) 5 исходов.

События называются равновозможными, если есть основания считать, что не одно из них не является более возможным, чем другое.

Статистическое определение вероятности

Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.

Относительной частотой события А называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:

,

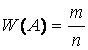где m – число появлений события А, n – общее число испытаний.

17. Виды событий: достоверное, невозможное, случайное.

В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, напри-мер, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра — но при большом количестве бросков число выпадений герба приближается к по-ловине количества бросков; нельзя заранее предсказать результат одного выстрела из дан-ного орудия по данной цели, но при большом числе выстрелов частота попадания прибли-жается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.

Основным интуитивным понятием классической теории вероятностей является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:

а) достоверное событие — событие, которое всегда происходит при проведении опыта;

б) невозможное событие — событие, которое в результате опыта произойти не может;

в) случайное событие — событие, которое может либо произойти, либо не произойти. Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным — выпадение 10 очков, а случайным — выпадение 3 очков.