10. Применение степенных рядов.

1. Степенные ряды м-применятся д/приближ-го вычисления ф-ии. Напр, зная разложение sinx,вычислим знач-е этой ф-ии при с точностью

Т.к ряд знакочередующийся Лейбницевсого типа, то остаток ряда по модулю не превосходит первого отброшенного члена.

Оценим погрешн-ть r_n(x) после образования n-членов ряда

мы должны подобрать такое n,чтобы это все было

В резул-те это неравенство выполняется уже при n=2.

Т.е. sinx≈ c точностью до д/

Разложение ф-ий f(x)=cosx, sinx, , м-использовать д/вычисления этих ф-ий при значе-ях x(т.к эти разлож-я справедливы д/ x с любо степенью точности)

Ряд д/логарифмов хотя и знакопеременный, но сходится медленно, а при x>0 расходится.Поэтому, чтобы ускорить сходимость ряда и сделать возможным вычисление логарифмов чисел x>1 делают ^щее:

Из ряда (1) вычтем ряд (2).

С help ряда (3) сходящегося достаточно быстро можно найти логарифмы всех полагая в нем

Отправляясь от можно последовательно найти логарифмы всех натур-х чисел. Ряд д/arctdx=f(x) можно использовать д/вычисления числа π с любой степенью точности. Полагая в разложении arctgx=1, получаем π/4=1-1/3+1/5-1/7+…

Биномиальное разложение можно использовать для извлечения корней.

2. Разложение ф-ий в ряд может использоваться д/вычисления интегралов не берущихся в конечном виде. Напр, _{, ,}

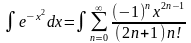
11. Обыкновенным дифференциальным ур-ем(ОДУ) называют ур-ие,связывающее независимую переем X меняющуюся на некот интервале x О неизвестную ф-ию y(x) и её производную , .

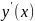В общем виде ОДУ можно записать так: F(x,y, где F-известная ф-ия от (n+1)-переменных.

Порядком ДУ назыв max порядок производной неизв ф-ии входящей в ур-е.

Решением ДУ назыв ф-ия y=φ(x) такая,что при подстановке в данное ур-е получается верное тождество.

Т.о. ОДУ имеет бесконечно много решений.

График решения ДУ назыв интегральной кривой.

Решение ДУ содержащего const С назыв общим решением ДУ. Чтобы выделить единств решение необходимо наложить дополнит усл-е y(x₀)=y₀, кот назыв условием Коши.

Задача Коши(задача с начальным усл-ем). Пусть ф-ия а(чбн) определена в некот области D. (x₀,y₀) . Требуется найти реш-е ур-я F(x,y, , удовлетворяющее усл-ю y(x₀)=y₀

Рассм ДУ 1 порядка F(x,y, (1). Если его можно разрешить относит-о производной, то получим ур-е =f(x,y) (2), кот назыв ур-ем разрешенным относит-о производной. Простейшим видом ур-я = f(x,y) явл =f(x). ; Теорема(существования и единственности решения задачи Коши). Если в области D ф-ия F(x,y) непрерывна и имеет непрерывную частную производную , то (x₀,y₀) в некот открестности т.x₀ единств решение-задача Коши:

12. Ур-ем с разделяющимися переменными назыв ур-е вида где и - непрерывные ф-ии (x₁,x₂), (y₁, y₂). Чтобы найти реш-е этого ур-я необходимо разделить переменные -ур-е с разделенными переменными.После его можно интегрировать и получаем реш-е.

Замеч: При разделении переменных мы делили на ф-ю f₂(y), предполагая,что на соответствующем промежутке она в 0 не обращается. Поэтому,чтобы найти все решения ур-я учитывают и нули ф-ии f₂(y).

К ур-ям с разделяющимися переменными сводятся и ур-я вида: Чтобы свести к ур-ю с разделяющимися переменными сделаем замену тогда . Получим , ; ; .

13. Ф-ия f(x, y) назыв однородной ф-ей k^го-измерения, if при параметре t выполн-ся равенство: f(tx,ty)=t^kf(x,y)

Однородным ур-м 1 порядка назыв ур-е вида , где а(чбн)-однородная ф-ия нулевого измерения.

Однородную ф-ию нулевого измерения всегда можно предстваить в виде f(x,y)=f(x/y). Поэтому однород ур-е-это ур-е вида: . Чтобы свести однородное ур-е к ур-ю с разделяющимися переменными делают замену y/x=t(x). Тогда y=xt(x), . Подставляем в ур-е: ; .

14. К ур-ям сводящимся к однородным относятся ур-я вида: (1). C₁или С₂≠0. Д/того,чтобы свести ур-е (1) к однородному делается замена переменной: где

(2) .Т.о.решая сист-у(2) получаем значение x₀,y₀, т.е. выражения ю При подстановке (3) . Подставляя в (1), получаем, что =f( )=f( )=f(

15. , где a(x) и b(x)- произвольные ф-ии, т.е. линейным ДУ 1порядка назыв ур-е, линейное относит-о неизвестной ф-ии и её производной.

УР-е (1) сводится к двум ур-ям с разделяющимися переменными путем искусств-го приема. Представим неизв ф-ию в виде произв y(x)=U(x)V(x) одной из ф-ий U//V мы можем распоряж как угодно, а 2 ф-ия д-б определена в зависимости от 1 т.о. , чтобы их проиведение удовлетворяло ур-ю (1). Именно, поступают след образом. Решение ищем в виде .

(2) Полагая,что ( , т.е. решая ур-е, кот явл ур-м с разделяющимися переменными. Подставляем найден ф-ию V в ур-е (2), получаем , т.к. V найдена и зависит от x. U=φ(x)+C. Реш-м ур-я (1) формируется из найденных ф-ий y(x)=U(x)V(x).

16. К уравнениям сводящимся к линейным относят ур-е Бернулли. .Чтобы свести это ур-е к линейному обе части делят на yⁿ, т.е. приходят к виду: и делают замену: Z(x)=1/y^n-1, после подстановки Z и получаем: получили ур-е линейное относительно ф-ии Z.

17. Уравнения в полных дифференциалах. Рассм ДУ 1^го порядка,записанное в дифференциале: Р(x,y)dx+Q(x,y)dy=0.(1)/ Предположим,что левая часть ур-я явл полным дифференциалом некто-й ф-ии U(x,y) (тогда du= т.е. P(x,y)= . В этом случае ур(1) назыв ур-ем в полных дифференциалах.

Теорема. Для того,чтобы выражение P(x,y)dx+Q(x,y)dy было полным дифференциалом некот-й ф-ии необходимо и достаточно,чтобы . Т.о. если в ур-ии(1) выполняется усл-е ,то левая часть ур-я явл диф-лом некот-й ф-ии. Значит ур-е (1) .

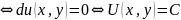18. ДУ 2 порядка.F(x,y, y . В некот-х случаях это ур-е можно разрешить относит-о 2 производ-й y .(2). Простейший случай такого ур-я y

ДУ 2 порядка имеют бесчисленное множество решений,кот задаются формулой y=φ(x, C₁, C₂), т.е. содержит две произвольные постоянные. Эта сов-ть решений назыв общим решением du 2 порядка. Частное решение ур-я (1) отыскивается при помощи задания нач-х решений . Геометрич смысл нач-х условий: Помимо точки (x₀,y₀) через которую должна проходить интегральная кривая, мы ещё задаем угловой коэф касат-й в этой точке к этой кривой.

Замеч.Т.к. общее решение ур-я 2 порядка зависит от двух произвольных постоянных, то через данную точку проходит бесчисл множ-во интегр-х кривых, лишь одна из кот-х имеет заданный угловой коэф-ент.

Теорема существования и единственности решения задачи Коши. Если ф-ия f(x, y, ) непрерывна в корестности значений x₀, y₀, y₀ , то ур-е (2) имеет решение y=y(x), что y(x₀)=y₀, y (x₀)=y₀ Если кроме того непрерывны и частные производные , то данное решение будет единственным.

19. Ур-я 2 порядка допускающие понижение порядка. Рассм ур-е 2 порядка (1) и рассм в каких случаях данные ур-я можно свести к ур-ям 1 порядка, т.е. понизить порядок: а) Правая часть ур-я (1) не содержит y и , т.е. имеем ур-е вида: 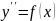Двухкратным интегрированием получаем реш-е данного ур-я: y= б)правая часть ур-я (1) не содержит искомой ф-ии y . Тогда y принимают за новую ф-ию y Получаем z . Из посл ур-я находится ф-ия Z, тогда y= ; в)правая часть ур-я (1) не содержит x. т.е. В этом случае рассм-ют y как независимую переменную и полагают,что y Тогда y , т.е. y =p(y), y .Подставляя в ур-е получим: pp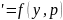 -ур-е 1 порядка относит ф-ии y.т.к. y -интегрируя приходим к решению.

20. Обычно рассматривают ур-я разрешенные относит-о старшей производной: y⁽ⁿ⁾=f(x,y,y .(3) Общее решение ур-я (3) зависит от n произвольных постоянных: y=φ(x,C₁, C₂,..,C_n). Чтобы выделить частное реш-е необходимо задать нач-е условие: . Самый простейший вид y⁽ⁿ⁾=f(x). Проинтегрировав n раз находим общее реш-е. Для ДУ n^го порядка,аналогично пункту 2, справедливо 3 случая понижения порядка.

21. Это ур-е вида: y +a₁(x)y +a₂(x)y=f(x) (1),т.е это ур-е линейное относительно неизвестной ф-ии и её производной, если правая часть f(x)=0, то ур-е называют линейным однородным уравнением.Иначе неоднородным.Если в некот интервале а≤х≤b ф-ии а₁(х),а₂(х) и f(x) непрерывны, то ур-ие(1)при нач-х условиях у(х₀)=у₀, y (x₀)=y (0), y (x₀)=y ₀ имеет единств реш-е удовлетворяющее условиям.Это следует их того,что к ур-ю (1) записанному в виде y =-a₁(x)y -a₁y-f(x) применима теорема о существовании и единственности задачи Коши.Раасмотрим ур-е (1) без правой части,т.е соответствующее однородное ур-е y +a₁(x)y +a₂(x)y=0 (2)

Теорема:Если y₁(x) и y₂(x) какие-л частные решения ур-я(2),то их линейная комбинация y=C₁y₁(x)+C₂y₂(x) тоже будет явл реше-ем ур-я (2) при С1 и С2.

Док-во:Рассмотрим y=C₁y₁(x)+C₂y₂(x). Найдем y =C₁y₁ +C₂y₂ , y =C₁y₁ +C₂y₂ . Подставляем в ур-е: С₁y₁ +C₂y₂ +a₁C₁y₁ +a₁C₂y₂ + a₂C₁y₁+a₂C₂y_2’=C₁(y₁ +a₁y₁ +a₂y₁)+C₂(y₂ +a₁y₂ +a₂y₂)=0.Вывод: если y₁(x) и y₂(x)-решение ур-я (2),такие что y₂/y₁ ≠const,то выражение C₁y₁(x)+C₂y₂(x) будет общим реш-ем ур-я (2),т.е. линейного однородного ур-я.Из общего реш-я при заданных возможных нач-х усл-х м-б найдено частное реш-е,удовлетворяющее начальным.

Пусть задано нач-е усл-е : y(x₀)=y₀, y (x₀)=y₀ , подставляя нач-е условие в общее решение, получим систему относительно C₁ и C₂,а именно : y=C₁y₁+C₂y₂, y =C₁y₁ +C₂y ₂ (3)–сист д/нахождения произвол-х постоянных y₁₀=y₁(x₀), y₂₀=y₂(x₀), y₁₀ =y₁ (x₀), y₂₀ =y₂ (x₀). Чтобы эта система(3) имела единств решение при правых частях необходимо и достаточно,чтобы определитель этой системы был ≠0.

≠0(4) Определитель Вронского

Т.о.,если y₁ и у₂ такие частные решения, что y₂/y₁ ≠const,то определитель(4) будет ≠0 ни в одной точке x₀/

Рассм ур-е с правой частью: y +a₁(x)y +a₂(x)y=f(x) (4) соответствующим ур-ю y +a₁(x) +a₂(x)y=0.

22. Теорема(о структуре общего решения линейного неоднородного ур-я).Общее реш-е линейного неоднородного ур-ия(4) можно составить как сумму общего решения соответствующего однор.ур-ия и какого-л частного решения данного неоднородного.Т.о. общее решение ур-я (4): y_общ=у_{общ.однор+}

23. Линейные однородные ур-я 2^го порядка с постоян-ми коэф:y''+a₁y +a₂y=f(x) (5), a₁, a₂-const. Введем в рассмотр-ие ф-ю y=e^rx , тогда y'=re^rx , y =r²e^rx. Подставим в ур-е (5):r²e^{r x}+a₁re^{r x}+a₂e^{r x}=0, e^rx(r²+a₁r+a₂)=0, e^rx≠ 0. Чтобы ф-я e^rх являлась реш-ем ур-я (5) надо чтобы r²+a₁r+a₂=0 (6). Ур-е (6) явл характеристическим ур-м ур-я (5), чтобы составить характеристическое ур-е нужно заменить у на 1, у'=r, y''=r². В зависимости от того какие корни будут в ур-ии (6) будет выглядеть общее реш-е ур-я (5). Д/корней ур-я (6) возможны 3 случая: 1) r₁≠ r₂, r₁,r₂ R (D>0). Имеем 2 частных реш-я: e^r1x, e^r2x и =>согласно теор, общее реш-е будет иметь вид у=C₁e^r1x+C₂e^r2x, 2) r₁=r₂, r₂,r₁ R(D=0)имеем только1 решение.Покажем,что в качестве 2 реш-я можно взять y₁=e^r1x,y₂=xe^r1x, y₂ =e^r1x+xr₁e^r1x, y₂ =r₁e^r1x+r₁e^r1x+xr₁²e^r1; r₁e^r1x+r₁e^r1x+xr₁²e^r1+a₁e^{r1 x}+a₁xr₁e^{r1 x}+a₂xe^{r1 x}=e^{r1 x}(2r₁+a₁+x(r₁²+a₁r₁+a₂))=0 при 2r₁+a₁=0,т.к r₁-двукратный корень ур-я r²+a₁r+a₂=0,то r₁+r₂=-a₁, 2r₁=-a₁

Т.о. имея 2 линейно независимых частных реш-я можем записать общее реш-е однородного ур-ия. y_общ=С₁е^{r2 x}+C₂xe^{r1 x}, 3)r₁ и r₂ (D<0) комплексно сопряженные корни,т.е. r₁=α+iβ; r₂=α-iß

у₁=e^{(α +iß)х}, y₂=e^(α-iß)x, у_общ.=с₁e^{(α +iß)x}+с₂е^{(α -iß)x}. Чтобы записать это реш-е в действит-й форме применяют формулу Эйлера

e^{i t}=cost+isint, + 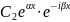; y=e^{α х}(С₁ cos ß х+C₂sin ß х)

Пример: y''+4y'+13y=0 составляем характеристическое ур-е r²+4r+13=0 D=4-13=-9, √(-9)= √(i²3²)=3i, √(-36)= √(-1*36), (α=-2, ß=3), r=-2±3i, y_общ=e^-2x(c₁cos3x+c₂sin3x)

24. y +a₁y +a₁y=f(x) (1), a₁a₂-const.Общее реш-е такого ур-я имеет вид: y_общ=у_{общ.однор.}+ _{-частное решение неоднорого уравнения}.Рассм нахождение частного реш-я по методу неопредел-х коэффиц-ов.Это можно сделать в случае,когда правая часть ур-я (1) имеет спец вид:1)Пусть f(x)имеет вид:f(x)=Pn(x)e^mx, где Р_n(x)-многочлен,m-какое-то R. Тогда частное реш-е ур (1) соответствующее данной правой части будет иметь вид: =Q_n(x)e^mхХ^k, где Q_n(x)-многочлен той же степени что и Рn(x)общ вида,k-кратность корня m в характеристич-м ур-ии соответствующего однор ур-я.

2)Если правая часть ур-я имеет вид: f(x)=acosnx+bsinnx, то частное реш-е,соответствующее этой правой части =Acosnx+Bsinnx, если ±in не явл корнем характ.ур-я, то на хне домножаем. =x(Acosnx+Bsinnx, if in явл кор ур.

3)Если правая часть ур-я имеет вид :f(x)=e^αx(Р_n(x)cosßx+Q_m(x)sinßx), то частное реш-е соответствующее правой части,найдется в виде =e^αx(Ts(x)cosßx+Rs(x)sinß)x^k, где Ts, Rs-многочлены общего вида степени S,кот-я есть max{min}, k-кратность корня α±iß в характеристическом ур-ии.