1.Рассм числовую последоват-ть 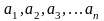(1). Если эта последоват-ть имеет конечную сумму, то сумму членов этой последовательности называют рядом.

Опред: Последоват-ть (1), рассматривая с т.з. 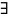^ия суммы её членов называется рядом: 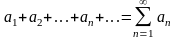(2)

Обозначим 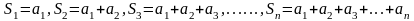n-частичная сумма ряда (3).

Последоват-ть 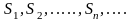назыв-я последоват-тью частичных сумм ряда (2).

Суммой ряда (2) называется предел n-частичной суммы, т.е.

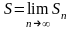
Если сумма ряда и конечна, то ряд назыв сходящимся. В противном случае – расходящимся.Если S-сумма ряда (2), то

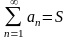
Простейшие свойства рядов:

1. Необходимый признак сходимости ряда. Если ряд сходится, то

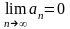
Будем обознач-ть ряд: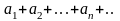 (А), сумму ряда А, а_n-общий член ряда.

Док-во: Если (А) сходится, то 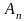частичная сумма , ,

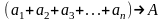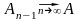2. Ряд,полученный произведением (А) на число «с», т.е. 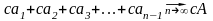сходится или расходится также как и сам ряд А, причем в случае сходимости: S=ca.

Суммой рядов (А) и (В) называется ряд (С) с общим членом .

3. Если (А) и (В) – сходящиея ряды, то ряд (С) тоже сходится, причем С=А+В.

4. Остатком ряда после k^того члена или k^тым остатком называют ряд. 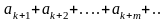Сумму остатка будем обозначать r_k. При 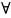kϵN сходимость (А) 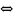сходимости его k-остатка при этом .

Следствие: Вычеркивание из ряда конечного колич-ва слагаемых// вписывание в него конечного колич-ва слагаемых, не влияет на сходимость ряда. При этих операциях достаточно далекие остатки полученного ряда будут является остатками прежнего ряда. А сходимость остатка сходимости ряда.

5. Если (А) сходится, то r_{k .}

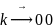2.Ряд (А) называется положительным, если все члены его ряда положительны.

Теорема Коши (достаточный признак сходимости ряда) если сходится ряд А , то сходится и сам ряд (А).

Критерии сходимости положительного ряда.С учетом теоремы Коши при исследовании производного ряда сначала выгодней исслед-ть соответствующий ряд из абсол-ых величин,т.е.положит-го ряда.Если этот ряд сходится,то исходный ряд сходится абсол-но, в противном случае исходной ряд может сходиться//расходится условно.

Теорема 1. Д/положит-го ряда сумма всегда и =: А=sup{A_n}и поэтому ряд сходится, если A_n ограничены сверху и расходится в противном случае.

Замеч: Supremum^ом множ-ва А нызыв наименьшее из верхних границ этого множ-ва т.е: 1) если множества сверху замкнуто

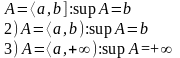множ-во сверху незамкнуто

Неогранич множество.

Доказ-во: Д/положительного ряда последовательность частичных сумм 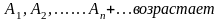т.к.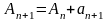 .Поэтому 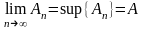а предел = сумма ряда.И 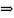,если огранич последов-ть, то 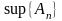конечное число, значит ряд сходится.

Теорема2 (Критерии сходимости):Д/того чтобы (А) сходился необходимо и достаточно, чтобы множество его частичных сумм б. ограничено.

Теоремы сравнения д/положит рядов.Рассм 2 ряда: a и b.

Теор1: Если,начиная с некот номера n₀ выполняется,что a_n≤b_n(*), то из сходимости (В) сход-ть (А).Из расходимости (А) расход-ть(В).

Теор2. Если начиная с некот № n₀ выполн-ся усл-е 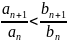(**), то из сход-ти (В) сход-ть(А) и из расходим-ти (А) расх-ть(В).

Теор3. Если 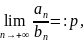то 1)0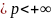 сход-ть (А) сход-ти (В); 2)if p=0, то из сх (В) сх(А),расх(А) расх(В).3)if p=+ ,то из сх(А) сх(В)

3.Абсолютная и условная сходимость ряда.Рассм (А): ,где а_i-люб числа.Сопоставим этому ряду в соответствие ряд из абсол-х величин его членов.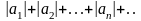 (A )

(А) называется абсолютно сходящимся, если вместе с ним сходится ряд (A ).

Ряд А назыв условно сходящимся,if он сам сходится, а (A ) – расходится.

Знакопеременные ряды.

Рассмотрим (А) члены кот-го м-б как положит-ми так и отрицательными величинами. Такой ряд м-сходится абсолютно// условно либо расходится. При исследовании (А) на абсолютную сходимость рассматривают соответствующий ему ряд из абсол-ых величин: (A )

If (A ) сходится, то исходный (А) сходится абсолютно. Если же (A ) расходится, то исслед-ть сходимость самого (А). Если при этом (А) сходится, а (A ) нет, то это называется условной сходимостью (А). Частным случаем знакопеременных рядов явл знакочередующиеся ряды. (А) называется знакочередующимся,if знак каждого последующего члена ряда противоположен знаку предыдущего. Обозначаем абсолютные величины: .

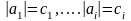_{Знакочередующ} ряд (А):

4.Признак Лейбница: if члены знакочеред ряда по модулю убывают, т.е. 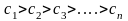>…, , 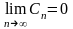то (С) сходится, причем его сумма .

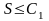Док-во: Рассм послед-ть частичных сумм (С) четного числа членов (n=2m):

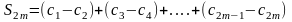. Данная последовательность ,… возрастает и при этом ограничена.

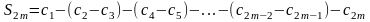-ограничена и .

Согласно теореме о существовании предела монотонной ограниченной последоват-ти ,что последоват-ть имеет предел: 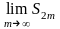=:S

Рассм теперь послед-ть частичных сумм из нечетн колич-ва членов (n=2m+1).

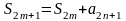. Передем в этом равенстве к пределу:

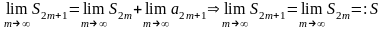т.о S-это сумма ряда; учит-я что , то 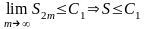. Т.о ряд сх и не превосходит член ряда.

5.Степенные ряды. Радиус сходимости степенного ряда.

Пусть на некотором множестве х задана последовательность функции: 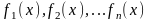.(1). В этом случае говорят, что на множестве Х задана функциональная последовательность. Ряд, членами кот-го явл ф-ии последоват-ти (1) назыв функциональным рядом 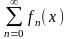(2) Подставляя в (1) любое 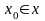получаем числовую последов-сть 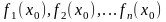при этом ряд 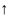будет числовой. 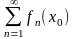. Если этот ряд сходится, то говорят, что ряд (2) сходится в т.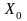 .Областью сходимости ряда (2) называется подмножество из множества Х таких х при которых соответствующий числовой ряд сходится.

Степ ряд-это частный случай функцион-го ряда, члены кот явл ф-ей вида 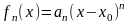Т.о. степ. ряд имеет вид (3),где - центр ряда. При х₀=0 степенной ряд будет записан виде 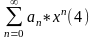. Из вида (3) всегда можно придти к виду (4) заменой на любую переменную z=x-x₀. Будем исследовать степенное ряды в виде (4). Область сходимости степенного ряда: всегда есть не пустое множество т.к. при х=0 ((4)) и х=х₀ ((3)) ряд сходится.

Теорема (о радиусе сходимости степенного ряда):

Д/произв-го степенного ряда вида (4) справедливо:

1. область сходимости Дс этого ряда есть промежуток вида 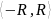, где R≥0

2. число 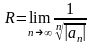или

3. Внутри промежутка сходимости степенной ряд сходится абсолютно.

Замеч:Согласно теореме область сходимости степ-го ряда есть промежуток так что д/уточнения всей области сходимости необходимо отдельно выяснить сходимость ряда в т.х₀ = 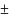R.

6.Свойства степенных рядов.

Теорема 1. Сумма степенного ряда с радиусом сходимости R непрерывна во всех точках его промежутка сходимости.

Св-во2: (О почленном интегрировании).Пусть задан степенной ряд 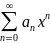и f(x) – его сумма, определенная на Д_c . Степенной ряд допускает почленное интегрирование в интервале сходимости, т.е. д/ х из области сходимости .

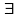(5).

Ряд (5) назыв-т проинтегрированным рядом по отношению к исходному.Он тоже явл степ-м рядом с радиусом сходимости Rⁿ, д/ряда (5) справедливо.

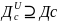
Св-во3:(о почленном дифференц-ии). Д/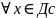 степ ряд допускает почленное дифференцирование, причем 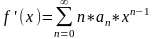(6). Полученный ряд (6) назыв дифференцированным по отношению к исходному и его область сходимости .

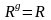Следствие. Степенной ряд внутри промежутка сходимости допускает почленное дифференцирование любое количество раз.

7. Частичные суммы степенного ряда представляют собой многочлены поэтому хорошо вычисляются. Значит удобно при возможности представить ф-ию в виде суммы степенного ряда(//как говорят, разложить функцию ряд).

Пусть f(x) разложимый степенной ряд т.е. коэффи-ты а₀, ,…, и x₀: 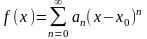. Ясно, что в этом случае, если 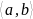с Дс то внутри этого промежутка степенной ряд можно бесконечно дифференцировать.

Необходимое условие разложимости ф-ий в степен ряд явл бесконечн диффер-емость внутри её промежутка.

Рассм ф-ию f(x) в т. . Получим 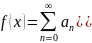.f( )=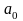 . Продифференцируем ряд (*)

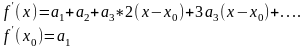(**). Продифференцируем (**)

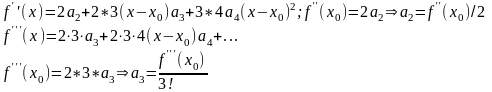
Продолжая процесс получаем, что 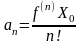- формула д/опред-я коэф-ов при разложении в степенной ряд. Т.о.ряд,в кот разлагается фу-ия, должен иметь вид:

- ряд Тейлора.

Д/ ф-ии бесконечно дифференцируемой в т.х₀ ряд Тейлора . Сходимость ряда в этой точке надо исследовать.

8-9.Теорема(достаточное усл-е разложимости ф-ии в ряд Тейлора):Пусть f(x) непрерывная и непрерывно дифференцируема бесконечное кол-во раз в некот (a,b), причем все n-производные в (a,b) в совок-ти ограничены 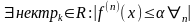тогда ф-ия разложима в ряд Тейлора.

Разложения рассматрив в т.х₀=0(ряд Маклорена).

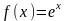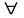Рассм в промеж (-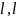 ) 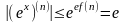т.е достаточное условие разложимости выполнено.

т.е. …

2)Пусть f(x)=sinx. Проверим достаточное условие. В (a,b) 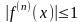x₀=0

f(0)=0 ,

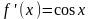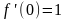
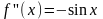
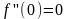
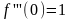
В разложении синуса все слагаемые с четными номерами будут = 0, т.е. будут присутствовать только нечетные степени.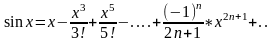 . Аналогично получаем разложение косинуса,в кот-м будут отсутствовать нечетн сетпени,а присутствовать слагаемые с четными степенями будут чередовать знаки.

cosx=1-

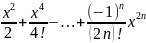
3)f(x)=ln(1+x). Продифференцируем эту ф-ию и разложим по форм геом прогр

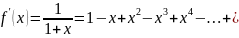
Интегрируя это равенство получим разлож-е исходной ф-ии.

ln(1+x)=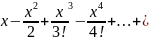

Данное разложение справедливо в промежутке (-1;1]

4) f(x)=arctgx. Продифференцируем и разложим эту ф-ию по форм геом прогр

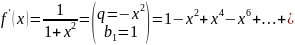
Интегрируя это равенство получаем: arctgx=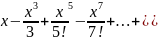

Данное разложение справедливо в [-1,1]. В концевых точ-х сходим-ть усл-ая.

5)Биномиальное разложение. Рассм ф-ию f(x)=(1+x)^α, α≠0. f(0)=1,

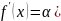
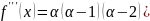
Получаем разложение f(x)=1+α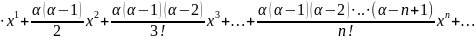 .Данное разложение применимо в интервале (-1,1)