
- •1.2 Основные понятия.
- •Задание.
- •13) Докажите, что следующие формулы являются тавтологиями( законами) алгебры высказываний
- •Как упростить логическую формулу?
- •§ 9. Применение алгебры высказываний для анализа и синтеза переключательных схем
- •Упражнения
- •§2. Функции алгебры логики
- •Оглавление. Введение________________________________________ 3
Упражнения
1. Составить схемы, соответствующие формулам:
а)
![]() ;
;
б)
![]() ;
;
2. Составить формулу, соответствующую схеме, изображенной на рис. 18. .

Рис. 18
3.

Рис.19
4. Упростить формулы, полученные в предыдущих задачах, и построить схемы» соответствующие упрощенным формулам.
6. Построить схему, соответствующую формуле U, заданной таблицей истинности
X |
Y |
Z |
U |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Указание. Образуйте сначала для U СДН-форму.
25. Доказать, что не существует предполных классов, отличных от Сд, Св, L, D (теорема Э. Поста).
26. Доказать, что всякий базис С1 содержит не более четырёх функций.
27. Составить релейно-контактные схемы дли функций.

28. Упростить схемы:




§2. Функции алгебры логики
29. Из контактов х, у, z составить схему так, чтобы она замкнулась тогда и только тогда, когда замкнуты какие-нибудь два из трех контактов х, у, z.
30. Доказать, что в теории множеств

31. Доказать, что в теории множеств

32. Доказать, что в теории множеств
![]()
33. Доказать, что

34. Доказать, что если Zf = U для произвольных множеств
![]()
35. На основании, каких тождеств алгебры логики можно получить следующие теоремы теории множеств?

36. Какие теоремы теории множеств можно получить из следующих тождеств алгебры логики:
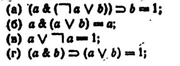
Практическое занятие № 2.
Построить таблицы истинности для следующих функций алгебры логики.
F(x,y,z) = ((x) y) ((x z))
x |
y |
z |
x |
((x) y) |
x z |
(x z) |
F(x,y,z) |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
F(x,y,z) = z → (x y)
x |
y |
z |
x |
y |
x y |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
F(x,y,z) = x y → (x z)
x |
y |
z |
x y |
z |
x z |
(x z) |
F(x,y,z) |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
F(x,y,z) = (x y z) (x y)
x |
y |
z |
z |
x y z |
x |
x y |
F(x,y,z) |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
F(x,y,z) = (x z) y
x |
y |
z |
x |
z |
x z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
F(x,y,z) = (x → y) (y → z)
x |
y |
z |
x |
y |
x → y |
y → z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
F(x,y,z) = (x → y) → z
x |
y |
z |
x → y |
z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
F(x,y,z) = x (y → z) y
x |
y |
z |
y → z |
y |
x (y → z) |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
F(x,y,z) = (x y z)
x |
y |
z |
x y z |
F(x,y,z) |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
F(x,y,z) = (x y) (y z)
x |
y |
z |
x y |
y |
z |
y z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
F(x,y,z) = (x → z) y
x |
y |
z |
x |
z |
x → z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
F(x,y,z) = (y z) → (x z)
x |
y |
z |
y |
z |
y z |
x z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
F(x,y,z) = x → (y z)
x |
y |
z |
y |
z |
y z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
F(x,y,z) = (x → y) (y → x) z
x |
y |
z |
x |
x → y |
y |
y → x |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
F(x,y,z) = z x y
x |
y |
z |
y |
x y |
F(x,y,z) |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
Практическое занятие № 3.
Задача 1. Являются ли формулами выражения, составленные из знаков языка логики высказываний.
((((A → B) C) (C A)) → B)
Решение
Это выражение является формулой, т.к.:
а) на основании пункта 1 переменные А и В являются формулами;
б) выражение (А → В) является формулой;
в) т.к. переменная С на основании пункта 1 есть формула, то выражение С, согласно пункту 2 тоже формула;
г) выражение ((А → В) С) – формула согласно пункту 3;
д) выражение (С А) – формула;
И все анализируемое выражение тоже будет формулой.
Не являются формулами выражения: А→), )А→В) и т.д.
Примечание. В современной литературе иногда разрешают скобки опускать.
Определение. Любая часть формулы называется подформулой данной формулы.
Также сама формула рассматривается как часть самой себя.
Каждая формула логики высказываний превращается в высказывание, если всем, входящих в нее переменным придать значения конкретных элементарных или сложных высказываний. Например, если в формуле (А → В) переменной А придать значение «12 делится на 6», а переменной В – «12 четное число», то получим сложное высказывание: «Если 12 делится на 6, то 12 – четное число».
Если переменная входит в формулу более одного раза, то везде ей нужно придавать одно и то же значение.
Какие из следующих выражений являются формулами алгебры высказываний и определить их значение, если А и В – истина, а С и D – ложь.
(A B) C(D) – не является формулой
(A B) → C = 0
(A → B) C = 1
A B C = 1
(A B) C D = 0
A B C = 1
(A B) → C = 0
A → (C B) – не является формулой
При каких значениях А, В, С, D следующие формулы ложны:
1) (A → B) → (C → D)
Истинны: A, B, C
Ложны: D
2) (A B) → D
Ложны: A, B, D
3) ((A → B) → C) → D
Истинны: B, C
Ложны: A, D
4) A → (B → (C → D))
Истинны: A, B, C
Ложны: D
5) ((A B) → C) → D
Истинны: B, C
Ложны: A, D
6) (A B) (C → D)
Истинны: B, C
Ложны: A, D
7) ((A B) → C) → D
Истинны: C
Ложны: A, B, D
8) A → ((B → C) → D)
Истинны: A, C
Ложны: B, D
9) ((A B)) → (C → D)
Истинны: C
Ложны: A, B, D
10) (A → B) → (C → D)
Истинны: B, D
Ложны: A, C
Примеры неправильных рассуждений:
а) ; б) ; в)
5) Написать логической формулой следующее заключение:
«Если фирма приглашает на работу крупного специалиста в области новейшей технологии (А), то она считает ее привлекательной (В) и разворачивает работы по изменению технологии производства своего традиционного продукта (С) или начинает разработку нового продукта (D).
Конкурирующая фирма пригласила на работу крупного специалиста в области новейшей технологии. Следовательно, она разворачивает работы по изменению технологии производства выпускаемого продукта или разработки нового продукта» Уточнить справедливость данного умозаключения.
С учетом принятых обозначений умозаключение примет вид:
«если А, то (В и (С или D)). А Следовательно, С или D»
Используя логические связки, получим окончательно:
((А → (В (С D))) A) → (C D)
Для проверки правильности умозаключения восстановим схему рассуждения и сравним ее со схемой правила заключения (1).
В соответствии с этим правилом истинно заключение В (С D). Конъюнкция двух высказываний В и (C D) истинна, если истинны оба высказывания. Полагая, что В – истинно (что видно из контекста), истинно также (C D). Таким образом, данное умозаключение верно при истинности В.
6) Записать логической формулой следующее изложение сериала:
«Если Марианна – не дочь дона Педро, то либо Хосе Игнасиас – отец Марианны, либо Луис Альберто – не ее брат. Если Луис Альберто – брат Марианны, то Марианна – дочь дона Педро и Хосе Игнасиас лжет. Если Хосе Игнасиас лжет, то либо Луис Альберто – не брат Марианны, либо Хосе Игнасиас – ее отец. Следовательно, Марианна – дочь дона Педро.
Обозначим
А – Марианна – дочь Педро
В – Луис Альберто не Брат Марианны
С – Хосе Игнасиас – отец Марианны
D – Хосе Игнасиас лжет.
Получим:
(((А) → (С В)) (В → (A D)) (D → (C B)) (A C)) → A
Практическое занятие № 4.
Построить СДНФ.
Упростить выражение, используя известные свойства операций и законы математической логики.
x |
y |
z |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
F1 = (x y z) (x y z) (x y z) = (x y) (y z)
F2 = (x y z) (x y z) (x y z)
F3 = (x y z)
F4 = (x y z) (x y z)
F5 = (x y z) (x y z) (x y z)
F6 = (x y z) (x y z) (x y z)
F7 = (x y z) (x y z) (x y z) (x y z)
F8 = (x y z) (x y z) (x y z)
F9 = (x y z) (x y z)
F10 = (x y z) (x y z) (x y z)
2.16
x (x y z) (x z) = (x x y (x z)) (x z) = (x z) (x z) = = (x z x) (x z z) = x z
2.17
(x y) (y x z) = (x y) (x x z) (y y) (y x z) = (x y) (y x z)
2.18
x (y x) (x z) = (x x) (x z) y = x z y = x y z
2.19
(x → y) x y = (x y) x y = (x x y) (y x y) = 0
2.20
(x y) → (z x) = (x y) (z x) = (x y) (z x) = x y
2.21
(x y z) x z = (x y) x z = x y z
2.22
((x z) (x y)) (z → y) = ((x z) (x y)) (z y) = ((x z) (z y)) ((x y) (z y)) = ((x z z) (x z y)) ((x y z) (x y y)) = = (x z y) (x y z)
2.23
(x y z x y z) x y = (x x y) (y z x y) (x y z x y) = x y
2.24
(x → y) (y → x) = (x y) (y x) = (x y) (x x) (y y) (y x) = = (x y) (y x)
2.25
(x y z x z) y = ((x y z) y) ((x z) y) = x y z
Практическое занятие № 5.
Из прошлого:
Способы задания бинарных операций (из теории множеств)
φ : M x M → M на конечном множестве М = {a1, a2, … , an}
1) Таблицей Кэли
2) Списком всех троек (a, b, c),где a и b – первый и второй аргументы из М, с – результат выполнения операции φ над a и b, a, b, c ∈ M. Для всюду определенной операции число всех троек в списке |M x M| = n2
3) формулой φ(a,b) = с – так называемое префиксное представление операции; иное – инфиксное представление бинарной операции формулой а φ b = c, например
a 3 b = c, где 3 – операция сложения по модулю 3 (результат с выполнения операции 3 равен остатку от деления суммы аргументов (a + b) на 3.
Задача. Логическая функция трех переменных задана формулой в префиксной форме.
f(x1, x2, x3) = f3(f1 (x3, x1), f2(x1, f3(x1, x2)))
Представить f в инфиксной форме, если f1, f2, f3 – бинарные операции, причем f1 - , f2 - , f3 - . Вычислить значение функции на наборе (0, 1, 1), x1=0, x2=1, x3=1.
Решение
1) Из условия задачи видно, что функция f задана в неявном виде (префиксное представление), а представление ее в инфиксной форме предполагает представление ее в явном виде, т.к. дано, что f1 - , f2 - , f3 - .
Даны также исходные значения переменных x1=0, x2=1, x3=1.
2) Для вычисления значения функции f на наборе (0,1,1) запишем f в инфиксной форме, т.е. используя данные связки логических операций.
f(x1, x2, x3) = (x3 x1) (x1 (x1 x2))
или f(0, 1, 1) = (1 0) (0 (0 1)) = 1
Ответ: составное высказывание, которое построено из трех простых высказываний, таких что x1=0, x2=1, x3=1, с помощью логических связок , , истинно.
Самостоятельно
1. Представить префиксные формулы логических функций трех переменных
f(x1, x2, x3) в инфиксной форме, если f1 = , f2 = , f3 = , f4 = и вычислить f на наборах значений.
а) (0,1,1)
б) (1,0,1)
в) (0,1,0)
г) (1,1,0)
1) f1(x3, f3(x1, f2(f4(x1), x2)))
f(x1, x2, x3) = x3 (x1 (x1 x2)))
f(0, 1, 1) = 1 (0 (0 1))) = 1
f(1, 0, 1) = 1 (1 (1 0))) = 1
f(0, 1, 0) = 0 (0 (0 1))) = 1
f(1, 1, 0) = 0 (1 (1 1))) = 1
2) f3(f1(x3, x1), f2(x1,f3(x1, f4(x2))))
f(x1, x2, x3) = ((x3 x1) (x1 (x1 x2)))
f(0, 1, 1) = ((1 0) (0 (0 1))) = 1
f(1, 0, 1) = ((1 1) (1 (1 0))) = 1
f(0, 1, 0) = ((0 0) (0 (0 1))) = 0
f(1, 1, 0) = ((0 1) (1 (1 1))) = 0
3) f3(f4(x1), f1(x2, f2(x3, f3(x1, f4(x3)))))
f(x1, x2, x3) = (x1 (x2 (x3 (x1 x3))))
f(0, 1, 1) = (0 (1 (1 (0 1)))) = 0
f(1, 0, 1) = (1 (0 (1 (1 1)))) = 1
f(0, 1, 0) = (0 (1 (0 (0 0)))) = 0
f(1, 1, 0) = (1 (1 (0 (1 1)))) = 1
Задание 2.
1) (x1 x2) → ((x1 x3) x2)
f(0, 1, 1) = (0 1) → ((0 1) 1) = 1
f(1, 0, 1) = (1 0) → ((1 1) 0) = 1
f(0, 1, 0) = (0 1) → ((0 0) 1) = 1
f(1, 1, 0) = (1 1) → ((1 0) 1) = 1
2) ((x3 x1) x2) → (x1 x3)
f(0, 1, 1) = ((1 1) 1) → (0 1) = 1
f(1, 0, 1) = ((1 0) 0) → (1 1) = 1
f(0, 1, 0) = ((0 1) 1) → (0 0) = 0
f(1, 1, 0) = ((0 0) 1) → (1 0) = 1
3) ((x2 → x3) x1) ((x1 x3) x2)
f(0, 1, 1) = ((1 → 1) 0) ((0 1) 1) = 1
f(1, 0, 1) = ((0 → 1) 1) ((1 1) 0) = 1
f(0, 1, 0) = ((1 → 0) 0) ((0 0) 1) = 0
f(1, 1, 0) = ((1 → 0) 1) ((1 0) 1) = 1
Задание 3. Доказать с использованием таблиц истинности
1) (A → B) и (A B)
A |
B |
B |
A B |
A → B |
(A B) |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
2) (A → B) и (A B)
A |
B |
B |
A B |
A → B |
(A B) |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
3) (A → B) и (A B)
A |
B |
A |
A → B |
A B |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
4) (A B) и (A → B)
A |
B |
A |
A B |
A → B |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
5) (A B) и (A → B) (B → A)
A |
B |
A → B |
B → A |
A B |
(A → B) (B → A) |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
6) (A B) и (A B) (B A)
A |
B |
A |
B |
A B |
B A |
A B |
(A B) (B A) |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
7) (A ≢ B) и (A B)
A |
B |
A B |
A ≢ B |
(A ≢ B) |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
8) (A ≢ B) и (A B) (A B)
A |
B |
A |
B |
A B |
A B |
A ≢ B |
(A B) (A B) |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
(A B) и (A B)
A |
B |
A |
B |
A B |
A B |
(A B) |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
10) (A B) и (A B)
A |
B |
A |
B |
A B |
A B |
(A B) |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
11) (A → B) и (B → A)
A |
B |
A |
B |
A → B |
B → A |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
12) (A B) (A B) и B
A |
B |
A |
A B |
A B |
(A B) (A B) |
B |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
13) A (A B) и A
A |
B |
A B |
A (A B) |
A |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
14) A (A B) и A
A |
B |
A B |
A (A B) |
A |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Практическое занятие № 6.
Задание 1. При каких значениях переменных x, y, z. Следующие формулы истины и ложны.
а) (((x → (y z)) → (y → x)) → y) = (((x (y z)) → (y x)) → y) = ( ((x (y z)) (y x)) → y) = (((x (y z)) (y x)) y) = (x (y z) (y x)) y = ((x (y z) (y x)) y) = x y
x |
y |
x |
y |
x y |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
б) (((x y) z) → ((x y) (x z))) = (((x y) z) ((x y) (x z))) = ((x y z) x (y z))
x |
y |
z |
x |
y |
z |
x y z |
y z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
г) (((x y) ((y z) (z x))) → ((x y) z)) = ((x y) ((y z) (z x))) ((x y) z) = (x y) (y z) (z x) (x y z) = (x y) (y z) (z x) (x y z)
x |
y |
z |
x |
y |
z |
x y |
y z |
x z |
x y z |
F(x,y,z) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Задание 2. Являются ли тождественно истинными
1) A → (B → (A B)) = A (B (A B)) = A (B A) = 1 B = 1 -является
2) (A B) ≢ (A → B) = ((A B) (A B)) ((A B) (A B)) = (A (B B)) (A B A B) = A 1 = A – не является
3) (A → (B → C)) → ((A → B) → (A → C)) = (A (B C)) ((A B) (A C)) = (A B C) (A B) A C = (A B C) A B C = (A B C) A B C = (A B C) (A B C) = 1 – является
4) (A → (B → C)) → ((B → A) → (C → A) ) = (A (B C)) (B A) C A = (A B C) (B A) C A = (A B C) A B C = C (A B) A B = A B C
Задание 3. Привести к КНФ и проверить, являются ли они тождественно истинными.
1) A → ((A → B) → B) = A ((A B) B) = A (A B) B = A (A B) B = A (A B) = 1 B = 1 = (A A B) - является
2) ((A → B) (C → D)) → ((A C ) → (B D)) = ((A B) (C D)) ((A C) (B D)) = (A B) (C D) A C (B D) = A B C D B D = A B C D C D = 1 = (A B C D D) – является
3) (A → B) → ((A C) → (A C)) = (A B) ((A C) (A C)) = (A B) 1 = 1 = ((A B) 0)
4) (A → (B C)) → ((A → B) (A → C)) = (A (B C) ((A B) (A C)) = (A (B C)) A (B C) = 1 – является
5) ((A → B) (A → C)) → (A → (A C)) = ((A B) (A C)) (A A C)= = (A B C) 1 = 1 – является
Задание 4. Упростить
1) ((A B) → (B C) ) ((B B) → (B → C)) = ((A B) B C) (B B C) = (A B B C) (B C) = B C
2) ((A B) → (A C)) ((B C) → (A B)) = ((A B) A C) ((B C) A B) = (A B C) (A B C) = A (A B) (A C) (A B) (B C) (A C) (B C) = A (B C) (B C)
Практическое занятие № 7.
Привести к ДНФ и КНФ:
а) (((A → B) → (C → A)) → (B → C)) = (((A B) (C A)) (B C) = ((A B) (C A)) B C = (A B C) B C = (A C) (B C) (C C) B = (A C) (B C) B = C (A B) B = B C = (B C)
б) (((((A → B) → A) → B) → C) → C) =((((A B) A) B) C) C = = ((((A B) A) B) C) C = ((((A B) A) B) C) C = ((((A B) A) B) C) C = (((A B) B) C) C) = (((A B) B) C) C = ((A B) C) C = C – для ДНФ и КНФ
в) ((A → (B → C)) → ((A → C) → (A → B))) = (A (B C)) ((A C) (A B)) = (A B C) (A C) A B = A ((B C) C) A B = A (C B) A B = (A C) (A B) A B – ДНФ
КНФ: (((A C) (A B) A B)) = ((A C) (A B) A B)
Задание 2.
а) ((A → B) → ((B C) → (A C))) = (A B) (B C) (A C) = (A B) (B C) (A C) = (A B) B C (A C) = (B A) (C A) = 1
КНФ: 0
б) (((A → B) → A) → (A → (B A))) = ((A B) A) (A (B A)) = = ((A B) A) A (B A) = (A B) A (B A) = A (B A) = A B
в) (((A B) → A) ((A B) → B)) = ((A B) A) ((A B) B) = = (A B) A (A B) B = A B
Задание. Привести к СКНФ
а) (C → A) → ((B C) → A) = (C A) ((B C) A) = (C A) A B C = A B C
б) (((A B) → A) (A (B C)) = ((A B) A) (A (B C)) = ((A B) A) (A (B C)) = A (B C) = (A B) (A B) (A B С) (A B C) = (A B C) (A B C) (A B C) (A B C) (A B C) (A B C) = (A B C) (A B C) (A B C) (A B C) (A B C)
в) (A (B C)) → ((A B) C) = (A (B C)) ((A B) C) = (A B) (A C) (A B) C = (A B) C = (A C) (B C) = (A B C) (A B C) (A B C) (A B C) = (A B C) (A B C) (A B C)
Практическое занятие № 8.
Задание 1. Доказать эквивалентность.
(A (B C)) ((A B) C) = (A B C) (A B C)
(A (B C)) ((A B) (A C)) = (A (B C)) (A (B C))
(A (B A)) A = ((A B) A) A = A A
(A B) (A B) = (A B) (A B)
(A → B) (A B) = (A B) (A B) = (A B) (A B)
(A B) (A B) = (A B) (A B)
(A (B B)) A = (A 1) A = A A
(A (B B)) A = (A 0) A = A A
(A → A) A = (A A) A = A A
((A B) (A C) (B D) (C D)) ((A D) (B C)) = ((B (A D)) (C (A D)) ((A D) (B C)) = ((A D) (B C)) ((A D) (B C))
(A (A C) (B C)) ((A B) (A C)) = (A (C (A B))) ((A B) (A C)) = ((A C) (A (A B))) ((A B) (A C)) = ((A B) (A C)) ((A B) (A C))
Задание 2. Построить формулу и такую, чтобы данная формула была тождественно истинной: (((U Q) → P) → ((P → Q) → U))
Решение.
(((R → (Q P)) → U) → (U (P → Q) R))
Задание 3(38). Построить формулу от трех переменных, которая истинна в том и только в том случае, когда две переменные ложны.
Решение.
A |
B |
C |
F |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
F(A, B, C) = (A B C) (A B C) (A B C)
Задание 4(39). Построить формулу от трех переменных, которая принимает такое же значение, как и большинство (меньшинство) переменных.
Решение.
A |
B |
C |
F1 |
F2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
F1 = (A B C) (A B C) (A B C) (A B C)
F2 = (A B C) (A B C) (A B C) (A B C) = F1
Практическое занятие № 9.
Предикаты.
Переменная, на которую навешан квантор, называется связанной.
Задача 1.
Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы: ∀х Р(х)
Решение.
Это выражение означает – все люди смертны.
Для всех х (людей) Р(х) – истина.
Оно не зависит от переменой х (не важно, кто именно), а характеризует всех людей в целом, т.е. выражает суждение относительно всех х множества М.
Задача 2.
Пусть Р(х) – предикат, «х – четное число», определенный на множестве М. Дать словесную формулировку высказыванию ∃х Р(х), определить его истинность
Решение.
Исходный предикат Р(х), «х – четное число», является переменным высказыванием. При подстановке конкретного числа вместо переменной х он превращается в простое высказывание, являющееся истинным или ложным. Например, если подставить 5, высказывание превращается: «5 – четное число», и оно является ложным.
Высказывание ∃х Р(х) означает: «В М существует четное число». Т.к. множество М, на котором задан предикат Р(х), не определено в условии (тогда говорят, что задача некорректна), доопределим М.
Пусть предикат Р(х) определен на множестве натуральных чисел N, то есть х ∈ N, тогда высказывание ∃х Р(х) истинно (т.к. в N существует обязательно четное число). В общем случае высказывание ∃х Р(х) истинно на любом множестве М, содержащем хотя бы одно четное число, и ложно на любом множестве нечетных чисел.
Задача 3.
Пусть N(х) – предика, «х – натуральное число». Рассмотреть варианты навешивания кванторов. Проинтерпретировать полученные высказывания и определить их истинность.
Решение.
∀х N(x) – высказывание «все числа – натуральные» истинно на любом множестве натуральных чисел, и ложно, если М содержит хотя бы одно ненатуральное число, например, целое отрицательное число.
∃х N(х) – высказывание «существует натуральное х» истинно на любом множестве М, содержащем хотя бы одно натуральное число, и ложно в противном случае.
Задача 4.
Записать предикатной формулой предложение «любой человек имеет отца»
Решение.
Для построения предикатной формулы используем два предиката:
«х – человек»
«у – отец х»
и для удобства восприятия обозначим их ЧЕЛ(х) и ОТЕЦ(у, х). Тогда предложение «любой человек имеет отца» в предикатной форме имеет вид
∀х (ЧЕЛ(х) → ∃у ОТЕЦ(у, х))
Заметим, что если предикат ОТЕЦ(х, у) определен на множестве людей, то можно записать проще:
∀х ∃у ОТЕЦ(у, х)
Литература.
Г.Г. Асеев, О.М. Абрамов, Д.Э. Ситников. Дискретная математика. Ростов-н/Д: Торсинг, 2003-144с.
И.Н. Бродский. Элементарное введение в символическую логику. Изд-во ЛГУ,1972-63с.
А.Д.Гетманова. Учебник по логике. М.:ВЛАДОС,1994-303с.
В
85
.А. Горбатов, А.В. Горбатов, М.В. Горбатов. Дискретная математика. М.: АСТ, Астрель, 2003-447с.Г.И. Москинова. Дискретная математика. М.: Логос, 2002-240с.
Ф.А. Новиков. Дискретная математика для программистов. СПб.: Питер, 2002-304с.
Н.П. Редькин. Дискретная мтематика. СПб.: Лань, 2003-96с.
