Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Камская Государственная Инженерно-Экономическая Академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsii_po_matlogike_dlya_zaoch_a4_dopolnenia_1...doc

Скачиваний:

Добавлен:

24.09.2019

Размер:

1.62 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Как упростить логическую формулу?

Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.

Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).

1)тождества

2) Идемпотентности ,

3)Коммутативности ,

4)Ассоциативности ,

5)Дистрибутивности

6)двойного отрицания

7)де Моргана ,

8) , , ,

9)Противоречия

10)исключенного третьего

11)замены эквиваленции

12)поглощения

13)склеивания

14)контропозиции

15)силлогизма

16)прямого вывода (заключения)

17)замена импликаций

Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:

1) (законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);

2) (применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);

3) (повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);

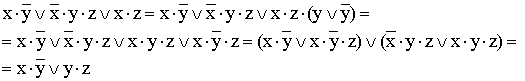(вводится вспомогательный логический сомножитель ( ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);

5) (сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);

6) (выносятся за скобки общие множители; применяется правило операций с константами);

7) 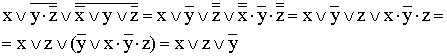(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);

8) 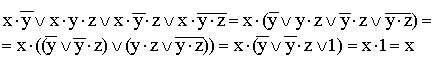(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции применяется правило операции переменной с её инверсией);

9) 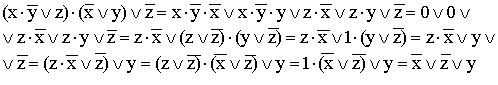(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);

10) 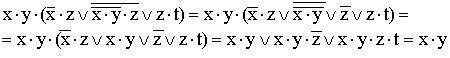(используются правило де Моргана, закон двойного отрицания и закон поглощения).

Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.

Х1	Х2	Φ₀	Φ₁	Φ₂	Φ₃	Φ₄	Φ₅	Φ₆	Φ₇	Φ₈	Φ₉	Φ₁₀	Φ₁₁	Φ₁₂	Φ₁₃	Φ₁₄	Φ₁₅
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	0	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
		0	Λ		Х1		Х2			↓	~		←		→	│	1
		Константа 0	Конъюнкция «и»		Переменная х1		Переменная х2	Сложение по модулю 2(раздел.смысл)	Дизъюнкция «или»	Стрелка Пирса(конъюнкц.отрицаний)	эквивалентность	Отрицание х2		Отрицание х1	импликация	Штрих Шеффера(х1, х2 не совместимы)	Константа 1

1.4. Булева алгебра. Совершенная дизъюнктивная нормальная форма (СДНФ).

Одна и та же логическая функция может быть задана формулами, включающими наборы логических операций.

│

Наборы логических функций (операций), с помощью которых можно выразить любые другие логические функции, называются функционально полными системами, или базисами. Примеры таких систем: , , , , , , .

Лучше всего изучен базис .

Формулы называются булевыми, если они содержат переменные, скобки и знаки функций .

Теорема: Всякая логическая функция может быть представлена булевой формулой, т.е. как суперпозиция дизъюнкций, конъюнкций и отрицания.

Чтобы перейти от табличного задания логической функции к булевой формуле, надо:

1. Для каждого набора значений переменных x₁,…x_n, на которых функция f(x₁,…x_n)=1, выписываются конъюнкции всех переменных; над теми переменными, которые на этом наборе равны нулю, ставится отрицание.

2.Все такие конъюнкции соединяются знаками дизъюнкции.

Полученная таким образом формула называется СДНФ логической функции f(x₁,…x_n)=1.

Для каждой функции СДНФ единственна (с точностью до перестановок переменных или конъюнкций).

Упрощение формул.

Для упрощения формул можно использовать эквивалентные соотношения, выводимые из основных с помощью эквивалентных преобразований:

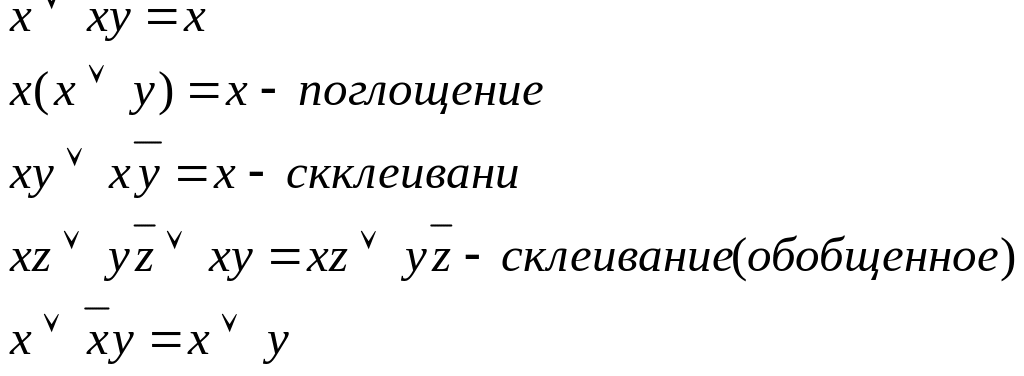
Приведение к дизъюнктивной нормальной форме (ДНФ).

Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.

Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций.

Термин «нормальная» означает, что в данном выражении отсутствуют групповые инверсии, т.е. инверсия над несколькими переменными сразу. Пример ДНФ

Совершенная дизъюнктивная нормальная форма (СДНФ) – это ДНФ, содержащая все полные элементарные конъюнкции данной булевой функции, в которой нет одинаковых элементарных конъюнкций, и каждая из них содержит все переменные данной булевой функции, причем каждую переменную – только один раз ( включая вхождения с отрицанием или без отрицания).

Этапы приведения к ДНФ:

1. Все отрицания «опустить» до переменных с помощью формул:

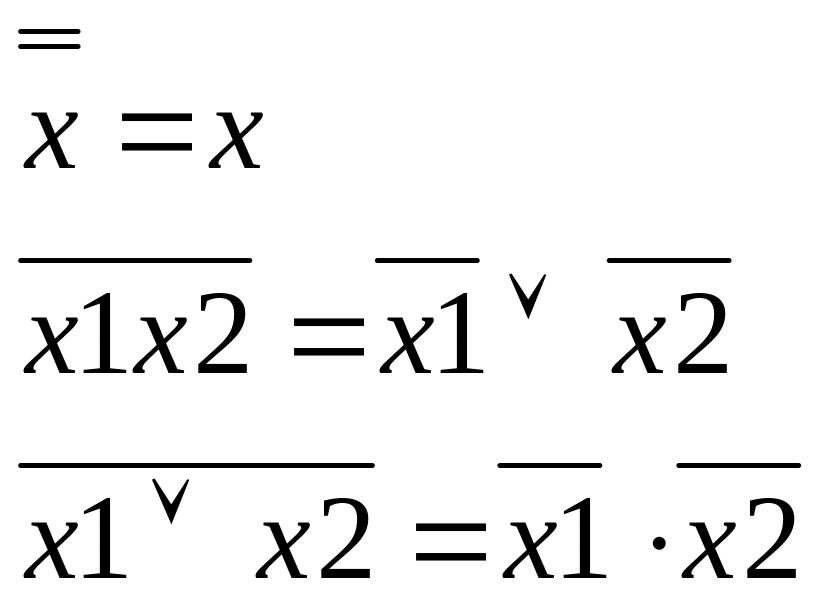
2. Раскрыть скобки с помощью формул:

а) ассоциативности коъюнкций и дизъюнкций:

б) дистрибутивности дизъюнкции относительно конъюнкции:

3. Удалить лишние конъюнкции и повторения переменных в конъюнкциях с помощью формул идемпотентности:

Закона противоречия: .

Закона исключения третьего: .

4. Удалить константы с помощью формул:

Свойства констант (ноль и единица):

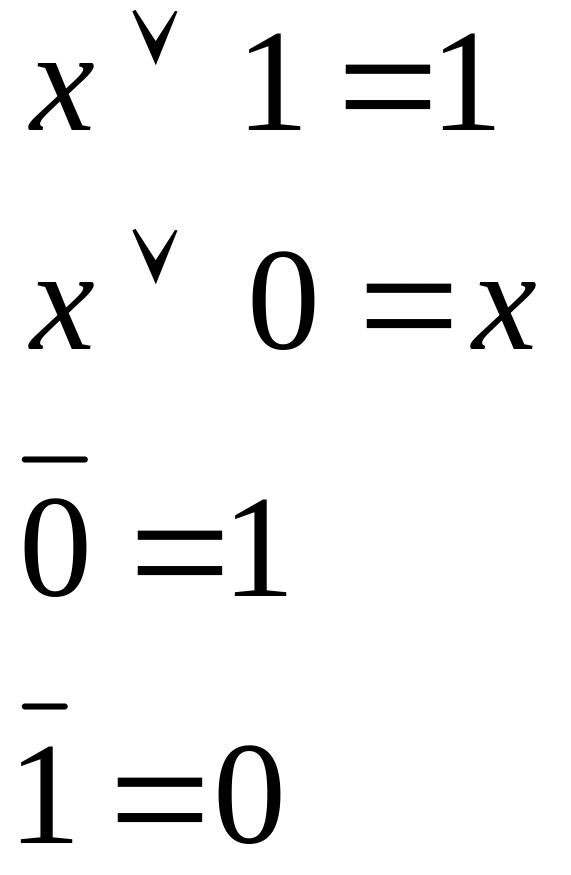
Процедура приведения ДНФ к СДНФ состоит в расщеплении (обратном склеивании: использовании в обратную сторону) конъюнкций, которые содержат не все переменные.

1.6. Приведение к коньюнктивной нормальной форме (КНФ).

Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.

КНФ – конъюнкция элементарных дизъюнкций.

Этапы приведения ДНФ к КНФ:

Пусть ДНФ , где k1,…km – элементарные конъюнкции.

1.Применить к F правило двойного отрицания и привести к ДНФ.

2.С помощью правил деМоргана освободиться от второго отрицания и преобразовать отрицания элементарных конъюнкций в элементарные дизъюнкции.

СКНФ называется КНФ, каждая элементарная дизъюнкция которой содержит все переменные с отрицанием или без него.

Совершенная конъюнктивная нормальная форма (СКНФ) – это КНФ, содержащая все полные элементарные дизъюнкции данной булевой функции, в которой нет одинаковых элементарных дизъюнкций , и каждая из них содержит все переменные данной булевой функции, причем каждую переменную – только один раз ( включая вхождения с отрицанием или без отрицания).

Примеры выполнения упражнения тренинга на умение №2

Задание.

Записать в форме СНДФ функцию , заданную таблицей.