§5.8. Дифференциалы высших порядков (в.П.).

Пусть функцияимеет конечные производные всех требуемых порядков. Тогда(1), где

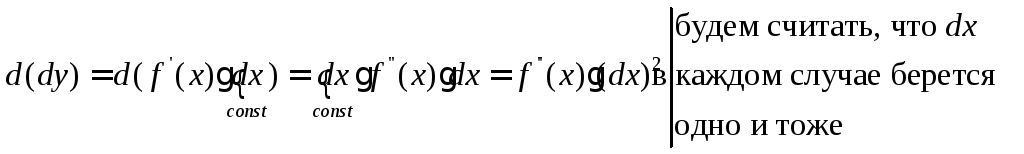
Итак, получаем

Взяв дифференциал -ое количество раз, получаем-ый дифференциал

Лекция №11

Отсутствие инвариантности дифференциала высших порядков.

Рассмотрим функцию В силу инвариантности первого дифференциала дифференциал функциипоможно вычислить как для случая, если быбыла окончательной переменной, где, т.е.-это функция от.

(2)

Если формулу (2) сравнить с формулой для второго дифференциала , видим, что второе слагаемое является лишним, из-за чегоне совпадает с формулой для второго дифференциала, когдабыла бы окончательной переменной. Таким образом, инвариантность для дифференциалов высших порядков отсутствует.

§4. Основные теоремы дифференциального исчисления.

§4.1. Теорема Ферма.

Определение.Пусть. Функцияназывается строго возрастающей (строго убывающей) в точкеотносительно, если существует окрестность этой точкидлявыполняется, что, а длявыполняется. Случай простого возрастания (убывания) аналогичный, только знаки будут нестрогими.

Лемма.

Если внутренняя точка области определения, то прифункциявозрастает в точке(убывает).

Доказательство:

По условию

числитель и знаменатель имеют одинаковые знаки.

Замечание.Лемма доказана для внутренних точек. Если бы речь шла о краевых точках, то лемма тоже сохранялась бы, но возрастание и убывание будут односторонними.

Теорема Ферма(о нуле производной).

Если функция определена на промежуткеи принимает наибольшее (наименьшее) значение в этом промежутке в некоторой точке, то производная в этой точке равна нулю при условии её существования.

Доказательство:

На основе леммы.

Пусть в точке наибольшее значение функции, т.е.(*)длясуществует производная.

Доказательство от противного: пусть , то по лемме

(1)

Если , то по лемме(2)

1. и (2) противоречат условию (*)

§6.2. Теорема Ролля

Теорема Ролля.

1)непрерывна на

2)в

3)

тогда

Доказательство:

По теореме Вейерштрасса-наибольшее значение функции,-наименьшее значение функции, тогда по условию (3) хотя бы одно из этих значений принимается внутри промежутка, назовем эту точкуи по теореме Ферма следует, что.

Геометрический смысл теоремы: Если крайние ординаты кривойравны, то найдется точка, где касательная параллельна оси.

§6.3. Теорема Лагранжа.

Теорема.

Если:

1) непрерывна на

2) в

тогда существует точка (1)

Теорема Роля является частным случаем теоремы Лагранжа, т.к. , тогда.

Геометрический смысл:

геометрически означает, что угол наклона касательной в точкеравен углу наклона хорды.

Формулу (1) называют формулой конечных приращений Лагранжа и записывают в виде: (1)

§6.4. Теорема Коши о конечных приращениях.

Теорема.

Пусть функция и:

1. непрерывны в

2. имеют конечные производные ив

3. и конечна

тогда существует точка (1)

Теорема Лагранжа – это частный случай теоремы Коши, которая получается, если .

Доказательство:

а) сначала покажем, что, т.е.. Если допустить противное:, то функцияудовлетворяет условиям теоремы Роля, а это противоречит условию (3)

б) введем вспомогательную функцию Утверждается, что данная функция удовлетворяет условиям теоремы Роля

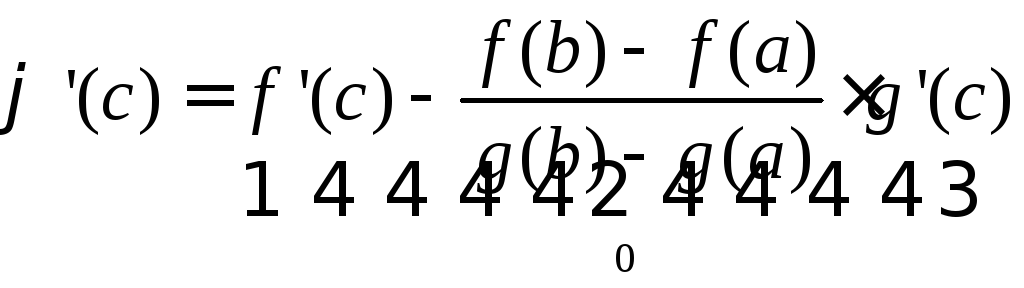, т.е. получена формула (1)

В литературе все рассмотренные теоремы: Ферма, Роля, Лагранжа и Коши – называются теоремами о среднем.