20. Работа в термодинамике.

Механическая работа определяется как:

,

где   — сила, а   — элементарное (бесконечно малое) перемещение.

Элементарная работа термодинамической системы над внешней средой может быть вычислена так:

,

где   — нормаль элементарной (бесконечно малой) площадки,   — давление и   — бесконечно малое приращение объёма.

Работа в термодинамическом процессе  , таким образом, выражается так:

.

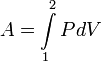Величина работы зависит от пути, по которому термодинамическая система переходит из состояния   в состояние  , и не является функцией состояния системы. Такие величины называют функциями процесса.

Несмотря на то, что до сих пор и в физической химии используется обозначение работы A, в соответствии с рекомендациями ИЮПАК работу в химической термодинамике следует обозначать как W^[1

Изотермический процесс (от др.-греч. ἴσος «равный» и θέρμη «жар») — термодинамический процесс, происходящий в физической системе при постоянной температуре.

В идеальном газе при изотермическом процессе произведение давления на объём постоянно (закон Бойля-Мариотта). Изотермы идеального газа в координатах   — гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс

Работа, совершенная идеальным газом в изотермическом процессе, равна  , где   — число частиц газа,   — температура,   и   — объём газа в начале и конце процесса,   — постоянная Больцмана .

В твёрдом теле и большинстве жидкостей изотермические процессы очень мало изменяют объём тела, если только не происходит фазовый переход.

Первый закон термодинамики для изотермического процесса записывается в виде:

    

Изохорический или изохорный процесс (от др.-греч. ἴσος «равный» и χώρος «место») — термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма.

Из определения работы следует, что изменение работы при изохорном процессе равно:

Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:

,

Но такой интеграл равен нулю. Итак, при изохорном процессе газ работы не совершает:

.

Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю.

Изменение внутренней энергии идеального газа можно найти по формуле:

,

где i — число степеней свободы, которое зависит от количества атомов в молекуле (3 для одноатомной (например, неон), 5 для двухатомной (например, кислород) и 6 для трёхатомной и более (например, молекула водяного пара)).

Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:

,

где   — молярная теплоёмкость при постоянном объёме.

Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:

Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:

,

то есть вся теплота, которую получает газ идёт на изменение его внутренней энергии.

Изобарный процесс (др.-греч. ἴσος «одинаковый» и βάρος «тяжесть») — термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа.

Согласно закону Гей-Люссака, при изобарном процессе в идеальном газе  .

Работа, совершаемая газом при расширении или сжатии газа, равна  .

Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии:  .

Физический смысл универсальной газовой постоянной

ной Больцмана к:

R = N_Ak.

Постоянные Л\ и к имеют ясный смысл: N_a — это число молекул или атомов в единице количества веще­ства, то есть моле; к — постоянная, определяющая связь между темпе­ратурой в кельвинах и температурой в единицах энергии. Но определен­ный физический смысл (быть может, многим он покажется неожиданным) имеет и комбинация N_A и k — посто­янная R.

Представим себе, что I моль иде­ального газа находится в сосуде с подвижным поршнем и что подводом тепла к нему или отводом тепла от него его температуру изменяют на 1 кельвин. Благодаря тому, что сосуд закрыт подвижным поршнем, давле­ние газа будет оставаться постоян­ным (нравным внешнему давлению).

Напишем уравнение состояния га­за до и после нагревания: до нагревания pV_x = RT_% после нагревания pV₂ = R (Т+АТ), где ДТ = 1 К. Вычтя первое равенство из второго, мы получим p(y₂-V_x)=RT + RAT-RT = RtbT.

Левая часть этого равенства пред­ставляет собой работу, совершаемую силой давления газа (или внешней силой против силы давления), когда при постоянном давлении р объем га­за увеличивается (или уменьшается) от V, до V₇.' Следовательно, газовая постоянная R равна работе, которую совершает 1 моль идеального газа, расширяясь при нагревании на 1 К при постоянном давлении.

Разумеется, при изобарном охлаж­дении 1 моля газа на 1 К такую же работу совершает внешняя сила, дей­ствующая на поршень.

(1)

В уравнение состояния идеального газа (уравнение Менделеева — Кла­пейрона)

PV-2RT

входит универсальная газовая по­стоянная R. Она, как известно, равна произведению двух других постоян­ных — числа Авогадро N_A