10. Производная и дифференциал функции одной и нескольких переменных. Достаточные условия дифференцируемости. Правила дифференцирования. Приближенные вычисления с помощью дифференциала.

Одна пер-я.

Пусть фун-я y = f(x) определена в некот. окрестности т. x₀.

Если сущ-ет предел отношения приращения фун-и Δy = f(x₀ + Δx) − f(x₀) к вызвавшему его приращению арг-та Δx, когда Δx → 0, то этот предел наз-ся производной функции y = f(x) в точке x0 и обозн-ся символом f '(x₀), т.е.

f '(x₀) = =

другие обозначения: y '(x), y 'x, ,

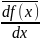
Если указанный предел сущ-ет, то фун-я f(x) является дифференцируемой в точке x. Операция нахождения производной называется дифференцированием. Дифференциалом фун-и y = f(x) наз-ся главная лин. относительно Dx часть приращения Dy, равная произведению производной на приращение независимой переменной dy = f'(x)Dx.

Несколько переменных.

Частной производной от функции по независимой переменной х называется производная , вычисленная при постоянном у.

Частной производной по y называется производная , вычисленная при постоянном х.

Пример.

Рассматривая как постоянную величину у, получим .

Рассматривая как постоянную величину х, получим .

Достат.условия:

Фун-я f(x) наз-ся диф-мой в точке x, если приращение Dy этой фун-и в точке x представимо в виде Dy =ADx +a (Dx) Dx, (1)

где A – некот. число, не зависящее от Dx, а limDx→ 0 a(Dx ) = 0.

Рав-во (1) можно переписать иначе, так как функции a (Dx), Dx - бесконечно малые в точке Dx = 0 и их произведение тоже бесконечно малая функция, поэтому Dy =ADx +o(Dx). (2)

Справедлива теорема

Теорема. Для того чтобы функция была дифференцируема в точке x, необх-мо и достаточно, чтобы она имела в этой точке конечную производную.

Док-во. Необх-ть. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на Dx≠ 0 получим

Dy/Dx = A+a(Dx).

Переходя к пределу в последнем выражении при Dx→ 0, получим, что A=f'(x).

Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел

limDx→ 0Dy/Dx = f'(x).

Обозн-м a(Dx) = Dy/ Dx-f'(x). Отсюда вытекает представление (1).

Достаточное условие дифф-сти функции m переменных.

Пусть функция f( ) определена в некоторой окрестности точки . Пусть у функции в этой окрестности существуют непрерывные частные производные по всем переменным, тогда функция f дифференцируема в этой точке.

Если С – конст. и u=u(x), v=v(x) – некот. диф-мые фун-и, то справ-вы след. правила диф-ния:

1) (C)'=0

2) (x)'=1

3) (u±v)'=u'±v'

4) (Cu)'=Cu'

5) (uv)'=u'v+uv'

6)

7)

8) если y=f(u), u=φ(x) , т.е. y=f(φ(x)) - сложная фун-я, составл-я из диф-мых фун-й, то y'x=y'uu'x или ; То есть производная слож.фун-и = произв-ю ее произв-й по промежуточному аргументу на произв-ю промеж. арг-та по независимой переменой.

9) если для фун-и y=f(x) сущ-ет обратная диф-ая фун-я x=p(y) и , то f'(x)=1/p'(y).

Таблица производных.

(ua(x))' = a ua-1(x)u'(x), в частности,

(1/u(x))' = -u'(x)/u2(x), ( )' = u'(x)/2 ;

(logau(x))' = (u'(x)logae)/u(x) при 0<a№1, u(x)>0, в частности, (ln u(x))' = u'(x)/u(x);

(au(x))' = au(x)ln a u'(x) при 0<a№1, в частности, (eu(x))' = u'(x)eu(x);

(sin u(x))' = cos u(x)u'(x);

(cos u(x))' = -sin u(x)u'(x);

(tg u(x))' = u'(x)/cos2u(x) x№ p/2+p n, n=0,+-1,...;

(ctg u(x))' = -u'(x)/sin2u(x) x№ p n, n=0,+-1,...;

(arcsin u(x))' = u'(x)/ , -1<u(x)<1;

(arccos u(x))' = -u'(x)/ , -1<u(x)<1;

(arctg u(x))' = u'(x)/(1+u2(x));

(arcctg u(x))' = -u'(x)/(1+u2(x)).

11.Геом. смысл пр-ной. Рассм. график фун-и y = f ( x ):

Из рис. видно, что для любых двух точек A и B графика функции:

где - угол наклона секущей AB.

Т. О., разностное отношение = угловому коэф-ту секущей. Если зафиксировать т. A и двигать по направлению к ней т.B, то неограниченно уменьшается и приближается к 0, а секущая АВ прибл-ся к касат-ой АС. =>, предел разностного отношения = угловому коэф-ту касательной в т. A. => произв-ая фун-и в точке есть угловой коэф-т касательной к графику этой фун-и в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику фун-и в т. A (x₀, f (x₀)). В общем случае ур-ие прямой с угловым коэф-том f’(х₀) имеет вид:

y=f’(x₀)·x+b .

Чтобы найти b, восп-емся тем, что касат-я проходит через т. A:

f(x₀)=f’(x₀)·x₀+b ,

отсюда, b = f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо b, мы получим ур-е касат-ой:

y=f(x₀)+f’(x₀)·(x – x₀).

Механ. смысл произ-ой. Рассм. простейший случай: движение матер. точки вдоль корд.оси, причём закон движ-я задан: координата x движущейся точки – известная фун-я x(t) времени t. В течение интервала времени от t₀ до t₀+ точка перемещается на расстояние: x(t₀+ )-x(t₀)= , а её средняя скорость равна: v_a = / . При 0 значение сред. ск-ти к опред. величине, кот. наз-ся мгновенной скоростью v(t₀) материальной точки в момент времени t₀. Но по определению производной мы имеем:

отсюда, v(t₀)=x’(t₀), т.e. скорость – это произв-я корд-ты по времени. В этом и состоит мех. смысл пр-ной. Аналогично, ускорение – это производная скорости по времени: a=v’(t).

Эластичность спроса.

Эл-ть есть мера изменения зависимой переменной в ответ на изменение независимой переменной.

Пусть y(x) –фун-я, харак-щая, напр., издержки произв-ва, где x – кол-во выпуск. продукции. Тогда отношение y(x)/x описывает сред. издержки, прих-еся на одно изделие. Сред. величина обозн-ся Ay или Af. Сред. Приращ-е, сред. прирост, сред. скорость изменения опред-ся отношением Dy/Dx.

Производная выражает предельные издержки произв-ва. Величину Mf(x)=y' наз-ют мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определить пред-ую выручку, пред-ый доход, пред-ую полезность и другие пред-ые величины.

Эл-тью фун-и Ex(y) называется величина

Считаем, что y(x) эластична в точке x, если |Ex(y)|>1, y(x) неэластична, если |Ex(y)|<1, и нейтральна, если |Ex(y)|=1.

Градиент и пр-ая по напр-ию.

О. Вектор с координатами , , называется градиентом фун-и u=f(x,y,z) в т. M(x,y,z) и обозн-ся grad u = + + .

Под произв-ой фун-и u = f(x,y,z) в данном напр-ии i понимается выражение

= cosa + cosb + cosg, где cosa, cosb, cosg – направляющие косинусы вектора i(рис.).

Произв-ая предст-ет собой скорость изменения функции в данном направлении.

Теорема. Произв-я фун-и по направ-ю = проекции градиента этой фун-и на данное напр-ие (в соотв.точке).

Как известно, проекция вектора на др. вектор имеет макс. значение, если оба вектора совпадают по напр-ию.

Целевые ф-ции.

Фун-я, связ-щая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации. Целевая функция – функция, значение которой зависит от

значений эндогенных переменных. Эта функция позволяет лицу, принимающему

решения оценивать варианты.

В шир. смысле целевая функция – матем. выражение некот. критерия кач-ва одного объекта (решения, процесса и т.д.) в сравнении с другим. Примером критерия в теории статист.решений явл-ся среднеквадратический критерий точности аппроксимации(или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми). Цель – найти такие оценки, при кот. целевая фун-я достигает мин.

Важно, что критерий всегда привносится извне, и только после этого ищется правило решения, минимизирующее или максимизирующее целевую фун-ю.

Линии уровня.

- это геометр. место точек простр-ва аргументов, для кот. значения иссл. фун-и одинаковы. Это определение можно записать так:

{x ∈ E_n|F (x) = const}.

Такая запись озн-ет, что для некот. xi пространству E_n, соблюдается условие: F(x) — пост. величина.Разл. константы порождают разл. Л. у. Для случая фун-и двух переменных это можно показать на графике в виде карты Л. у. Примеры: кривые безразличия(кривая, изобр. все комбинации из двух благ, имеющих для экон. субъекта одинак. полезность и по отношению к выбору кот. он безразличен), изокванты(изолиния один. объема произв-ва продукта в завис-ти от факторов произв-ва) и изокосты(линия равных издержек.) производственной фун-и в экон-ке.

Графический метод

Осн. задача лин.о пр-ия (ОЗЛП) ставится след. образом: Имеется ряд переменных х1,х2…хn. Требуется найти такие их неотриц. значения, кот.удовл-ли бы с-ме лин.ур-ий:

{1.1}

и, кроме того, обращали бы в минимум лин. целевую фун-ю (ЦФ)

Очевидно, случай, когда ЦФ нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак фун-и и рассмотреть вместо нее фун-ю

Доп.решением ОЗЛП называют любую сов-ть пер-ных , удовл. урав-ям (1.1).

Оптим. Реш-ем наз-ют то из доп реш-й, при кот. ЦФ обращается в минимум.

На практике ограничения в ЗЛП часто заданы не уравнениями, а нер-вами. В этом случае можно перейти к ОЗЛП.

ГРАФ.МЕТОД

Теоретическое введение

Граф. метод довольно прост и нагляден для решения ЗЛП с двумя пер-ми. Он основан на геометр. представлении доп. Реш. и ЦФ задачи.

Каждое из нер-тв ЗЛП (1.2) определяет на координатной плоскости x1Ox2 некот. полуплоскость (рис.2.1), а с-ма нер-в в целом – пересечение соотв. плоскостей. Множ-во точек пересечения данных полуплоскостей наз-ся обл. доп. Реш. (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую след. Св-вом: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности с-мы ограничений задачи (1.2) ОДР является пустым множ-вом.

Вектор с координатами из коэф-тов ЦФ при и перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора C совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора C.

Суть граф. метода закл-ся в следующем:

По направлению (против направления) вектора в ОДР производится поиск оптимальной точки х*=(х₁*,х₂*). Оптимальной считается точка, через которую проходит линия уровня L_max(L_min), соотв. наибольшему (наименьшему) значению фун-и L(x). Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через кот. пройдет целевая прямая, или на всей его стороне.

При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи; существует бесконечное мн-во решений (альтернативный оптиум); ЦФ не ограничена; ОДР – единственная точка; задача не имеет решений.