13. Опред. И неопред. Интеграл, их св-ва и вз-зь. Условия интегрируемости: необх. И достаточные. Численное интегрирование.
Опред.интеграл
Опр.2.
Пусть на отрезке [a,b]
задана функция f(x).
Разобьем отрезок [a,b]
точками
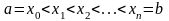на n
более мелких отрезков
,
длины которых
.
На каждом из этих отрезков выберем по
точке
.
Длину наибольшего отрезка обозначим
через
.
Определенным интегралом от функции f(x) по отрезку [a,b] называется предел интегральных сумм:
Выражение,
стоящее под знаком предела, называется
интегральной суммой для функции f(x)
по отрезку [a,b].
Числа a
и b
называются нижним и верхним пределами
интегрирования соответственно. Из
задачи о вычислении площади криволинейной
трапеции вытекает следующий геометрический
смысл определенного интеграла: если
на [a,b],
то
где S – площадь криволинейной трапеции (рис.1).
(В
дополнение) Еще существует задача
«Вычисление пути, пройденного материальной
точкой», кот. решается с пом. опред.интеграла.
Определенный
интеграл обозначается символом
Его можно найти по формуле Ньютона — Лейбница:
Пример:
Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?
(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Основные свойства определенного интеграла
1)
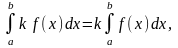k
-
постоянная.
2)
.
Эти свойства аналогичны соответствующим свойствам неопределенного интеграла.
Следующее важное свойство определенного интеграла часто используется в приложениях:
3)
где c – любая точка из (a,b).
Если функция f(x) непрерывна на отрезке [a,b], то существует такая точка c из (a,b), что
.
5) Если на [a,b], то
6)
Если
на [a,b],
то
7)
Если
на [a,b],
то
.
Неопред.интеграл
Функция F(x) называется первообразной для функции f(x), если
,
где С
– произвольная постоянная.
Опр.1 Совокупность всех первообразных для непрерывной функции f(x) называется неопределенным интегралом и обозначается
где
функция f(x)
– подынтегральная функция, f(x)dx
– подынтегральное выражение, dx
– дифференциал аргумента. Таким образом,
если F(x)
–
какая-либо
первообразная
для
f(x),
то
.
Процесс нахождения неопределенного
интеграла -интегрирование этой функции.
Пример:
Найти неопределенный интеграл.
Решение:
Из определения неопределенного интеграла вытекают следующие свойства:
5)
Благодаря формуле Ньютона-Лейбница устанавливается связь между определенным и неопределенным интегралом. А именно:
Чтобы решить определенный интеграл, надо сначала вычислить неопределенный интеграл (или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница.
Необходимое условие интегрируемости.
Теорема.Если функция интегрируема на отрезке, то она ограничена на нем.
Необх. и достат. условие интегрируемости:
Теорема. Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем необходимо и достаточно, чтобы lim∣τ∣→0(Sτ−sτ)=0 (2.1).
Это условие означает, для любого ε>0 существует δ(ε)>0, что для любого разбиения τ мелкости меньше, чем δ выполняется неравенство: ∣Sτ−sτ∣<ε (2.2). Т.к. sτ≤Sτ , то из (2.2) следует Sτ−sτ<ε .
Численное интегрирование — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
Численное интегрирование применяется, когда:
-Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.
-Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, .
В этих двух случаях невозможно вычисление интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.
Численные методы:
1) Одномерный случай
-Метод прямоугольников; Метод трапеций; Метод парабол (метод Симпсона); Увеличение точности; Метод Гаусса; Метод Гаусса-Кронрода; Метод Чебышева; Интегрирование при бесконечных пределах; Методы Монте-Карло; Методы Рунге-Кутты; Метод сплайнов
2) Многомерный случай