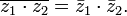7. Комплексное число
КомплЕксные
числа
(устар. Мнимые
числа),
— расширение мн-ва вещественных чисел,
обычно обозначается
.
Любое комплексное число может быть
представлено как формальная сумма
,
где
и
—
вещественные числа,
—
мнимая единица.
Комплексные
числа образуют алгебраически замкнутое
поле — это означает, что многочлен
степени
с комплексными коэффициентами имеет
ровно
комплексных корней (основная теорема
алгебры). Это одна из главных причин
широкого применения комплексных чисел
в математических исследованиях. Кроме
того, применение комплексных чисел
позволяет удобно и компактно сформулировать
многие математические модели, применяемые
в математической физике и в естественных
науках — электротехнике, гидродинамике,
картографии, квантовой механике, теории
колебаний и многих других.
Определения
Поле
комплексных чисел можно понимать как
расширение поля вещественных чисел, в
котором многочлен
имеет
корень. Следующие две элементарные
модели показывают, что непротиворечивое
построение такой системы чисел возможно.
Оба приведенных определения приводят
к изоморфным расширениям поля вещественных
чисел
,
как и любые другие конструкции поля
разложения многочлена
.
Стандартная модель
Комплексное
число
можно
определить как упорядоченную пару
вещественных чисел
.
Введём операции сложения и умножения
таких пар следующим образом:
Вещественные
числа являются в этой модели подмножеством
мн-ва комплексных чисел и представлены
парами вида
,
причём операции с такими парами
согласованы с обычными сложением и
умножением вещественных чисел. Ноль
представляется парой
единица —
а
мнимая единица —
На
множестве комплексных чисел ноль и
единица обладают теми же свойствами,
что и на множестве вещественных, а
квадрат мнимой единицы, как легко
проверить, равен
,
то есть
Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно.
Матричная модель
Комплексные числа можно также определить как семейство вещественных матриц вида
с обычным матричным сложением и умножением. Действительной единице будет соответствовать
мнимой
единице —
Действия над комплексными числами
Сравнение
означает,
что
и
(два
комплексных числа равны между собой
тогда и только тогда, когда равны их
действительные и мнимые части).
Сложение
Вычитание
Умножение
Деление
Геометрическая модель
Геометрическое представление комплексного числа
Рассмотрим
плоскость с прямоугольной системой
координат. Каждому комплексному числу
сопоставим
точку плоскости с координатами
(а
также радиус-вектор, соединяющий начало
координат с этой точкой). Такая плоскость
называется комплексной. Вещественные
числа на ней занимают горизонтальную
ось, мнимая единица изображается
единицей на вертикальной оси; по этой
причине горизонтальная и вертикальная
оси называются соответственно
вещественной
и мнимой
осями.
Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент). Подробнее см. ниже.
В этом наглядном представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».
Геометрическая модель комплексных чисел широко используется в планиметрии: многие планиметрические теоремы можно доказать как некоторые комплексные тождества. Часто этот метод даёт наиболее простое док-во.
Связанные определения
Модуль, аргумент, вещественная и мнимая части
Пусть
—
комплексное число, где
и
—
вещественные числа. Числа
или
и
или
называются
соответственно вещественной
и мнимой
(аналогично англ. real,
imaginary)
частями
.
Если
,
то
называется
мнимым
или чисто
мнимым
числом.Если
,
то
является
действительным (вещественным) числом.
Модуль и аргумент
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль
комплексного числа
обозначается
и
определяется выражением
.
Часто обозначается буквами
или
.
Если
является
вещественным числом, то
совпадает
с абсолютной величиной этого вещественного
числа.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
(сопряжённое
к сопряжённому есть исходное).
