^{1.Мн-ва и способы их задания}.Операции над мн-вами.Счетные и несчетные мн-ва.Нечеткие мн-ва и алгоритмы.

Понятие мн-ва является первоначальным матем. понятием, т.е. таким понятием: Студенты одной группы – мн-во, эл-ты кот.- студенты, общее св-во – обучение одной специальности. Мн-во В – корни уравнения ½ = cosx. Эл-ты – вещественные числа, общее св-во – обращают данное уравнение в верное равенство.

Мн-во - это сов-ть, класс отличающихся друг от друга объектов, объед-ых каким-либо общим свойством. Объекты, входящие в эту сов-ть, наз-ся элементами мн-ва.Мн-ва обозн-ся заглавными буквами лат. алфавита, а эл-ты мн-ва- строчными.

Классы (мн-ва) чисел: N – натуральные числа(целые «+» числа), Z – целые(«+ и -»целые и 0) , Q- рациональные(числа, кот. могут быть записаны в виде обыкн. дроби m/n, где m,n– целые числа), R- действительные (рац. и иррацион.числа), C – комплЕксные(мнимые числа х+iy).

Если х – элемент мн-ва Х, то говорят: хЄХ. Если х не принадлежит Х, то пишут хє/Х. Виды мн-в : конечные мн-ва, бесконечные, пустые(Ø), универсальные(U-вкл-щее в себя все объекты).Конечные и бескон. мн-ва подразделяются на неупорядоч. и упорядоч.; неупорядоч. бескон. – на счетные и несчетные.

Рассмотрим два основных способа задания неупорядоч. множеств:

1. перечисление всех его элементов;

2. описание характеристического (общего) свойства его элементов.

Первым способом задаются конечные мн-ва. Примеры:

А – мн-во чисел, являющихся делителями числа 20: А = {1, 2, 4, 5, 10, 20}.

В – список группы: В = {Архипов, Белов,…}.

Вторым способом можно задать конечные мн-ва, бесконечные, пустые. Мн-во эл-тов,Обладающих характеристическим св-вом Р, обозначается:

{x | P(x)} и читается так: мн-во всех х таких, что х обладает свойством Р(х).

Примеры: {x | x ЄR, x2 – 4 = 0} - это конечное мн-во и его можно задать перечислением элементов : {2, -2}. {x | x Є R, 2< x < 5 } – бесконечное несчетное мн-во, а именно, числовой промежуток (2, 5).

{x | x Є R, 1= sinx} – бесконечное счетное мн-во.

{x | x Є R, x2 + 9 = 0 } – это пустое мн-во, т.к. ни одно вещественное число не удовлетворяет данному уравнению.

Операции над мн-вами:

1.Объединение(сумма) мн-в А и В – это мн-во, содержащее эл-ты, принадлежащие мн-ву А или В. Обозначается АUВ = {x | xЄA или хЄ В}. Диаграмма Эйлера-Венна(заштрихованные круги):

П ример: А = {2, 5, 7, 9}, В = {3, 5, 8, 9, 12}.

АUВ = {2, 5, 7, 9}U{3, 5, 8, 9, 12}= {2, 5, 7, 9, 3, 8, 12}.

2.Пересечение(произведение) мн-в А и В - это мн-во, состоящее из эл-тов, кот. Є мн-ву А и мн-ву В.

Краткая запись: АΩВ = {x | xЄA и хЄВ}. Диаграмма Э-В:

Пример: АΩВ= {2, 5, 7, 9}Ω{3, 5, 8, 9, 12}= {5,9}.

3. Разность мн-в А и В -это мн-во, состоящее из элементов, кот. Є А и не принадлежат В.

Краткая запись: А\В = {x| xЄ A и xЄ/B}. Диаграмма Э-В:

Пример: А\В = {2, 5, 7, 9}\{3, 5, 8, 9, 12}= {2, 7}.

Если АΩВ = Ø, то А\В= А и В\А = В.

4. Симметрическая разность мн-в А и В -это мн-во, состоящее из элементов, кот.е принадлежат А\В или В\А.

Краткая запись: A∆B= {x| xЄA\B или xЄB\A}. Диаграмма Э-В.

Пример: АΔВ = {2, 5, 7, 9}Δ{3, 5, 8, 9, 12}= {2, 7, 3, 8, 12}.

Счетные и несчетные мн-ва.

Всякое мн-во, эквивалентное мн-ву натуральных чисел, называется счетным. Такое мн-во можно "пересчитать": пронумеровать все его элементы натуральными числами. Например, мн-во Q-счетно.

Док-во:

Представим мн-во всех рац- чисел в виде бесконечной таблицы.

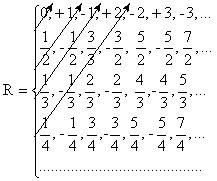
Оценим, как строятся строки этой таблицы.

1ая строка – это все целые числа, располож. по возрастанию их модуля и так, что знаки “+” и “–” чередуются.

2ая строка – это все несократимые дроби со знамен. 2, распол.по возр. их модуля и так, что знаки “+” и “–” чередуются.

3я строка – это все несократимые дроби со знамен. 3, распол. по возр. их модуля и так, что знаки “+” и “–” чередуются.

Вообще,n-ая строка это все несократимые дроби со знамен. n, распол. по возр. их модуля и так, что знаки “+” и “–” чередуются.

Очевидно, что в этой таблице находятся все рац. числа. Используя прием диагонализации представим R в виде:

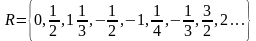
Так как R представилось в форме последовательности, то =>, что R –счетное мн-во.

Несчётное мн-во — такое бесконечное мн-во, которое не является счётным. Таким образом, любое мн-во является либо конечным, либо счётным, либо несчётным.

Примеры: Счётные мн-ва: Простые числа(делятся на 1 и самого себя), N,Z,Q, Вычислимые числа,Мн-во всех конечных слов над конечным или счётным алфавитом,Любое бесконечное семейство непересекающихся открытых интервалов на действительной оси,Мн-во всех прямых на плоскости, каждая из которых содержит хотя бы 2 точки с рациональными координатами,Любое бесконечное мн-во точек на плоскости, все попарные расстояния между элементами которого рациональны

Несчётные мн-ва: Вещественные числа,КомплЕксные числа(мнимые числа х+iy).

Разл. понятия, нечеткие по своей природе, могут быть формально описаны посредством нечетких множеств. Нечёткое мн-во А(Лотфи Заде в 1965) - это совокупность A={(x,μ_A (x))|xЄX}, где X — универс. Мн-во, а μ_A (x)— функция принадлежности (характер. функция), характеризующая степень принадлежности элемента x нечёткому множеству A. Xарактерист. функция может принимать любые значения в интервале [0,1], а не только значения 0 или 1(Как у Кантора). Теория нечётких мн-в сводится к теории вероятностей. Однако при практ. применении аппарат теории нечётких множеств обычно используется самостоятельно. Для описания сложных соотношений м-ду перем-ми удобно исп-ть нечеткие алгоритмы. Нечеткий алгоритм, упрощенно говоря, опред-ся упорядоченным мн-вом нечетких инструкций (нечетких высказываний), которые содержат понятия, формализуемые нечеткими множествами. Нечеткие инструкции-инструкции, содержащие нечеткое понятие, н-р, "пройти около 100 метров". Пример: Алгоритмы описания отношений между нечеткими переменными, н-р, в виде послед-ти нечетких инструкций типа: "если х мало и х увеличить слегка, то у увеличится слабо"; такие алгоритмы позволяют приближенно описывать поведение систем, входные и выходные сигналы. Мир алгоритмов очень разнообразен. Несмотря на это , удается выделить общие свойства, которым обладает каждый алгоритм. Внимательно анализируя примеры алгоритмов, можно найти в них много общего, несмотря на различие в сути самих действий. Эти общие характ-ки называют свойствами алгоритма. Рассмотрим их.

•Дискретность - любой алгоритм должен состоять из конкретных действий, следующих в опред. порядке. Для всех алгоритмов общим является необход-ть строго соблюдения послед-ти выполнения действий.

•Детерминированность - любое действие алгоритма должно быть строго и недвусмысленно определено в каждом случае.

•Конечность- каждое в отдельности и алгоритм в целом должны иметь возможность завершения.

•Массовость - один и тот же алгоритм можно использовать с разными исходными данными.

•Результативность - чтобы в алгоритме не было ошибок.

Описания действий в алгоритме следуют послед-но друг за другом. Однако очередность выполнения этих действий может быть изменена, если в алгоритме предусмотрен анализ некоторого условия. Путём включения условий создаются алгоритмы с различной структурой, в которой всегда можно выделить несколько типовых конструкций: лин., циклическую, разветвляющуюся и вспомогательную.

Линейный (послед-ый) алгоритм – описание действий, которые выполняются однократно в заданном порядке.Например: Требуется составить алгоритм вычисления резалта выражения:

100 + 15 – 40 + 20 1.Сложить числа 100 и 15. 2. Из полученной суммы вычесть 40. 3. К результату прибавить 20. Разветвл. алгоритм – алгоритм, в котором в завис-ти от условия выполняется либо одна, либо другая послед-ть действий.

Условие – выражение, находящееся между словом «если» и словом «то», и принимающее значение «истина» или «ложь».

В общем случае схема разветвляющего алгоритма выглядит так: «если условие, то … иначе».

Например, в предложении из сказки А.С. Пушкина о коте: «идет направо – песнь заводит, налево – сказку говорит».

Такое представление алгоритма получило название полная форма.

Неполная форма выглядит так: ««если условие, то …»

Например, в предложении «если выучишь урок, то получишь хорошую отметку!».

Цикл. алгоритм – описание действий, которые должны повторяться указанное число или пока не выполнено заданное условие.

Перечень повторяющихся действий называется телом цикла.

Вспомогательный алгоритм – алгоритм, который можно использовать в других алгоритмах, указав только его имя. Вспомогательному алгоритму должно быть присвоено имя.

Понятие вспомог. алгоритма значительно упрощает процесс алгоритмизации задачи. Создавая алгоритм, вы описываете действие резалтом которого должно быть достижение поставленной цели. Этому алгоритму можно дать уникальное имя.

Если в процессе алгоритмизации удается выделить более простые этапы и для каждого из них установить подцели, то для их достижения рекомендуется разрабатывать вспомог. алгоритмы. Итоговый алгоритм выглядит как связанные между собой вспомог. алгоритмы, представленные только своими именами, причем описания самих вспомог. алгоритмов хранятся отдельно.

2.Векторное (линейное) пространство. Пусть L – некоторое мн-во, элементы которого можно складывать и умножать на числа из F (где F – мн-во рациональных, действительных или комплексных чисел).

ОПР1. Мн-во L называется линейным пространством над F если для любых элементов a,b,cL и для любых чисел ,F выполняются условия:

1. a+b=b+a (коммутативность сложения элементов из L);

2. (a+b)+c=a+(b+c) (ассоциативность сложения элементов из L);

3. Во множестве L существует такой элемент o, что a+o=a. Элемент o называют нулевым элементом мн-ва L;

4. Для любого элемента a L  элемент –a L такой, что a+(–a)=o. Элемент –a называют противоположным к a;

5. (a)=()a (ассоциативность относительно умножения чисел);

6. (+)a=a+a (дистрибутивность умножения на элемент из L относительно сложения чисел);

7. (a+b)=a+b (дистрибутивность умножения на число относительно сложения элементов из L);

8. 1a=a.

Линейное пространство над R называют еще вещественным (действительными) линейным пространством, а над C комплексным.

ЛЕММА 2 (простейшие свойства элементов линейного пространства).

Пусть L – линейное пространство над F. Тогда для любых элементов a,b L и любых чисел , F справедливы следующие утверждения:

1) 0·a = o, ·o = o;

2) (–) · a =  ·(–a) = –a, (–) ·(–a) = a;

3)  ·(a–b) = a – b, (–) · a = a – a.

Наряду с термином «линейное пространство» используется также термин «векторное пространство», а элементы линейного пространства принято называть векторами.

Пусть L – линейное пространство над F, L₁ – непустое подмножество в L.

ОПР. Говорят, что L₁ является подпространством линейного пространства L (или линейным подпространством), если оно само образует линейное пространство относительно операций, определенных на L .Если L₁ является подпространством линейного пространства L, то пишут: L₁ ≤ L

ТЕОРЕМА 3 (критерий подпространства).

Пусть L – линейное пространство над F, L₁ – непустое подмножество в L . L₁ является подпространством линейного пространства L тогда и только тогда, когда для любых элементов a,b L₁ и любого  F выполняются условия:

1) a – b L₁;

2) ·a  L₁.

Лин. завис-ть и независимость векторов

Введенные нами линейные операции над векторами дают возможность составлять различные выражения для векторных величин и преобразовывать их при помощи установленных для этих операций свойств.

Исходя из заданного набора векторов a1, ..., an, можно составить выражение вида

где α₁, ..., α_n — произвольные действительные числа. Это выражение называют лин. комбинацией векторов a₁, ..., a_n. Числа a_i, i = 1, n, представляют собой коэффициенты лин. комбинации. Набор векторов называют еще системой векторов.

В связи с введенным понятием лин. комбинации векторов возникает задача описания мн-ва векторов, которые могут быть записаны в виде лин. комбинации данной системы векторов a1, ..., an. Кроме того, закономерны вопросы об условиях, при которых существует представление вектора в виде лин. комбинации, и о единств-ти такого представления.

Опр..Векторы a₁, ..., a_n называют линейно зависимыми, если существует такой набор К-ов α₁, ..., α_n, что

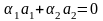
и при этом хотя бы один из этих К-ов ненулевой. Если указанного набора К-ов не существует, то векторы называют линейно независимыми.

Если α₁ = ... = α_n = 0, то, очевидно, α₁a₁ + ... + α_na_n = 0. Имея это в виду, можем сказать так: векторы a₁, ..., a_n линейно независимы, если из равенства (2.2) вытекает, что все коэффициенты α₁, ..., α_n равны нулю.

Следующая теорема поясняет, почему новое понятие названо термином "завис-ть" (или "независимость"), и дает простой критерий лин. завис-ти.

Теорема. Для того чтобы векторы a1, ..., an, n > 1, были линейно зависимы, необходимо и достаточно, чтобы один из них являлся лин. комбинацией остальных.

◄ Необходимость. Предположим, что векторы a1, ..., an линейно зависимы. Согласно определению 2.1 лин. завис-ти, в равенстве (2.2) слева есть хотя бы один ненулевой К, например α1. Оставив первое слагаемое в левой части равенства, перенесем остальные в правую часть, меняя, как обычно, у них знаки. Разделив полученное равенство на α1 , получим

т.е. представление вектора a1 в виде лин. комбинации остальных векторов a2, ..., an.

Достаточность. Пусть, например, первый вектор a₁ можно представить в виде лин. комбинации остальных векторов: a1 = β₂a₂ + ... + β_na_n. Перенеся все слагаемые из правой части в левую, получим a₁ - β₂a₂ - ... - β_na_n = 0, т.е. лин. комбинацию векторов a1, ..., an с коэффициентами α₁ = 1, α₂ = -β₂, ..., α_n = -β_n, равную нулевому вектору. В этой лин. комбинации не все коэффициенты равны нулю. Согласно определению 2.1, векторы a₁, ..., a_n линейно зависимы. ►

Определение и критерий лин. завис-ти сформулированы так, что подразумевают наличие двух или более векторов. Однако можно также говорить о лин. завис-ти одного вектора. Чтобы реализовать такую возможность, нужно вместо векторы линейно зависимы" говорить система векторов линейно зависима". Нетрудно убедиться, что выражение система из одного вектора линейно зависима" означает, что этот единственный вектор является нулевым (в лин. комбинации имеется только один К, и он не должен равняться нулю).

Понятие лин. завис-ти имеет простую геометрическую интерпретацию. Эту интерпретацию проясняют следующие три утверждения.

Теорема 2.2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

◄ Если векторы a и b линейно зависимы, то один из них, например a, выражается через другой, т.е. a = λb для некоторого действительного числа λ. Согласно определению 1.7 произведения вектора на число, векторы a и b являются коллинеарными.

Пусть теперь векторы a и b коллинеарны. Если они оба нулевые, то очевидно, что они линейно зависимы, так как любая их лин. комбинация равна нулевому вектору. Пусть один из этих векторов не равен 0, например вектор b. Обозначим через λ отношение длин векторов: λ = |a|/|b|. Коллинеарные векторы могут быть однонаправленными или противоположно направленными. В последнем случае у λ изменим знак. Тогда, проверяя определение 1.7, убеждаемся, что a = λb. Согласно теореме 2.1, векторы a и b линейно зависимы. ►

Замечание 2.1. В случае двух векторов, учитывая критерий лин. завис-ти, доказанную теорему можно переформулировать так: два вектора коллинеарны тогда и только тогда, когда один из них представляется как произведение другого на число. Это является удобным критерием коллинеарности двух векторов.

Теорема 2.3. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

◄ Если три вектора a, b, с линейно зависимы, то, согласно теореме 2.1, один из них, например a, является лин. комбинацией остальных: a = βb + γс. Совместим начала векторов b и с в точке A. Тогда векторы βb, γc будут иметь общее начало в точке A и по правилу параллелограмма их сумма, т.е. вектор a, будет представлять собой вектор с началом A и концом, являющимся вершиной параллелограмма, построенного на векторах-слагаемых. Таким образом, все векторы лежат в одной плоскости, т. е. компланарны.

Пусть векторы a, b, с компланарны. Если один из этих векторов является нулевым, то очевидно, что он будет лин. комбинацией остальных. Достаточно все коэффициенты лин. комбинации взять равными нулю. Поэтому можно считать, что все три вектора не являются нулевыми. Совместим начала этих векторов в общей точке O. Пусть их концами будут соответственно точки A, B, C (рис. 2.1). Через точку C проведем прямые, параллельные прямым, проходящим через пары точек O, A и O, B. Обозначив точки пересечения через A' и B', получим параллелограмм OA'CB', следовательно, OC = OA' + OB'. Вектор OA' и ненулевой вектор a = OA коллинеарны, а потому первый из них может быть получен умножением второго на действительное число α: OA' = αOА. Аналогично ОВ' = βOB, β ∈ R. В результате получаем, что ОС =α оА+βOB, т.е. вектор с является лин. комбинацией векторов a и b. Согласно теореме 2.1, векторы a, b, с являются линейно зависимыми. ►

Теорема 2.4. Любые четыре вектора линейно зависимы.

◄ Док-во проводим по той же схеме, что и в теореме 2.3. Рассмотрим произвольные четыре вектора a, b, с и d. Если один из четырех векторов является нулевым, либо среди них есть два коллинеарных вектора, либо три из четырех векторов компланарны, то эти четыре вектора линейно зависимы. Например, если векторы a и b коллинеарны, то мы можем составить их лин. комбинацию αa+βb = 0 с ненулевыми коэффициентами, а затем в эту комбинацию добавить оставшиеся два вектора, взяв в качестве К-ов нули. Получим равную 0 лин. комбинацию четырех векторов, в которой есть ненулевые коэффициенты.

Таким образом, мы можем считать, что среди выбранных четырех векторов нет нулевых, никакие два не коллинеарны и никакие три не являются компланарными. Выберем в качестве их общего начала точку O. Тогда концами векторов a, b, с, d будут некоторые точки A, B, C, D (рис. 2.2). Через точку D проведем три плоскости, параллельные плоскостям OBC, OCA, OAB, и пусть A', B', C' — точки пересечения этих плоскостей с прямыми OA, OB, OC соответственно. Мы получаем параллелепипед OA'C"B'C'B"DA", и векторы a, b, с лежат на его ребрах, выходящих из вершины O. Так как четырехугольник OC"DC' является параллелограммом, то OD = ОС'' + ОС''. В свою очередь, отрезок OC'' является диагональю параллелограмма OA'C"B', так что ОС" = ОА' + ОВ', а OD = OA' + OB' + OC'.

Остается заметить, что пары векторов ОА ≠ 0 и ОА', ОВ ≠ 0 и ОВ', ОС ≠ 0 и ОС' коллинеарны, и, следовательно, можно подобрать коэффициенты α, β, γ так, что OA' = αOА, ОВ' = βOB и OC' = yOC. Окончательно получаем OD = αOA + βOB + γOC. Следовательно, вектор OD выражается через остальные три вектора, а все четыре вектора, согласно теореме 2.1, линейно зависимы. ►

Базис и ранг системы векторов

Пусть задана система векторов a1, a2, ..., am (1)

Выделим из этой системы подсистему ai1, ai2, ..., air (2), где числа i1, i2, ir - какие-то из чисел от (1; m). Подсистема (2) является максимальной линейно независимой подсистемой или базисом системы (1), если векторы системы (2) линейно независимы, а любой вектор системы (1) является их лин. комбинацией.

Пр-р: e1и e2 являются базисом всех двухмерных векторов (e1 по оси 0x, а e2 по оси 0y). A= c1e1+ c2e2.

В одной и той же системе векторов может быть несколько базисов, но число векторов в каждом базисе одно и то же.

Два различных базиса одной и той же системы векторов содержит одинаковое количество векторов.

Рангом системы векторов называется число векторов в любом базисе системы, т.е. рангом системы векторов является максимальное число линейно независимых векторов системы.

Ранг «r» R2= 2. Система, состоящая более чем из n n-мерных векторов линейно зависима. Отсюда следует, что базис любой системы векторов состоит из конечного числа векторов и оно не превосходит n. Rn будет иметь максимальное число линейно независимых векторов n (размерность - n). Любой базис n-мерного векторного пространства содержит n векторов

Линейное программирование — это метод мат. моделирования, разработанный для оптимизации использования ограниченных ресурсов. ЛП успешно применяется в военной области, индустрии, сельском хозяйстве, транспортной отрасли, экономике, системе здравоохранения и даже в социальных науках. Широкое использование этого метода также подкрепляется высокоэффективными компьютерными алгоритмами, реализующими данный метод. На алгоритмах линейного программирования базируются оптимизационные алгоритмы для других, более сложных типов моделей и задач исследования операций (ИО), включая целочисленное, нелинейное и стохастическое программирование.

Оптимизационная задача – это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

В самом общем виде задача линейного программирования математически записывается следующим образом:

U=f(X) →max, X W (1)

где X = (x₁, x₂ , ... , x_n); W – область допустимых значений переменных x₁, x₂ , ... , x_n ;f(Х) – целевая функция.

Для того чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т.е. указать X₀ W такое, что f(X₀)≥f(X) при любом X W.

Оптимизац. задача является неразрешимой, если она не имеет опт. решения. В частности, задача максимизации будет неразрешимой, если целевая функция f(Х) не ограничена сверху на допустимом множестве W.

Методы решения опт.задач зависят как от вида целевой функции f(Х), так и от строения допустимого мн-ва W. Если целевая функция в задаче является функцией n переменных, то методы решения называют методами мат. программирования.

Характ. черты задач ЛП следующие:

показатель оптимальности f(X) представляет собой лин. функцию от эл-тов решения X = (x₁, x₂, ... , x_n); ограничит. условия, налагаемые на возможные решения, имеют вид лин.рав-в или неравенств.

Задачей лин. прогр-ия называется задача исслед-ия операций, мат. модель которой имеет вид: f(X)= →max(min) (2) (3)

(4)

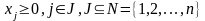(5)

При этом система лин. ур-ий (3) и нер-тв (4), (5), опред. допустимое мн-во решений задачи W, называется с-мой ограничений задачи лин. прогр-ния, а лин. функция f(Х) называется целевой функцией или критерием оптим-сти.

При описании реал. ситуации с помощью лин. модели следует проверять наличие у модели таких св-в, как пропорц-сть и аддитивность. Пропорц-сть означает, что вклад каждой переменной в целевой функции и общий объем потреб-ия соответств. ресурсов должен быть прямо пропорц-ен величине этой переменной. Например, если, продавая j-й товар в общем случае по цене 100 рублей, фирма будет делать скидку при определенном уровне закупки до уровня цены 95 рублей, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной xj. Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход. Аддитивность означает, что целевая функция и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.

Допустимое решение – это совокупность чисел (план) X = (x1, x2, ... , xn), удовлетв-их ограничениям задачи. Оптим. решение – это план, при котором цел. функция принимает свое макс. (мин.) значение.

3.Матрицы и определители. Методы вычисления определителей. Миноры и алгебраические дополнения. Теорема о разложении определителя по строке (столбцу). Применения матриц в экономических задачах (теория игр, математическое программирование).

Матрицей А размера m x n наз-ся прямоуг. таблица из m строк и n столбцов, состоящая из чисел или иных матем. выражений aij (называемых элементами матрицы), Первый индекс (i) указывает номер строки, а второй (j) –номер столбца, на пересечении кот. стоит элемент aij.

Коротко матрицу обозн-ют так: A=(aij)

Пример 1: - матрица (2х3), ее элементы a11=1, a12=x, a13=3, a21=-2y .

Размер матрицы записывается так: (m x n).

Векторы можно рассм-ть, как частные случаи матриц. Напр., n-мерная вектор-строка, является матрицей размера (1 х n), а m -мерный вектор-столбец – матрицей (m x 1).

- вектор-строка, - вектор-столбец.

Квадратной матрицей n-го порядка называется матрица, в кот. число строк = числу столбцов (m=n), размерность – (n x n).

Прямоугольной матрицей наз-ся матрица, в кот. число строк и столбцов не совпадают.

Определитель

Пусть дана квадратная матрица:

Определителем, соответствующим данной квадратной матрице А, называют число, обозначаемое символом:

Определителем второго порядка называют число

Определителем третьего порядка называют число

Чтобы запомнить, какие произведения в правой части равенства (3) берутся со знаком "+”, а какие со знаком "-”, полезно использовать следующее правило треугольников (правило Саррюса):

Методы вычисления определителей.

1). Разложение по строке или столбцу.

2). Метод обращения в нуль всех, кроме одного, эл-тов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), зануляются все эл-ты выбранной строки (столбца) кроме одного, принадлежащего вычитаемому столбцу (строке).

3). Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, исп-ется для послед.зануления всех эл-тов первой строки (столбца) кроме одного, второй строки (столбца) – всех кроме двух и т.д. В итоге определитель преобразуется к треугольному виду. Величина такого определителя = произведению элементов главной диагонали.

4). Вычисление с исп-нием теоремы Лапласа, согласно кот. определитель n- го порядка = сумме произведений всех его миноров n-го порядка, стоящих в выделенных строках (столбцах), на их алгебраические дополнения.

Минором Mij элемента aij (i,j=1,n) наз-ся определитель (n-1)-го порядка, полученный из определителя n-го порядка, вычерчиванием i-й строки и j-го столбца. Алгебраическое дополнение Aij элемента Aij определяется рав-вом

Aij=(-1)i+j Mij

Для произвольного натурального числа (теорема Лапласа, разложение по i-строке)

Для определителя III-го порядка (при i = 1): Алгебраическим дополнением данного элемента называется его минор, умноженный на (n - 1)k, где k - сумма номеров строки и столбца, содержащих данный элемент.

Т. О., знак, который при этом приписывается минору соответствующего эл-та определителя, определяется след. таблицей:

В приведенном выше рав-ве, выражающем определитель 3 порядка, в правой части стоит сумма произведений эл-тов первой строки определителя на их алгебраические дополнения.

Верна общая теорема: определитель третьего порядка =н сумме произведений эл-тов любой его строки или столбца на их алгебраические дополнения. Эта теорема позволяет вычислять значение определителя, раскрывая его по эл-там любой его строки или столбца.

Отметим, что сумма произведений эл-тов какого-либо ряда на алгебраические дополнения эл-тов другого, но параллельного исходному ряда, всегда = 0.

Важнейшие свойства определителей второго и третьего порядков:

1) Определитель не изменится, если строки определителя заменить столбцами, а столбцы - соответствующими строками.

2) Общий множитель элементов какой-нибудь строки (или столбца) может быть вынесен за знак определителя.

3) Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца) этого определителя, то определитель равен нулю.

4) При перестановке двух строк (столбцов) определителя знак этого определителя меняется на противоположный.

5) Определитель не изменится, если к элементам одной строки (столбца) определителя прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число (теорема о лин. комбинации параллельных рядов определителя).

Разложение определителя по элементам строки или столбца

Рассмотрим квадратную матрицу A n-го порядка.

Выберем i,j-ый эл-т этой матрицы и вычеркнем i-ую строку и j-ый столбец. В рез-те мы получаем матрицу (n – 1)-го порядка, определитель кот. наз-ся минором эл-та и обозн-ся символом Mi j:

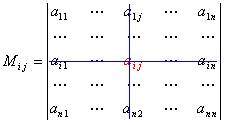
Алгебраическое дополнение Ai,j элемента ai j определяется формулой

Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:

Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:

Теоремы о разложении определителя имеют важное значение в теоретических иссл-ях. Они устанавливают, что проблема вычисления определителя n-го порядка сводится к проблеме вычисления n определителей (n –1)-го порядка.

Применение матриц в экономике(теория игр)

В нормальной, или стратегической, форме игра описывается платёжной матрицей. Каждая сторона (точнее, измерение) матрицы — это игрок, строки определяют стратегии первого игрока, а столбцы — второго. На пересечении двух стратегий можно увидеть выигрыши, которые получат игроки. В примере справа, если игрок 1 выбирает первую стратегию, а второй игрок — вторую стратегию, то на пересечении мы видим (−1, −1), это значит, что в результате хода оба игрока потеряли по одному очку.

	Игрок 2 стратегия 1	Игрок 2 стратегия 2
Игрок 1 стратегия 1	4, 3	–1, –1
Игрок 1 стратегия 2	0, 0	3, 4
Нормальная форма для игры с 2 игроками, у каждого из которых по 2 стратегии.

Игроки выбирали стратегии с макс. для себя резалтом, но проиграли, из-за незнания хода другого игрока. Обычно в нормальной форме представляются игры, в которых ходы делаются одновременно, или хотя бы полагается, что все игроки не знают о том, что делают другие участники.

(матем.програм-ие)

Матрица это не массив. Матрица в программировании это то же самое, что и в высшей математике. В программировании матрицы используются практически во всех более или менее сложных алгоритмах, таких как шифрование или хеш-функции.

В 3D графике с их помощью модифицируются координаты.

Самый простой пример реализации алгоритма с матрицами - это алгоритм решения систем уравнений – например, методом Гаусса или Крамера.

Другой вопрос, что числовые матрицы чаще всего представляют многоуровневыми массивами, это самое близкое к математической модели матриц, их реализация в языках высокого уровня.

4. Прямые на плоскости. Прямая и плоскость в пространсте., их уравнения. Взаимное расположение прямых и плоскостей.построение области допустимых решений задачи линейного программирования

Одной из простейших геометрических фигур является прямая. Алгебраическое урав-е прямой также имеет простой вид, кот. можно легко получить, пользуясь векторным методом.

Положение прямой на плоскости относительно выбранной с-мы координат вполне определяется к-либо точкой М₀ (х_0, у₀) этой прямой и ненулевым вектором n, к прямой. Вектор n наз-ся вектором нормали. На рисунке(нарисовать) изображена прямая, указанный вектор и две точки, М и М₀, принадлежащие прямой. Скалярное произведение векторов n и М₀М равно нулю, так как они взаимно ⊥. =>, обозначив через А и В коорд-ты вектора нормали, получим коорд-ое представление скалярного произведения векторов n и М₀М , т. е. ур-ие А(х–х₀)+В(у – у₀) = 0. Раскрыв скобки в этом уравнении и обозначив число (-Ах₀–Ву₀) буквой С, получим А х + В у + С = 0 Это уравнение называется общим уравнением прямой на плоскости.

Преобразовав данное уравнение, можно получить и другие способы задания прямой. Так, например, перенесем С в правую часть и разделим обе части получившегося выражения на (-С). Получим . Обозначив выражения, стоящие в знаменателе, соответственно за а и b, получим урав-е прямой в отрезках, где a и b – отрезки, отсекаемые прямой на осях OX и OY соответственно:

Любую прямую также можно задать с помощью точки, прямой и вектора, || ей (направляющий вектор). Тогда, если М₀ (х_0, у₀)-точка прямой, М (х,у) – любая другая точка этой прямой, то вектор М₀М и направляющий вектор прямой (пусть, например, это вектор р(р ₁ , р₂ ) ) будут коллинеарны(Это векторы, лежащие на одной или на || прямых). А мы знаем, что в этом случае их координаты пропорциональны, то есть можно записать 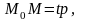подставим координаты векторов: 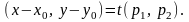Используя св-ва произведения вектора на число и рав-ва векторов, получаем два условия:

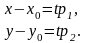Запись наз-ся параметрическими урав-ми прямой линии.

Любую прямую можно задать при помощи 2 точек. Пусть это точки М₁ (х_1, у₁) и М₂ (х_2, у₂). Точка М(х,y) – произвольная точка этой прямой. Тогда вектора М₁М₂ и М₁М будут коллинеарны.

Пространственные варианты представленных формул будут иметь похожий вид, док-во формул аналогично рассмотренному выше.

В пространстве, кроме прямой, аналитическая геометрия изучает еще один объект – плоскость. Перечислим основные способы задания плоскости. Плоскость может быть задана тремя точками М₁(x₁, y₁, z₁), M₂(x₂ y₂, z₂), M₃ (x₃, y₃, z₃). В этом случае три вектора М₁М, М₂ М₁ и M₃М₁ будут коллинеарными. А это означает, что они лежат в одной плоскости и объем параллелепипеда, построенного на этих векторах, будет равен нулю. Соответственно, будет равно нулю и их смешанное произведение, то есть

Если дана точка M ₀(x₀, y₀, z₀) и вектор, который перпендикулярен к плоскости (вектор нормали плоскости) n(A, B, C), то при составлении уравнения плоскости можно воспользоваться представлением скалярного произведения через координаты и в результате получить уравнение A(х – х₀) + B(у – у₀) + C(z – z₀) = 0. И конечно же, как и в случае прямой, определено общее уравнение плоскости, имеющее вид Ах + Ву + Сz +D = 0. И уравнение плоскости в отрезках: 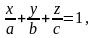где a, b, c – отрезки, отсекаемые плоскостью на осях координат.

Используя аналитическое выражение прямой и плоскости, воз­можно исследовать различные случаи взаимного расположения как двух прямых, так и прямой и плоскости, рассматривая в случае их пе­ресечения углы.

Приведем формулы, используемые при решении задач на прямую и плоскость.

Взаимное расположение плоскосте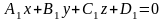й и :

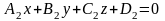а) параллельны, если При этом расстояние между параллельными прямыми вычисляется по формуле, причем коэффициенты при переменных должны быть равны. Для этого одно уравнение необходимо разделить на какое-то число или умножить.

б) совпадают, если

в) пересекаются по прямой, если ни одно из вышеприведенных равенств не выполняется.

В этом случае есть смысл говорить об угле между пересекающимися плоскостями.

Угол между плоскостями А₁x+B₁y+C₁z+D₁=0 и

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ

Пусть прямая задана точкой и направляющим вектором 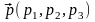, а плоскость – уравнением общего вида Ах + Ву + Сz +D = 0. Возможны следующие случаи их взаимного расположения:

а) Прямая и плоскость параллельны, если , а

б) Прямая принадлежит плоскости, если и

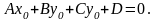
в) Прямая и плоскость пересекаются, если

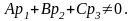
В этом случае yгол между прямой с направляющим вектором p(p₁, p₂, p₃) и плоскостью Аx+By+Cz+D=0 равен:

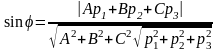
Задача линейного программирования - задача нахождения значений

параметров, обеспечивающих экстремум(макс. или мин. знач-е фун-и на заданном множ-ве) функции при наличии ограничений на аргументы. То есть, необходимо минимизировать:

 (1)

при ограничениях:

, (2)

, (3)

, (4)

где C J ( j = 1,..., n ), A IJ ( i = 1,..., m ) - заданные числа.

Задача максимизации функции (1) сводится к задаче минимизации путем замены знаков всех К-ов C J на противоположные.

Область допустимых решений – это область, в пределах которой осуществляется выбор решений (ограничения). В принципе она может быть определена разными способами, вплоть до прямого перечисления входящих в нее элементов. В экономических задачах эта область, как правило, ограничена (отсюда и происходит термин “ограничения”) условиями задачи, наличными ресурсами. Эти ограничения могут быть более жесткими и менее жесткими, соответственно область свободы — более или менее широкой. Она не существует, если определяющие ее ограничения составляют несовместную систему уравнений. В линейном программировании область допустимых решений (допустимый многогранник) всегда выпукла и всегда находится в неотрицательном подпространстве многомерного (n-мерного) пространства решений.

5. системы линейных уравнений. методы решения. разрешимость(теорема Кронекера-Капелли). Общая схема симплекс-метода.

Сист лин уравнений.Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом: ,

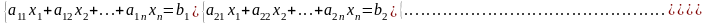где a_ij – коэффициенты, а b_i – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.Определение. Для системы линейных уравнений матрицаА = 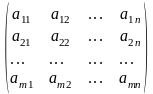называется матрицей системы, а матрица

А^*=

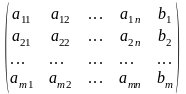
называется расширенной матрицей системы.

Определение. Если b₁, b₂, …,b_m = 0, то система называется однородной. однородная система всегда совместна, т.к. всегда имеет нулевое решение.

Теорема Крамера.Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы лин. комбинацией остальных.Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.det A  0;Действительно, если какое- либо уравнение системы есть лин. комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю. Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:x_i = _i/, где  = det A, а _i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

совпадает с ответом, полученным для данной системы методом Крамера и матричным методом. Существует другой способ решения системы лин.урав.-это метод гаусса. Это метод последовательного исключения неизвестных,он заключается в том что с помощью элементарных преобразований систем уравнений приводится к равносильной системе ступенчатого вида из кот.последовательно начиная с последних по номеру переменных находят все остальные.

Теорема Кронекера – Капелли.Система лин.урав.совместна тогда и только тогда,когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

Симплекс-Метод явл-ся универс., так как позволяет решить практически любую задачу ЛП, записанную в каноническом виде. Идея симплексного метода (метода последовательного улучшения плана) заключается в том, что начиная с некоторого исходного опорного решения осущ-ся последовательно направленное перемещение по опорным решениям задачи к оптимальному. Значение целевой функции при этом перемещении для задач на максимум не убывает. Т. к. число опорных решений конечно, то через конечное число шагов получим оптимальное опорное решение. Опорным решением называется базисное неотрицательное решение.

Алгоритм симплексного метода.

В основу симплексного метода положена идея послед. улучшения получаемого решения.

Т. о., имея с-му ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему (или, по крайней мере, не удалится от него). С новым допустимым базисным решением поступают так же, пока не отыщется решение, которое является оптимальным.

1. Математическая модель задачи должна быть канонической.

2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплексную таблицу. Все строки таблицы 1-го шага, за исключением строки Δ_j (индексная строка), заполняем по данным системы ограничений и целевой функции.

Индексная строка для переменных находится по формуле

и по формуле

Возможны следующие случаи при решении задачи на максимум:

— если все оценки Δ_j ≥ 0, то найденное решение оптимальное;

— если хотя бы одна оценка Δ_j ≤ 0, но при соответствующей переменной нет ни одного положительного К-а, решение задачи прекращаем, т.к. L()→ , т.е. целевая функция неограничена в области допусти­мых решений;

— если хотя бы одна оценка отрицательная, а при соответ­ствующей переменной есть хотя бы один положитель­ный К, то нужно перейти к другому опорно­му решению;

— если отрицательных оценок в индексной строке несколь­ко, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по аб­солютной величине отрицательная оценка.

Если хотя бы одна оценка Δ_k < 0, то k-й столбец прини­маем за ключевой. За ключевую строку принимаем ту, кото­рой соответствует минимальное отношение свободных членов (b_i) к положительным коэффициентам k-гo столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называется ключевым элементом.

3. Заполняем симплексную таблицу 2-го шага:

— переписываем ключевую строку, разделив ее на ключе­вой элемент;

— заполняем базисные столбцы;

— остальные коэффициенты таблицы находим по прави­лу "прямоугольника"(мысленно выделяется прямоугольник, в котором элемент, подлежащий пересчету и разрешающий элемент образуют одну из диагоналей). Оценки можно считать по приве­денным выше формулам или по правилу "прямоугольни­ка" Получаем новое опорное решение, которое проверяем на оптимальность, и т.д.

6. Каноническое уравнение линий 2 порядка. Уравнение в полярных координатах. Общее уравнение линии второго порядка, их канонические уравнения, фокусы, директрисы, асимптоты.

Мн-во точек,коорд.кот. удовл.урав.2степени назыв.кривой (или линией 2порядка)

Уравнение линий 2 порядка в полярных координатах. Возьмем полярную сист.коорд.с началом в фокусе рассм.прямой,а начальный луч направим через ближайшую к фокусу вершину,тогда любая лин.2порядка описывается урав.: , где ƍ – это полярный радиус, ϕ – полярный угол, P=(для эллипса и гиперболы или р – есть параметр для параболы)

Значение уравнений линий 2 порядка:

Согласно закону Кеплера все планеты двигаются по эллипсу в центре, кот.наход.солнце

Ньютон вывел что всякое тело под влиянием притяжения необходимо движется по кривой,эллипсу,параболе или ветви гиперболы.

Траектория альфа-частиц предст.собой гиперболу.

Эллипсом называется мн-во точек

п лоскости, сумма расстояний от которых до

двух данных точек F₁ и F₂ , той же плоскости,

называемых фокусами эллипса, есть величина

постоянная, большая расстояния между

фокусами. Если обозначить постоянную величину через 2а, а

расстоя­ние между фокусами через 2с и выбрать систему координат так, чтобы ось Ох проходила через фокусы, а начало координат совпадало с серединой отрезка F₁F₂ , то уравнение эллипса имеет вид

, где b²=a²-c² (a>c), которое называют каноническим уравнением эллипса. a,b,c – параметры эллипса. В этом случае фокусы эллипса F₁ (-c,0), F₂ (с,0).

Начало координат О является центром симметрии эллипса, а оси координат – осями симметрии эллипса. Точки А₁ (-а, 0), А₂ (а, 0), В₁ (0,- b), B₂ (0, b) называются вершинами эллипса, а длины отрезков а=ОА₂ и b=OB₂ – соответственно большой и малой полуосями. Ве­личина =с/а1 называется эксцентриситетом эллипса. Эксцентриси­тет характеризует вытянутость эллипса. =с/а=(а²-b²)/а=(1-b²/а²) Окружность можно считать частным случаем эллипса, у кото­рого а=b, т.е. =0. Уравнение эллипса с осями симметрии, параллель­ными координатным осям, имеет вид 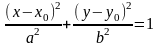, где х₀, у₀ – координаты центра симметрии эллипса.

Две прямые, перпендикулярные к большой оси эллипса и рас­положенные симметрично относительно центра на расстоянии а/ от него, называются директрисами эллипса. Если эллипс имеет уравне­ние , то уравнения директрис имеют вид х= -а/ и х= а/.

Справедлива теорема. Если r – расстояние от произвольной точки эллипса до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса. Касательной к линии второго порядка в точке М₀ называется прямая, имеющая с линией одну общую точку. В каждой точке М₀(х₀,у₀) эллипса имеется касательная, задаваемая уравнением ( хх₀)/а² + (уу₀)/b² =1.

Гиперболой называется мн-во точек

п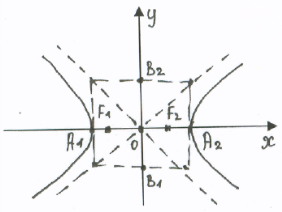 лоскости, модуль разности расстояний от

которых до двух данных точек F₁ и F₂ той же

плоскости, называемых фокусами гиперболы,

есть величина постоянная, не равная нулю и

меньшая, чем расстояние между фокусами. Если обозначить постоян­ную величину через 2а, а расстояние между фокусами через 2с и вы­брать систему координат так же, как и для эллипса, то уравнение ги­перболы примет канонический вид: 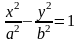, где b²=c²-а², (с>а), a,b,c – параметры эллипса.

В этом случае фокусы гиперболы F₁ (-c,0) и F₂ (с,0). Оси коор­динат являются осями симметрии гиперболы, а точка О – ее центром симметрии. Гипербола пересекает ось абсцисс в точках А₁ (-а,0) и А₂ (а,0), которые называются действительными вершинами, а величина а=ОА₂ – действительной полуосью гиперболы. Точки В₁ (0,-b), В₂ (0,b) называются мнимыми вершинами гиперболы, а величина b=ОВ₂ мнимой полуосью. Прямоугольник с центром в начале координат и сторонами, параллельными координатным осям и проходящими через вершины гиперболы, называется основным прямоугольником гипер­болы. Гипербола имеет две асимптоты, уравнения которых у=±(b/а)х. Асимптотой линии  называется такая прямая l, расстояние до которой от точки М стремится к нулю, когда точка М стремится по кривой  в бесконечность. Эксцентриситет гиперболы =с/а>1. Он характери­зует вытянутость основного прямоугольника гиперболы. =с/а=а²+b²/а=1+b²/а².Уравнение гиперболы с осями симметрии параллельными коор­динатным осям, имеет вид , где хо, уо – коор­динаты центра симметрии гиперболы. Если оси гиперболы равны, т.е. а=b, гипербола называется рав­носторонней. Ее уравнение имеет вид х²–у² =а². Для равносторонней гиперболы основной прямоугольник превращается в квадрат, а экс­центриситет равен 2. Две прямые, перпендикулярные к действительной оси гипер­болы и расположенные симметрично относительно центра на расстоя­нии а/ от него, называются директрисами гиперболы. Их уравнения имеют вид х= -а/ и х= а/ для гиперболы, заданной уравне­нием. .

Справедлива теорема: Если r – расстояние от произвольной точки гиперболы до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету гиперболы. В каждой точке М₀ ( х₀, у₀) гиперболы имеется касательная, за­даваемая уравнением ( хх₀)/а² - (уу₀)/b² =1.

Параболой называется мн-во точек

плоскости, равноудаленных от данной точки F,

той же плоскости, называемой фокусом

параболы, и данной прямой D₁D₂, лежащей

в плоскости, называемой ее директрисой и

не проходящей через фокус. Если выбрать прямоугольную систему координат так, чтобы ось Ох проходила через фокус F (F – на положи­тельном направлении ОХ) и была перпендикулярна к директрисе D₁D₂, начало которой расположить посередине между фокусом и ди­ректрисой, то уравнение параболы в этой системе координат примет канонический вид у²=2рх, где р – расстояние от фокуса до дирек­трисы. Его называют фокальным параметром параболы. Уравнение директрисы х=-р/2, фокус F( р/2,0). Начало координат является вер­шиной параболы, а ось абсцисс – ее осью симметрии. Эксцентриситет параболы =1. Если осью симметрии параболы служит ось ординат и вершина совпадает с началом координат, то уравнение параболы имеет вид х²=2ру (р>0). Уравнение директрисы в этом случае у= -р/2, фокус F (0,р/2). Уравнение параболы с осью симметрии, параллельной одной из координатных осей, имеет вид: (у-у₀)² = 2р (х-х₀) или (х-х₀)² = 2р (у-у₀ ), где х₀, у₀ – координаты вершины параболы. В ка­ждой точке М₀ ( х₀, у₀) параболы у²=2рх имеется касательная, зада­ваемая уравнением уу₀=р(х+х₀).

Уравнения эллипса, гиперболы и параболы в полярных коорди­натах, если полюс находится в фокусе, имеют одинаковый вид: r = p/ (1 -  cos). Это уравнение будет определять эллипс, если  < 1, пара­болу – при  = 1, гиперболу, когда  > 1. В этом уравнении для эл­липса и гиперболы фокальный параметр р связан с параметрами а и b формулой р = b²/a.

Общее уравнение линии второго порядка имеет вид: а₁₁х² + 2а₁₂ху + +а₂₂ у² + 2а₁₀ х + 2а₂₀ у + а₀₀ = 0 , где а₁₁² +а₁₂²+а₂₂² 0 и являются любыми действительными числами. Для того, чтобы при­вести общее уравнение линии второго порядка к каноническому (т.е. к простейшему), надо перейти к новой системе координат посредством поворота осей системы на определенный угол и переноса начала в нужную точку. Поворот осей исходной системы координат необходим лишь при а₁₂0 и реализуется на такой угол, чтобы уравнение линии в новой системе координат не содержало произведения разнородных переменных. Такая система координат всегда существует, а направле­ния осей этой системы называются главными направлениями линии второго порядка.