8. Числовые последовательности и ряды.
Числовая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Пусть
мн-во
—
это либо мн-во вещественных чисел
,
либо мн-во комплексных чисел
.
Тогда последовательность
элементов
мн-ва
называется
числовой
последовательностью.
Примеры
Функция
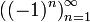является
бесконечной последовательностью целых
чисел. Начальные отрезки этой
последовательности имеют вид
.Функция
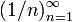является
бесконечной последовательностью
рациональных чисел. Начальные отрезки
этой последовательности имеют вид
.Функция, сопоставляющая каждому натуральному числу
одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида
.
В частности, пятым членом
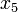этой
последовательности является слово
«май».
Суммой
числовых последовательностей
и
называется
числовая последовательность
такая,
что
.
Разностью
числовых последовательностей
и
называется
числовая последовательность
такая,
что
.
Произведением
числовых последовательностей
и
называется
числовая последовательность
такая,
что
.
Частным
числовой последовательности
и
числовой последовательности
,
все элементы которой отличны от нуля,
называется числовая последовательность
.
Если в последовательности
на позиции
всё
же имеется нулевой элемент, то резалт
деления на такую последовательность
всё равно может быть определён, как
последовательность
.
Числовые ряды.
О1: Числовым рядом называется выражение
,
где
числа
,
называемые членами ряда, образуют
известную числовую последовательность.
Например,
О2:
Числовой ряд
называется
сходящимся,
если последовательность частичных
сумм этого ряда:
конечна.
Суммой числового ряда в этом случае называется предел
Если предел не существует либо бесконечен, то ряд расходится.
Теорема 1: Необходимое условие сходимости ряда.
Если
ряд
сходится,
то
(при
).
Обратное
утверждение неверно, у ряда
общий
член
,
но ряд расходится.
Простейшие свойства числовых рядов.
1. Линейность.
Знакоположительные числовые ряды.
Теорема 2: Критерий сходимости знакоположительных рядов.
Теорема 7: Интегральный признак Коши.
Пусть
определена
на
,
непрерывна там и является невозрастающей.
Тогда ряд
сходится
сходится
интеграл
.
Пример.
Исследование ряда Дирихле
.
монотонно
убывает, непрерывна.
сходится
при
и
расходится при
.
Следовательно: {tex}\sum_{n=1}^{\infty}\frac{1}{n^{\alpha }} сходится при и расходится при .
Оценить частичные сумма ряда можно следующим способом (следует из док-ва теоремы об интегральном признаке Коши):
.
Знакопеременные и знакочередующиеся ряды.
Рассмотрим ещё два интересных частных случая числовых рядов - это знакопеременные и знакочередующиеся ряды.
Определение 3. Ряд называется знакочередующимся, если он имеет вид:
(или
), где
.
Ряды,
не являющиеся знакопостоянными (
или
)
называются знакопеременными.
ряд, - знакопеременный ряд.
Признак Даламбера и оба признака Коши в случае знакопеременных и знакочередующихся рядов не работают!
Определение 4. Ряд называется абсолютно сходящимся, если сходится.
Определение 5. Ряд называется условно сходящимся, если он сходится, но не является абсолютно сходящимся.
Теорема 8: Абсолютно сходящийся ряд сходится.
Теорема9: Признак Лейбница.