7. Моменты двумерного случайного вектора. Коэффициент корреляции

 

     При наличии двух случайных величин X и Y важно знать влияние одной на другую.  Например,  X-объем памяти, занимаемый программой из пакета прикладных программ, Y-время счёта по программе. Каждой конкретной программе из пакета соответствует точка на плоскости (x,y).

Существует определённая зависимость   от X  , которая называется регрессией Y по X.

Наиболее часто рассматривают только линейную регрессию

   (x)=ax+b ,

где коэффициенты  a и b выбираются так, чтобы получить наибольшую концентрацию точек (х,у) вблизи прямой регрессии  (x). Для их нахождения используют моменты случайного вектора (х,у).

 

Определение 7.1.

 Начальным моментом порядка  k+s случайного вектора (X,Y) называют математическое ожидание произведения , т.е.

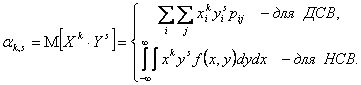
В частности:

 

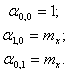
Точка с координатами    - центр распределения (рассеивания)

Определение  7.2

Центральным моментом порядка k+s называют математическое ожидание произведения  , т.е.

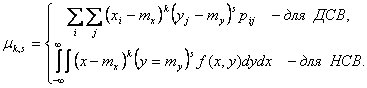
или

 

В частности  ,    .

Второй смешанный центральный момент   ввиду своей важности получил специальное название: коэффициент ковариации (или корреляционный момент) и обозначение

или 

cov(X,Y)=

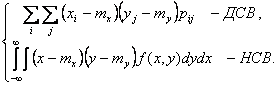
Физический смысл   - степень зависимости между X и Y.

 

Теорема 7.1 .

 Если X и Y независимые случайные величины, то их корреляционный момент равен нулю.

Доказательство.

Так как X и Y независимы, то f(x,y)=f(x)f(y) и

,

т.е. независимые случайные величины некоррелированы (несвязаны). Обратное верно не всегда. Условие некоррелированности – необходимое, но не достаточное условие их независимости, т.к.   характеризует только линейную зависимость.

     Корреляционный момент   характеризует не только зависимость X и Y, но и разброс их от своих математических ожиданий. Поэтому для характеристики взаимосвязи между случайными величинами X и Y в чистом виде (без влияния разброса) вводится понятие коэффициента корреляции (нормированной ковариации):

, .

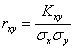
При   =0 , X и Y некоррелированы.

Приведём без доказательства, что

        или       .

Коэффициент корреляции  характеризует не всякую, а только линейную зависимость случайных величин X и Y, т.е. при наличии некоторых нелинейных зависимостей он может равняться нулю.

Значение корреляционного момента   позволяет обобщить теоремы 3 и 6 для МО и дисперсии.

 

Теорема 7.2

Математическое ожидание произведения двух случайных величин равно произведению их МО плюс их корреляционный момент.

.

Доказательство.

 

Теорема 7.2

Дисперсия суммы случайных величин равна сумме их дисперсии и удвоенного корреляционного момента:

.

Доказательство.

D[XY]=M[((x+y) –M[x+y])²] = M[((X- +(Y- ²] =

Следствие  

8. Предельные теоремы теории вероятностей.

Предельными теоремами теории вероятностей называются теоремы, устанавливающие сходимость по вероятности различных последовательностей случайных величин или функций, характеризующих распределение случайных величин, к неслучайным величинам или функциям.

Предельные теоремы разделяются на две группы. Первую группу составляют теоремы, объединённые названием «закон больших чисел», вторую – «центральные предельные теоремы».