4. Теоремы о математическом ожидании и дисперсии.

Доказательство проводится на примере дискретной случайной величины, для непрерывной случайной величины оно аналогично.

Теорема 4.1. Математическое ожидание постоянной (неслучайной, т.е. детерминированной величины) равно этой постоянной.

M[C]=C

Доказательство

Постоянную С можно рассматривать как ДСВ, которая может принимать только одно значение С с вероятностью р=1, поэтому

Теорема 4.2. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий.

Пусть X,Y – ДСВ или X,Y – НСВ.

M[X+Y]=M[X]+M[Y]

Доказательство

Рассмотрим случай, когда X и Y – ДСВ.

Пусть x₁, x₂,…,x_n,… - возможные значения СВ Х, и

p₁, p₂,…,p_n,… - их вероятности;

y₁, y₂,…,y_k,… - возможные значения СВ Y и

q₁, q₂,…,q_k,… - вероятности этих значений.

Обозначим через p_nk вероятность того, что СВ Х примет значение x_n, а СВ Y – значение y_k.

Возможные значения величины X+Y имеют вид x_n+y_n (k,n=1,2,…)

По определению математического ожидания имеем:

;

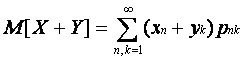Разделим эту сумму на составляющие:

.

Так как по теореме о полной вероятности

и ,

то и ,

следовательно М[X+Y]=M[X]+M[Y].

Теорема 4.3. Математическое ожидание произведения независимых случайных величин X и Y равно произведению их математических ожиданий.

Доказательство

Если X и Y – дискретные случайные величины и

x₁, x₂,…,x_n,… - возможные значения СВ Х,

p₁, p₂,…,p_n,… - вероятности этих значений;

y₁, y₂,…,y_k,… - возможные значения СВ Y и

q₁, q₂,…,q_k,… - вероятности этих значений.

то вероятность того, что СВ Х примет значение х_n, а Y – y_k равна p_nk. По определению математическое ожидание:

Следствие.

Постоянный множитель можно выносить за знак математического ожидания:

Теорема 4.4.

Математическое ожидание линейной функции случайной величины есть линейная функция математических ожиданий компонентов:

.

Доказательство.

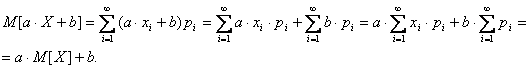
Теорема 4.5. Дисперсия детерминированной (неслучайной) величины равна нулю:

D[C]=0.

Доказательство

Или же , рассматриваем как ДСВ, которая принимает одно значение С с вероятностью 1.

Теорема 4.6.

Дисперсия суммы независимых случайных величин Х и Y равняется сумме дисперсий:

D[X+Y]=D[X]+D[Y].

Дисперсией СВ Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания:

.

Доказательство

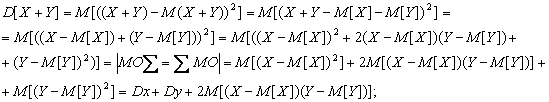
т.к. СВ Х и Y независимы, то независимы и величины (Х-М[X]) и (Y-M[Y]), следовательно:

т.к. имеем:

Следовательно, имеем .

Следствие 1.

Если Х₁, Х₂,…,Х_n - случайные величины, каждая из которых независима от суммы предыдущих, то D[X₁+X₂+…+X_n]=D[X₁]+D[X₂]+…+D[X_n]

Следствие 2.

Дисперсия сумма конечного числа попарно независимых случайных величин Х₁, Х₂,…, Х_n равна сумме их дисперсий:

Теорема 6.7. Постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

, где С=const.

Доказательство

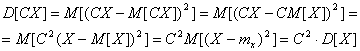
Следствие.

.

Теорема 6.8. Если Х и Y независимы, то

.

Доказательство

Основано на использовании соотношения

D[XY]=M[ (XY- M[XY])²] = M[ (XY - m_xm_y)²] = M[X²Y²]- 2M[XYm_xm_y]+M[m_x²m_y²] = M[x²]M[Y²] – 2m_xm_Y m_xm_Y+ m_x²m_Y² = M[x²]M[Y²] - m_x²m_Y²

D_x= M[x²] – m_x² -> M[x²] = D_x + m_x²

Имеем

D[XY]= M[x²] M[Y²] - m_x²m_Y² = (D_x + m_x²)( D_y + m_y²) - m_x²m_Y² =D_xD_y+D_xm_y²+ D_ym_x²+ m_x² m_y² - m_x² m_y² = D_xD_y+D_xm_y²+ D_ym_x²

Важную роль в приложении играет нормированная случайная величина.

Для нее и .