8.5. Центральные предельные теоремы

Центральные предельные теоремы доказывают, что закон распределения суммы неограниченного числа случайных величин с любыми законами распределения неограниченно приближается к нормальному. Центральные предельные теоремы – это теоремы, формулирующие условия возникновения норм закона распределения СВ.

 

Центральная предельная теорема.

Как и закон больших чисел, она имеет ряд форм. Во всех формах закона больших чисел устанавливается факт сходимости по вероятности каких-то СВ к постоянным, не случайным – при увеличении n-числа опытов или числа наблюдаемых СВ.

Другая группа предельных теорем определяет условия возникновения нор­мального распределения (закона Гаусса).

Центральная предельная теорема в различных её формах устанавливает условия, при которых возникает нормальное распределение и нарушение которых ведёт к распределению, отличному  от нормального.

Различные формы центральной предельной теоремы различаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых . Чем жёстче эти условия, тем легче доказы­вается теорема; чем они шире, тем труднее доказательство.

 Центральная предельная теорема для одинаково распределённых слагае­мых.

Если   - одинаково распределённые независимые случайные величины, с математическое ожидание   и дисперсией  , то их сумма  

при достаточно большом n имеет приближенно нормальное распределение с параметрами   и 

 Теорема Ляпунова

Пусть  - независимые случайные величины с мат. ожиданиями   и дисперсиями  , причём  при   выполняется ограничение:

,

где 

 А.М. Ляпунов показал, что при n→∞ закон распределения СВ  (2) неограни­чено приближается к нормальному. Смысл условия состоит в том, чтобы в сумме (2) не было слагаемых, влияние которых на рассеивание суммы подавляюще ве­лико по сравнению с влиянием всех остальных, а также не должно быть большого числа случай­ных слагаемых, влияние которых на рассеивание суммы исчезающе мало по сравнению с суммарным влиянием остальных.

  Ограничение может быть записано в следующем виде:

 

где   ,

А.М. Ляпунов показал, что СВ   при достаточно большом n имеет приближенно нормальное распределение с параметрами:

.

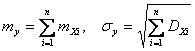Смысл ограничения (8.2) в том, чтобы случайные величины были сравнимы по порядку своего влияния на рассеивание суммы.

 

Теорема Лапласа.

Исторически первой доказанной формой центральной предельной теоремы явилась теорема Лапласа, состоящая в следующем.

Если производится n независимых опытов, в каждом из которых события А появля­ется  с вероятностью p, то при больших  n справедливо приближённое равенство:

,

где  - число появления события А в n опытах,  q=1-p;

Ф(х)- функция  Лапласа:

.

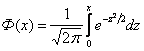Или же теорема Лапласа формулируется следующим образом. Если производится n независимых опытов, в каждом из которых со­бытие А имеет вероятность p, то при n→∞ закон распределения СВ X приближается к нормальному закону с параметрами: 

m=np,       (q=1-p).

На основе этого  можно вычислить вероятность попадания величины X не любой уча­сток   при достаточно большом n:

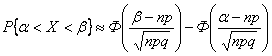   (8.5) ,

где Ф(х) – функция Лапласа.

Эта формула называется интегральной формулой Муавра-Лап­ласа (или же используется функция Лапласа  ,  ).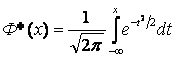

Формула Муавра-Лапласа применяется в тех случаях, когда q и p не малы:

.

 Вместо формулы (8.5) часто пользуются выражением для вероятности попадания на участок не самой СВ X, а нормированной величины:

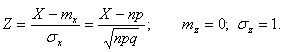
При достаточно большом n 

    при npq>>1

 

Локальная предельная теорема Муавра – Лапласа.

Теорема Лапласа дает возможность приближенно находить вероятности значений СВ, распределённых по биномиальному закону при больших значениях параметра n. При этом вероятность p не должна быть ни слишком большой, ни слишком малой.

Вероятность m успехов в n независимых испытаниях   при­ближенно можно найти с помощью локальной формулы Муавра – Лапласа:

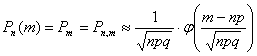     при  n→∞ , где  

 

Формула применима  при   .     Т.е. биномиальное распределение стремиться к нормальному с параметрами a=np и  .

Практически можно судить о возможности замены биномиального распределения нормальным по тому, выполнены ли при данных n и p условия: 

  ;  

.

Если эти условия соблюдены, то можно вычислять вероятности

,

где F(x) - функция распределения нормального закона,

как приращение нормальной функции распределения на участке от m до m+1.

Через функцию Лапласа функцию   можно выразить следующим образом:

,  (8.6)

где  .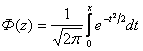

 Подставляя в формулу (8.6) значения m=np и  , получим

.

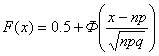Вычисляя приращения этой функции на участке от m до m+1, получим:

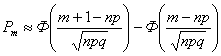        , если   .