
8.Дифференциальное уравнение электромагнитных волн.
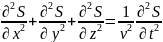 (1.1)
(1.1)
Из
уравнения Максвелла, которое описывает
электромагнитную волну
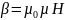 и
и
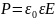
Путем преобразвания уравнений были получены уравнения
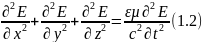
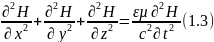
Это типичные волновые уравнения.
 V=
V=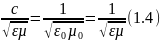
 C=
C=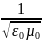 (1.5),
получим
(1.5),
получим
Если ε=1 и µ=1(вакуум), то v=с и v- скорость распростронения волны в веществе.
Из уравнения Максвелла 1.2 и 1.3 вытекают 2 следствия:
1)Поперечность электромагнитных волн, вектора В и Н взаимно перпендикулярны и перпендикулярны к распростронению волны.
2)Вектора Е и Н колеблются в одинаковых фазах, они одновременно возрастают достигают max, спадают и образ. в Ø. Причем вектора Е и Н связанны соотношением
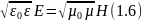
Решение
уравнений 1.2 и 1.3 является функция,
описывающая волну. В частности для
плоской монохроматической электромагнитной
волны
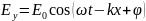
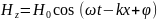 (1.7)
(1.7)
53.Собственная электропроводимость полупроводников
Полупроводники-вещества, электропроводность которых при комнатной температуре имеет промежуточное значение между электропроводностью металлов (106 — 104 Ом-1 см-1) и диэлектриков (10-8 — 10-12 Ом-1 см-1), обусловлена переносом электронов и возрастает при повышении температуры. Наиболее существенная особенность полупроводников — способность изменять свои свойства в чрезвычайно широких пределах под влиянием различных воздействий (температуры, освещения, электрического и магнитного поля, внешнего гидростатического давления). В результате таких воздействий характеристики полупроводника могут сильно изменяться, (например, электропроводность может меняться в 106-107 раз).
Собственными полупроводниками являются химически чистые полупроводники, а их проводимость называется собственной проводимостью. Примером собственных полупроводников могут служить химически чистые Ge, Se, а также многие химические соединения: InSb, GaAs, CdS и др.
Собственная проводимость возникает в результате перехода электронов с верхних уровней валентной зоны в зону проводимости. При этом в зоне проводимости появляется некоторое число носителей тока- электронов, занимающих уровни вблизи дна зоны;одновременно в валентной зоне освобождается такое же число мест на верхних уровнях, в результате чего появляются дырки.
Распределение
электронов по уровням валентной зоны
и зоны проводимости описывается функцией
Ферми-Дирака.
График функции
распределения: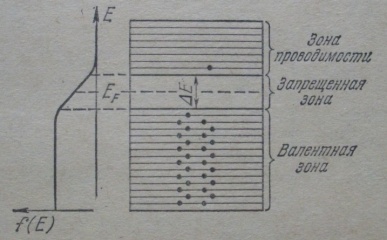
У собственных полупроводников отсчитанное от потолка валентной зоны значение уровня Ферми равно
 где,
где,
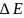 -
ширина запрещенной зоны, а
-
ширина запрещенной зоны, а
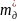 и
и
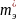 - эффективные массы дырки и электрона,
находящегося в зоне проводимости.
- эффективные массы дырки и электрона,
находящегося в зоне проводимости.
Электропроводимость собственных полупроводников быстро растет с температурой, изменяясь по закону
Ϭ=
Ϭ0exp(-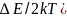 /
/
Итак, в собственном полупроводнике идут одновременно 2 процесса: рождение попарно свободных электронов и дырок и рекомбинация, приводящая к попарному исчезновению электронов и дырок. Вероятность первого процесса растет температурой. Вероятность рекомбинации пропорциональна как числу свободных электронов, так и числу дырок.
Когда внешнее электрическое поле отсутствует, электроны проводимости и дырки движутся хаотически. При включении поля на хаотическое движение накладывается упорядоченное движение: электронов против поля и дырок – в направлении поля. Оба движения- и дырок, и электронов-приводят к переносу заряда вдоль кристалла. Следовательно, собственная электропроводимость обуславливается как бы носителями заряда двух знаков-отрицательными электронами и положительными дырками.
