
- •Частные производные
- •Полное приращение и полный дифференциал
- •Частные производные высших порядков
- •Доказательство
- •5) Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •6) Производная сложной функции
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Неинвариантность дифференциалов высшего порядка
- •Дополнения
- •Решение
- •Описание метода
- •Обоснование
- •Двумерный случай
- •Двойной интеграл обозначается
- •4. Некоторые свойства двойного интеграла.
- •5. Вычисление двойного интеграла. Пусть область
- •15) Основные свойства двойного интеграла
- •17) Двойной интеграл в полярных координатах
- •19) Понятие о числовом ряде
- •Свойства сходящихся рядов
- •Доказательство
- •23) Признак Даламбера
- •Обобщенный гармонический ряд
- •Сумма ряда
- •30) Функциональные ряды
- •Степенные ряды
- •32. Интервал и радиус сходимости
- •33. Свойства степенных рядов
- •35. Разложение некоторых элементарных функций в ряд Маклорена
- •36. Приближенные вычисления значений функций с помощью степенных рядов
Решение
1. Найдём стационарные точки, решая систему (1.41):
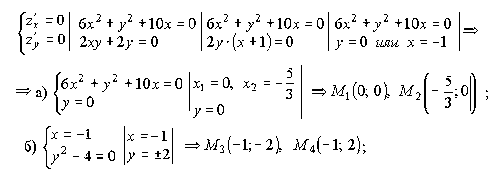
то есть найдены четыре стационарные точки. 2.
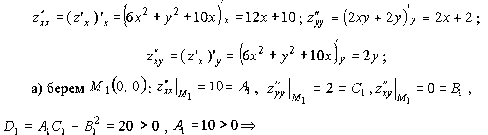
по
теореме 1.4 в точке ![]() –
минимум.
Причём
–
минимум.
Причём
![]()
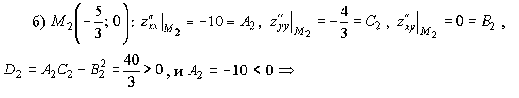
по теореме 1.4 в точке
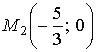
- максимум. Причём
![]()
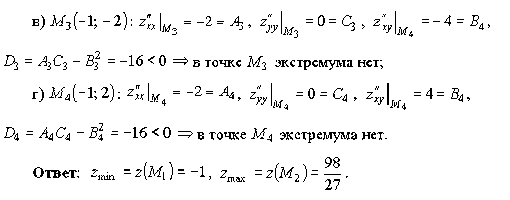
10) Во многих задачах на отыскание экстремума функции вопрос сводится к нахождению экстремума функции от нескольких переменных, которые не являются независимыми, а связаны друг с другом какими-то добавочными условиями, которые можно записать в виде уравнений, называемых уравнениями связи.
Рассмотрим, например, такую задачу: из данного куска жести площадью 2а квадратных единиц (кв. ед.) надо сделать закрытуюкоробку в форме параллелепипеда, имеющую наибольший объём.
О бозначим
линейные размеры коробки через х, у, z .
Задача сводится к отысканию максимума
функции v = хуz при
условии, что 2ху + 2хz + 2уz = 2а.
Полная поверхность параллелепипеда
равна площади куска жести. Здесь мы
имеем задачу
на условный экстремум: переменные х, у, z связаны условием 2ху + 2хz + 2уz = 2а.
Ниже мы рассмотрим метод решения подобных
задач. Ограничимся задачей об условном
экстремуме функции двух переменных,
если эти переменные связаны
только одним условием.
бозначим
линейные размеры коробки через х, у, z .
Задача сводится к отысканию максимума
функции v = хуz при
условии, что 2ху + 2хz + 2уz = 2а.
Полная поверхность параллелепипеда
равна площади куска жести. Здесь мы
имеем задачу
на условный экстремум: переменные х, у, z связаны условием 2ху + 2хz + 2уz = 2а.
Ниже мы рассмотрим метод решения подобных
задач. Ограничимся задачей об условном
экстремуме функции двух переменных,
если эти переменные связаны
только одним условием.
Определение. Условным
экстремумом функции z = f (х, у) называется
экстремум этой функции, достигнутый
при условии, что переменные х и у
связаны уравнением ![]() (х, у) = 0
(уравнением
связи).
(х, у) = 0
(уравнением
связи).
Пусть требуется найти максимумы и минимумы функции f (х, у) при условии, что х и у связаны уравнением (х, у) = 0.
При наличии условия (х, у) = 0 из двух переменных х и у независимой будет только одна, например, х, так как у определяется из равенства (х, у) = 0 как функция от х.
Найдём
полные производные ![]() и
и ![]() (см. тему
№ 14
):
(см. тему
№ 14
):
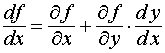 ,
(1)
,
(1)
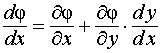 .
(2)
.
(2)
В
точках экстремума 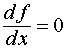 ,
то есть
,
то есть 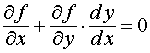 .
(3)
.
(3)
также равна нулю, так как (х, у) = 0, то есть
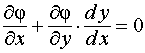 .
(4)
.
(4)
Составим
линейную комбинацию: 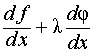 .
Получим:
.
Получим:
 или
или
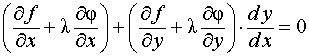 (5)
(5)
![]() –
неопределённыё
постоянный множитель.
–
неопределённыё
постоянный множитель.
Последнее равенство выполняется во всех точках экстремума. Подберём так, чтобы для значений х и у, соответствующи экстремуму функции f (х, у),, вторая скобка в равенстве (5) обратилась в нуль (метод Лагранжа).
Для определённости
будем предполагать, что в критических
точках 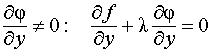 .
.
Тогда из (5) следует
равенство 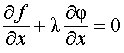 .
.
Таким образом, для отыскания экстремума получим следующую систему уравнений с тремя неизвестными х, у, :
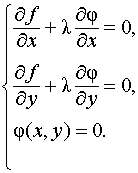 (6)
(6)
Из этих уравнений определяем х, у и коэффициент , который играет только вспомогательную роль и в дальнейшем не потребуется.
Таким образом, уравнения (6) являются необходимыми условиями условного экстремума.
Замечание. В сущности, исследование на условный экстремум функции z = f (х, у), при условии (х, у) = 0 сводится к исследованию на обычный экстремум так называемой функции Лагранжа.
u = f (х, у) + (х, у), (7)
где – неопределённый постоянный множитель.
Необходимые
условия для неё:
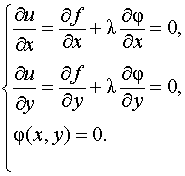 (8)
(8)
Сравните с системой (6).
Сформулируем (без вывода) достаточное условие условного экстремума в критической точке M0(x0,y0), предполагая, что функции z = f (х, у) и (х, у) = 0 имеют в точке M0 непрерывные частные производные второго порядка.
Составим функцию Лагранжа u = f (х, у) + (х, у) и определитель:
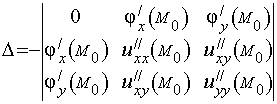 .
.
Если
определитель![]() ,
то M0 есть
точка условного минимума, если
,
то M0 есть
точка условного минимума, если ![]() ,
то M0 –
точка условного максимума.
,
то M0 –
точка условного максимума.
Пример18. Найти экстремумы функции z = x2 – y2 при условии 2x – y = 3.
Решение. Составим систему (6), считая (x, y) = 2x – y – 3:.
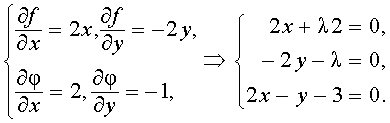
Исключая из первых двух уравнений, получим:
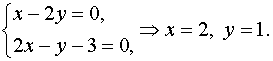
Проверим
достаточное условие. Вычислим ![]() :
:
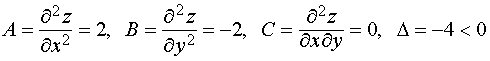
Значит, точка (2, 1) не является экстремальной для функции z = x2 – y2, но является точкой условного экстремума (условный максимум) функции z = x2 – y2 при условии 2x - y = 3: zmax = 3.
Метод
множителей Лагранжа,
метод нахождения условного
экстремума функции ![]() ,
где
,
где ![]() ,
относительно
,
относительно ![]() ограничений
ограничений ![]() ,
где
,
где ![]() меняется
от единицы до
.
меняется
от единицы до
.
