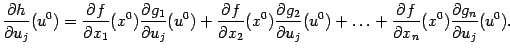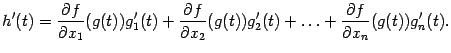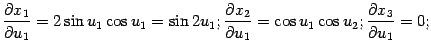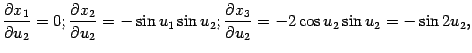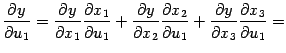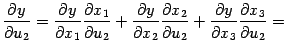- •Частные производные
- •Полное приращение и полный дифференциал
- •Частные производные высших порядков
- •Доказательство
- •5) Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •6) Производная сложной функции
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Неинвариантность дифференциалов высшего порядка
- •Дополнения
- •Решение
- •Описание метода
- •Обоснование
- •Двумерный случай
- •Двойной интеграл обозначается
- •4. Некоторые свойства двойного интеграла.
- •5. Вычисление двойного интеграла. Пусть область
- •15) Основные свойства двойного интеграла
- •17) Двойной интеграл в полярных координатах
- •19) Понятие о числовом ряде
- •Свойства сходящихся рядов
- •Доказательство
- •23) Признак Даламбера
- •Обобщенный гармонический ряд
- •Сумма ряда
- •30) Функциональные ряды
- •Степенные ряды
- •32. Интервал и радиус сходимости
- •33. Свойства степенных рядов
- •35. Разложение некоторых элементарных функций в ряд Маклорена
- •36. Приближенные вычисления значений функций с помощью степенных рядов
5) Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
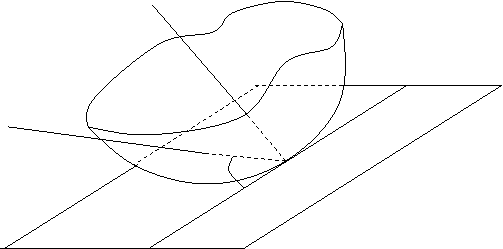
нормаль касательная плоскость
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущейNN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
![]() .
.
Уравнение нормали к поверхности в этой точке:
![]()
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+х, у0+у).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности
![]()
в точке М(1, 1, 1).
![]()
![]()
Уравнение касательной плоскости:
![]()
Уравнение нормали:
![]()
Приближенные вычисления с помощью полного дифференциала.
Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:
![]()
![]()
Если подставить в эту формулу выражение
![]()
то получим приближенную формулу:
![]()
Пример. Вычислить
приближенно значение ![]() ,
исходя из значения функции
,
исходя из значения функции ![]() при x =
1, y =
2, z =
1.
при x =
1, y =
2, z =
1.
Из заданного выражения определим x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01,
z = 1,02 – 1 = 0,02.
Найдем
значение функции u(x, y, z)
= ![]()
Находим частные производные:
![]()
![]()
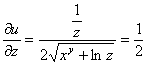
Полный дифференциал функции u равен:
![]()
![]()
Точное значение этого выражения: 1,049275225687319176.
Дискретная математика (конечная математика) - раздел математики, занимающийся изучением свойств объектов конечного характера. К их числу могут быть отнесены, например, конечные группы, конечные графы, некоторые математические модели преобразователей информации.
6) Производная сложной функции
Пусть ![]() --
область в
--
область в ![]() ,
в которой заданы
,
в которой заданы ![]() функций
функций ![]() ,
, ![]() .
Предположим, что все значения вектор-функции
.
Предположим, что все значения вектор-функции
![]()
лежат
в области ![]() ,
в которой задана функция
,
в которой задана функция ![]() .
Тогда можно определить композицию
(или сложную
функцию)
.
Тогда можно определить композицию
(или сложную
функцию) ![]() :
:
![]()
определённую при .
Теорема 7.11 Пусть ![]() --
внутренняя точка области
.
Если в описанной ситуации функции
имеют
в точке
частные
производные
--
внутренняя точка области
.
Если в описанной ситуации функции
имеют
в точке
частные
производные 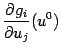 по
переменной
по
переменной ![]() ,
а функция
,
а функция ![]() имеет
в точке
имеет
в точке ![]() частные
производные
частные
производные 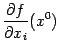 по
всем переменным
по
всем переменным ![]() ,
то сложная функция
имеет
в точке
частную
производную по
,
равную
,
то сложная функция
имеет
в точке
частную
производную по
,
равную
|
(7.7) |
В
частности, если ![]() и
--
интервал вещественной оси
и
--
интервал вещественной оси ![]() и
функции
и
функции ![]() зависят
от единственного переменного
зависят
от единственного переменного ![]() ,
то
,
то
|
(7.8) |
Для
доказательства достаточно выписать
приращения функций и перейти к пределу
при ![]() .
В случае затруднений в таком упражнении
читатель может найти подробное
доказательство (в случае
.
В случае затруднений в таком упражнении
читатель может найти подробное
доказательство (в случае ![]() )
в учебнике
Никольский
С. М. Курс
математического анализа, т. 1. --
М.: Наука, 1991. -- С. 263 - 264.
)
в учебнике
Никольский
С. М. Курс
математического анализа, т. 1. --
М.: Наука, 1991. -- С. 263 - 264.
Производная ![]() от
функции
от
функции ![]() ,
вычисленная по формуле (7.8),
называется полной
производной от
,
вычисленная по формуле (7.8),
называется полной
производной от ![]() по
,
в отличие от частных производных от
по
промежуточным переменным
по
,
в отличие от частных производных от
по
промежуточным переменным ![]() .
.
Пример 7.16
Пусть координаты ![]() зависят
от
зависят
от ![]() следующим
образом:
следующим
образом:
![]()
Рассмотрим функцию
![]()
и
найдём производные величины
по
переменным ![]() и
и ![]() ,
то есть производные композиции
,
то есть производные композиции ![]() .
.
Поскольку
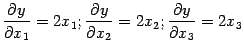
и
|
|
|
|
то по формуле (7.7) получаем:
|
|
|
|
|
|
и
|
|
|
|
|
|
Дифференциалы высших порядков ФНП
Пусть
в области ![]() ,
, ![]() ,
задана произвольная ФНП
,
задана произвольная ФНП ![]() ,
, ![]() ,
имеющая непрерывные частные производные
первого порядка. Полный дифференциал
функции
,
имеющая непрерывные частные производные
первого порядка. Полный дифференциал
функции
![]()
в
общем случае является функцией
переменных ![]() и
приращений
и
приращений ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Если предположить, что 1) функция
.
Если предположить, что 1) функция ![]() имеет
непрерывные частные производные
второго
порядка и 2) для любого
имеет
непрерывные частные производные
второго
порядка и 2) для любого ![]() значения
значения ![]() остаются
произвольными, но постоянными, то можно
рассматривать полный дифференциал
от
остаются
произвольными, но постоянными, то можно
рассматривать полный дифференциал
от ![]() ,
т.е.
,
т.е. ![]() –
дифференциал второго порядка исходной
функции
в
точке
–
дифференциал второго порядка исходной
функции
в
точке ![]() соответственно
соответственно ![]() ,
, ![]() ,
,
,
, ![]() .
.
Пусть ![]() ,
, ![]() .
.
Тогда ![]() .
Поэтому
.
Поэтому
![]()
![]()
![]()
![]() ;
; ![]() –
произвольные.
–
произвольные.
ПРИМЕР
1. Для функции ![]() .
Найти
.
Найти ![]() ,
, ![]() при
произвольных
при
произвольных ![]() и
и ![]() .
.
Решение.
Вычисляем последовательно частные
производные ![]() и
и ![]() ,
а затем
,
а затем ![]() ,
, ![]() ;
; ![]() .
Записываем
.
Записываем
![]() ,
,
здесь
можно также обозначить ![]() ,
, ![]() .
.
Заметим,
что если ![]() записать
в операторной форме
записать
в операторной форме
![]() ,
,
то
для дифференциала второго порядка ![]() можно
использовать запись
можно
использовать запись
![]()
или
![]() ,
,
свернув
оператор формально "в квадрат суммы ![]() ".
".
Можно
убедиться, что при соответствующих
предположениях полный дифференциал
третьего порядка ![]() в
операторной форме запишется
в
операторной форме запишется ![]()
или ![]()
![]()
![]() .
.
Например,
для ![]() (см.
ранее
ПРИМЕР 1) имеем
(см.
ранее
ПРИМЕР 1) имеем ![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
т.е.
,
т.е.
![]() ;
;
здесь , – произвольно заданные постоянные.
По аналогии можно записать
![]() –
–
полный
дифференциал "![]() "-го
порядка для функции
"-го
порядка для функции ![]() .
.
Для
функции ![]() ,
, ![]() имеем
соответственно
имеем
соответственно
![]() ;
;
![]()
![]()
![]() ;
;
аналогично
![]() .
.
Если
х - независимая переменная, то формула
для дифференциала: ![]() .
Если
.
Если ![]() ,
то
,
то ![]() .
Таким образом, независимо от того,
является ли х независимой переменной,
или сама эта переменная х является
функцией другой переменной t, формула
для нахождения дифференциала первого
порядка одна и та же. Это свойство и
называется инвариантностью формы
первого дифференциала, и часто применяется
в теории и решении задач.
.
Таким образом, независимо от того,
является ли х независимой переменной,
или сама эта переменная х является
функцией другой переменной t, формула
для нахождения дифференциала первого
порядка одна и та же. Это свойство и
называется инвариантностью формы
первого дифференциала, и часто применяется
в теории и решении задач.
7) Дифференцирование неявной функции
Функция z = ƒ (х; у) называется неявной, если она задается уравнением
![]()
неразрешенным
относительно z. Найдем частные
производные ![]() неявной
функции z, заданной уравнением (44.11). Для
этого, подставив в уравнение вместо z
функцию ƒ (х; у), получим тождество F(x;у;ƒ
(х; у)) = 0. Частные производные по х и по
у функции, тождественно равной нулю,
также равны нулю:
неявной
функции z, заданной уравнением (44.11). Для
этого, подставив в уравнение вместо z
функцию ƒ (х; у), получим тождество F(x;у;ƒ
(х; у)) = 0. Частные производные по х и по
у функции, тождественно равной нулю,
также равны нулю:
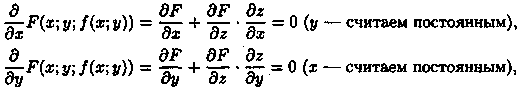
откуда
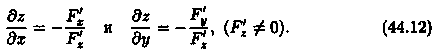
Замечания.
а)
Уравнение вида (44.11) не всегда определяет
одну переменную как неявную функцию
двух других. Так, уравнение х2+у2+z2-4=0
определяет функции![]() определенные
в круге х2+у2≤4,
определенные
в круге х2+у2≤4,![]() определенную
в полукруге х2+у2 ≤ 4 при у≥ 0 и т. д., а
уравнение cos(x + 2у +3z)- 4 = 0 не определяет
никакой функции.
определенную
в полукруге х2+у2 ≤ 4 при у≥ 0 и т. д., а
уравнение cos(x + 2у +3z)- 4 = 0 не определяет
никакой функции.
Имеет место теорема существования неявной функции двух переменных: если функция F(x; у; z) и ее производные F'x(x; у; z), F'y(x; у; z), F'z(x;y;z) определены и непрерывны в некоторой окрестности точки M0(x0;y0;z0), причем F(x0;y0;z0)=0, а F'z(x0;y0;z0)≠0, то существует окрестность точки М0, в которой уравнение (44.11) определяет единственную функцию z=ƒ(х;у), непрерывную и дифференцируемую в окрестности точки (х0;у0) и такую, что ƒ(х0;у0)=z0.
б) Неявная функция у=ƒ(х) одной переменной задается уравнением F(x;у)=0. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
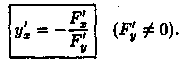
Пример 44.6. Найти частные производные функции z, заданной уравнением ez+z-х2у+1=0.
Решение: Здесь F(x;y;z)=ez+z-х2у+1, F'x=-2ху, F'y = -х2, F'z=ez+1. По формулам (44.12) имеем:
![]()
Пример
44.7. Найти ![]() если
неявная функция у=ƒ(х) задана уравнением
у3+2у=2х.
если
неявная функция у=ƒ(х) задана уравнением
у3+2у=2х.
Решение: Здесь F(x;у) = у3+2у-2х, F'x=-2, F'y = 3у2+2. Следовательно,
![]()
8)
Дифференциалом порядка n,
где n
> 1 от
функции ![]() в некоторой точке называется дифференциал
в этой точке от дифференциала порядка (n —
1),
то есть
в некоторой точке называется дифференциал
в этой точке от дифференциала порядка (n —
1),
то есть
![]() .
.