
- •Частные производные
- •Полное приращение и полный дифференциал
- •Частные производные высших порядков
- •Доказательство
- •5) Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •6) Производная сложной функции
- •Дифференциал высшего порядка функции одной переменной
- •Дифференциал высшего порядка функции нескольких переменных
- •Неинвариантность дифференциалов высшего порядка
- •Дополнения
- •Решение
- •Описание метода
- •Обоснование
- •Двумерный случай
- •Двойной интеграл обозначается
- •4. Некоторые свойства двойного интеграла.
- •5. Вычисление двойного интеграла. Пусть область
- •15) Основные свойства двойного интеграла
- •17) Двойной интеграл в полярных координатах
- •19) Понятие о числовом ряде
- •Свойства сходящихся рядов
- •Доказательство
- •23) Признак Даламбера
- •Обобщенный гармонический ряд
- •Сумма ряда
- •30) Функциональные ряды
- •Степенные ряды
- •32. Интервал и радиус сходимости
- •33. Свойства степенных рядов
- •35. Разложение некоторых элементарных функций в ряд Маклорена
- •36. Приближенные вычисления значений функций с помощью степенных рядов
32. Интервал и радиус сходимости
Рассмотрим
![]() функцию .
Ее областью определения является
множество тех значений x,
при которых ряд сходится. Область
определения такой функции
называется интервалом
сходимости.
Если
интервал сходимости представляется в
виде
функцию .
Ее областью определения является
множество тех значений x,
при которых ряд сходится. Область
определения такой функции
называется интервалом
сходимости.
Если
интервал сходимости представляется в
виде ![]() ,
где R
> 0,
то величина R называется
радиусом
сходимости.
Сходимость ряда в конечных точках
интервала проверяется отдельно.
Радиус
сходимости можно вычислить, воспользовавшись
радикальным признаком Коши, по формуле
,
где R
> 0,
то величина R называется
радиусом
сходимости.
Сходимость ряда в конечных точках
интервала проверяется отдельно.
Радиус
сходимости можно вычислить, воспользовавшись
радикальным признаком Коши, по формуле
![]()
или на основе признака Даламбера:
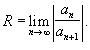
пример:
Найти
радиус и интервал сходимости степенного
ряда 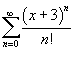 .
.
Решение.
Сделаем
замену: u
= x + 3.
Тогда ряд принимает вид ![]() .
Вычислим радиус сходимости:
.
Вычислим радиус сходимости:
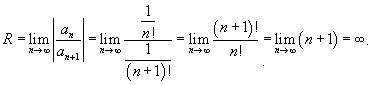
Соответственно, интервал сходимости равен (− ∞; ∞).
33. Свойства степенных рядов
Степенной
ряд (1.2) представляет собой функцию ![]() ,
определенную в интервале сходимости
,
определенную в интервале сходимости ![]() ,
т. е.
,
т. е.
![]() .
Свойство1. Функция
является
непрерывной на любом отрезке
.
Свойство1. Функция
является
непрерывной на любом отрезке ![]() ,
принадлежащем интервалу сходимости Свойство
2. Функция
дифференцируема
на интервале
,
и ее производная
,
принадлежащем интервалу сходимости Свойство
2. Функция
дифференцируема
на интервале
,
и ее производная ![]() может
быть найдена почленным дифференцированием
ряда (1.2), т. е.
может
быть найдена почленным дифференцированием
ряда (1.2), т. е.
![]()
![]() ,для
всех
,для
всех ![]() .
.
Свойство 3. Неопределенный интеграл от функции для всех может быть получен почленным интегрированием ряда (1.2), т. е.
![]()
![]() для
всех
.
для
всех
.
34 Ряды Тейлора и Маклорена.
Теорема
если
в интервале ![]() функция
имеет
производные любого порядка и все они
по абсолютной величине ограничены одним
и тем же числом, т. е.
функция
имеет
производные любого порядка и все они
по абсолютной величине ограничены одним
и тем же числом, т. е. ![]() ,
то ряд Тейлора этой функции сходится
к
для
любого х из этого интервала
,
т. е. имеет место равенство
,
то ряд Тейлора этой функции сходится
к
для
любого х из этого интервала
,
т. е. имеет место равенство
![]() .
.
Для выяснения выполнения этого равенства на концах интервала сходимости требуются отдельные исследования.
Следует отметить, что если функция разлагается в степенной ряд, то этот ряд является рядом Тейлора (Маклорена) этой функции, причем это разложение единственно.
35. Разложение некоторых элементарных функций в ряд Маклорена
1. ![]() .
Для этой функции
.
Для этой функции ![]() ,
, ![]() .
По формуле (3.2) составим ряд Маклорена
данной функции:
.
По формуле (3.2) составим ряд Маклорена
данной функции:
![]() .
(3.3) Найдем радиус сходимости ряда (3.3)
по формуле (1.3):
.
(3.3) Найдем радиус сходимости ряда (3.3)
по формуле (1.3):
![]() .Следовательно,
ряд (3.3) сходится при любом значении
.Следовательно,
ряд (3.3) сходится при любом значении ![]() .Все
производные функции
.Все
производные функции ![]() на
любом отрезке
на
любом отрезке ![]() ограничены,
т. е
ограничены,
т. е
![]() .
Поэтому,
согласно теореме 3.1, имеет место разложение
.
Поэтому,
согласно теореме 3.1, имеет место разложение
![]() .
.
36. Приближенные вычисления значений функций с помощью степенных рядов
Для вычисления приближенного
значения функции f (x)
в ее разложении в степенной ряд сохраняют
первые n членов
(n –
конечная величина), а остальные члены
отбрасывают. Для оценки погрешности
полученного приближенного значения
необходимо оценить сумму отброшенных
членов.
Если данный ряд
знакопостоянный, то ряд, составленный
из отброшенных членов, сравнивают с
бесконечно убывающей геометрической
прогрессией.
Если данный ряд
знакочередующийся и его члены удовлетворяют
признаку Лейбница, то используется
оценка ![]() ,
где un+1
– первый из отброшенных членов
ряда.
Для вычисления
логарифмов эффективна формула
,
где un+1
– первый из отброшенных членов
ряда.
Для вычисления
логарифмов эффективна формула
![]() .
.
Ряд в квадратных скобках сходится тем быстрее, чем больше t.
Пример 1. Оценить погрешность приближенного равенства
![]() ,
, ![]() .
.
37) Этот небольшой урок позволит не только освоить типовую задачу, которая довольно часто встречается на практике, но и закрепить материалы статьи Разложение функций в степенные ряды. Нам потребуется таблица разложений функций в степенные ряды, которую можно раздобыть на странице Математические формулы и таблицы. Кроме того, читатель должен понимать геометрический смысл определенного интеграла и обладать элементарными навыками интегрирования.
На уроке Определенный интеграл. Как вычислить площадь фигуры? речь шла о том, что определенный интеграл – это площадь. Но в некоторых случаях интеграл является очень трудным или неберущимся, поэтому соответствующую площадь в большинстве случаев можно вычислить только приближенно.
Например:
вычислить определенный интеграл 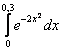 .
Такой интеграл является неберущимся,
но геометрически всё хорошо:
.
Такой интеграл является неберущимся,
но геометрически всё хорошо:
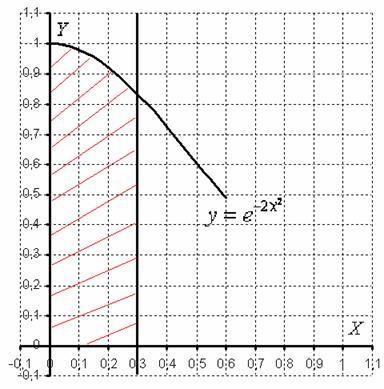
Мы видим, что
подынтегральная функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() ,
а значит, площадь существует, и определенный
интеграл
численно
равен заштрихованной площади. Беда
только в том, что данную площадь
можно вычислить лишь приближенно с
определенной точностью.
На основании вышеизложенных фактов и
появилась типовая задача курса высшей
математики.
,
а значит, площадь существует, и определенный
интеграл
численно
равен заштрихованной площади. Беда
только в том, что данную площадь
можно вычислить лишь приближенно с
определенной точностью.
На основании вышеизложенных фактов и
появилась типовая задача курса высшей
математики.
Пример 1
Вычислить приближенно определенный интеграл, предварительно разложив подынтегральную функцию в ряд Маклорена, с точностью до 0,001
Решение: Идея метода состоит в том, чтобы заменить подынтегральную функцию соответствующим степенным рядом.
Поэтому на первом этапе нужно разложить подынтегральную функцию в ряд Маклорена. Эту распространенную на практике задачу мы очень подробно рассмотрели на урокеРазложение функций в степенные ряды. Кстати, рекомендую всем прочитать, поскольку некоторые вещи, о которых пойдет вещь, могут показаться малопонятными.
Используем
табличное разложение:
![]() В
данном случае
В
данном случае ![]()
![]()
Обратите
внимание, как я записал ряд. Специфика
рассматриваемого задания требуетзаписывать
только несколько первых членов ряда.
Мы не пишем общий член ряда ![]() ,
он здесь ни к чему.
,
он здесь ни к чему.
Чем больше членов ряда мы рассматриваем – тем лучше будет точность. Сколько слагаемых рассматривать? Из практики могу сказать, что в большинстве случаев для достижения точности 0,001 достаточно записать первые 4 члена ряда. Иногда требуется меньше. А иногда больше. Когда больше – это несчастный случай, так как, скорее всего, придется переписывать заново задание.
Следует также отметить, что точность до трёх знаков после запятой самая популярная. Также в ходу и другая точность вычислений, обычно 0,01 или 0,0001.
Теперь второй
этап решения:
Сначала меняем
подынтегральную функцию на полученный
степенной ряд:
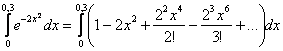
Почему это
вообще можно сделать? Данный факт
пояснялся на уроке Разложение
функций в степенные ряды –
график бесконечного многочлена ![]() в
точности совпадает с графиков функции
!
Причем, в данном случае утверждение
справедливо для любого значения «икс»,
а не только для отрезка интегрования
.
в
точности совпадает с графиков функции
!
Причем, в данном случае утверждение
справедливо для любого значения «икс»,
а не только для отрезка интегрования
.
На следующем
шаге максимально упрощаем каждое
слагаемое:
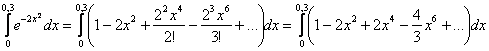
Лучше это сделать сразу, чтобы на следующем шаге не путаться с лишними вычислениями.
После упрощений
почленно интегрируем всю начинку:

Интегралы здесь простейшие, на этом я не останавливаюсь.
На завершающем
этапе вспоминаем школьную формулу
Ньютона-Лейбница 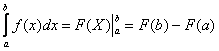 .
Для тех, кто не смог устоять перед
Ньютоном и Лейбницем, есть урок Определенные
интегралы. Примеры решений.
.
Для тех, кто не смог устоять перед
Ньютоном и Лейбницем, есть урок Определенные
интегралы. Примеры решений.
Техника вычислений стандартна: сначала подставляем в каждое слагаемое 0,3, а затем ноль. Для вычислений используем калькулятор:

Заметьте, что
для решения хватило первых трёх членов
ряда, поскольку уже третий
член ![]() меньше
требуемой точности 0,001.
Данный член ряда обычно не приплюсовывают
к результату, именно поэтому для
окончательного расчёта выбраны только
первые два числа:
меньше
требуемой точности 0,001.
Данный член ряда обычно не приплюсовывают
к результату, именно поэтому для
окончательного расчёта выбраны только
первые два числа: ![]() .
.
Ответ: 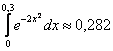 ,
с точностью до 0,001
,
с точностью до 0,001
Что это
получилось за число с геометрической
точки зрения? ![]() –
это приблизительная площадь заштрихованной
фигуры (см. рисунок выше).
–
это приблизительная площадь заштрихованной
фигуры (см. рисунок выше).
Отметим еще
один факт: ![]() –
каждый следующий член ряда по модулю
(без учёта знака) меньше, чем предыдущий.
Почему члены ряда неизбежно убывают по
модулю? Потому-что полученное нами
разложение в ряд сходится к
функции
на
отрезке интегрирования
.
–
каждый следующий член ряда по модулю
(без учёта знака) меньше, чем предыдущий.
Почему члены ряда неизбежно убывают по
модулю? Потому-что полученное нами
разложение в ряд сходится к
функции
на
отрезке интегрирования
.
