9)Метрические пространства и координатный метод представления объектов:

Метри́ческим простра́нством называется множество, в котором определено расстояние между любой парой элементов.

Метрическое пространство есть множество точек с фиксированной функцией расстояния (также называется метрикой) , где обозначает множество вещественных чисел. Для любых точек из эта функция должна удовлетворять следующим условиям:

(аксиома тождества).

(аксиома симметрии).

(аксиома треугольника или неравенство треугольника).

Эти аксиомы отражают интуитивное понятие расстояния. Например, расстояние должно быть неотрицательно, то есть (это вытекает из аксиомы треугольника при ) и расстояние от до такое же, как и от до .

Неравенство треугольника означает, что пройти от до можно короче, или хотя бы не длиннее, чем сначала пройти от до , а потом от до .

10)Двумерные аффинные преобразования координат.

Аффинное преобразование и его матричное представление

Определение. Преобразование плоскости называется аффинным, если

-оно взаимно однозначно;

-образом любой прямой является прямая.

Преобразование называется взаимно однозначным, если

-разные точки переходят в разные;

-в каждую точку переходит какая-то точка.

Однородные координаты

Если рассмотреть параллельный перенос, то оказывается, что для его задания матрицы 2x2 уже недостаточно. Но его можно задать с помощью матрицы размера 3x3. Появляется вопрос, откуда взять третью координату у двумерной точки?

Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.

Однородными координатами вектора (х, у) является тройка чисел (x', y', h), где х = х' / h, у = y'/h, а h — некоторое вещественное число (случай, когда h = 0 является особым).

Прим. Данные координаты не позволяют однозначно задать точку плоскости. Например, (1, 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1). Предлагается взять набор (x, y, 1), который будет описывать все точки плоскости.

Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим некоторые преобразования в однородных координатах.

Сжатие/растяжение

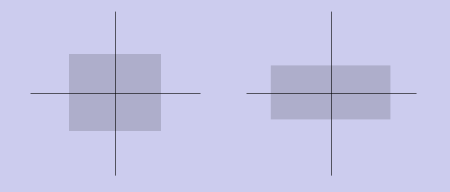
Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (ax * x, ay * y). Матрица преобразования запишется следующим образом:

[ ax 0 0 ]

[ 0 ay 0 ]

[ 0 0 1 ]

Где ax – растяжение по оси x,

ay – растяжение по оси y.

Прим. Можно заметить, что при отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей. Этот случай можно включить в данное преобразование, а можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают только положительные значения.

Поворот

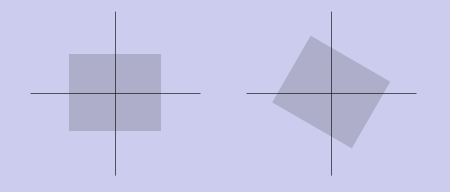
Матрица поворота 2x2 была подробно разобрана ранее. Теперь она дополняется строкой и столбцом:

[ cos(phi) sin(phi) 0 ]

[ -sin(phi) cos(phi) 0 ]

[ 0 0 1 ]

Прим. При угле phi = п эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования).

Параллельный перенос

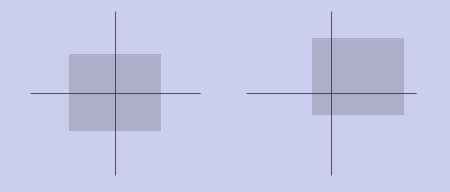
Исходный вектор (x, y) переходит в (x + tx, y + ty). Матрица преобразования запишется следующим образом:

[ 1 0 0 ]

[ 0 1 0 ]

[ tx ty 1 ]

Отражение

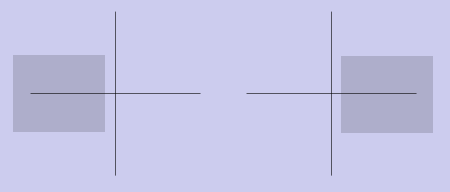
Как говорилось в примечании к преобразованию сжатия/растяжения, отражения получаются следующим образом:

[ -1 0 0 ]

[ 0 1 0 ]

[ 0 0 1 ]

отражение относительно оси x

[ 1 0 0 ]

[ 0 -1 0 ]

[ 0 0 1 ]

отражение относительно оси y

Общий вид аффинного преобразования

Матрица 3x3, последний столбец которой равен ( 0 0 1 )T, задает аффинное преобразование плоскости:

[ * * 0 ]

[ * * 0 ]

[ * * 1 ]

По одному из свойств, аффинное преобразование можно записать в виде:

f(x) = x * R + t,

где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом:

[ R1,1 R1,2 0 ]

[ R2,1 R2,2 0 ]

[ tx ty 1 ]

Если умножить вектор-строку на эту матрицу получаем результат преобразования:

[ x y 1 ] * [ R1,1 R1,2 0 ]

[ R2,1 R2,2 0 ]

[ tx ty 1 ]

=

[ x’ y’ 1 ] + [ tx ty 1 ]

При этом [ x’ y’ ] = R * [ x y ]

Прим. Любопытный читатель уже задал себе вопрос: в чем смысл определителя матрицы R? При аффинном преобразовании площади всех фигур изменяются в |R|.

Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R, и параллельного переноса. Разберем более подробно природу этой матрицы и возможности, которые она нам дает.

Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R1,1, R1,2), вектор (0, 1) переходит в (R2,1, R2,2). Новый базис это строки матрицы R.

Пример.

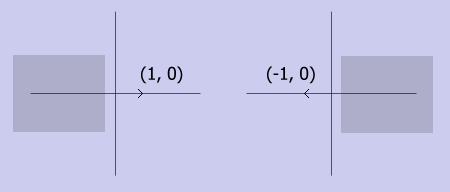
При отражении относительно оси y, базисный вектор по оси ординат сохраняется, а по оси абсцисс переходит в (-1, 0). Т.о. матрица R будет выглядеть следующим образом:

[ -1 0 ]

[ 0 1 ]

Теперь становится ясно, что кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос: