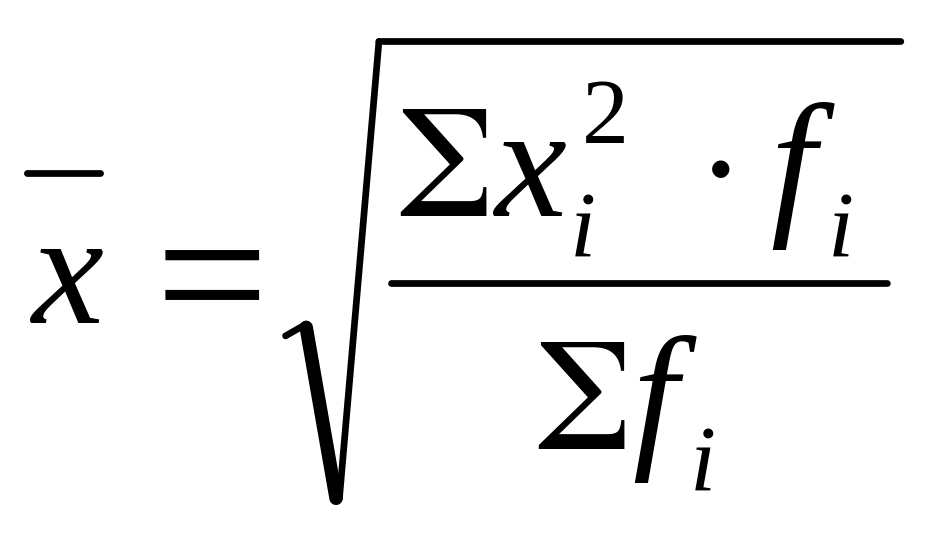- •1. Предмет и метод статистики. Структура статистической науки.
- •2. Закон больших чисел и статистическая закономерность. Статистическая методология.
- •3. Основные категории статистики. Статистические показатели.
- •4. Требования, предъявляемые к сопоставимости статистических данных.
- •5. Основные направления реформирования статистики. Организация статистики в рф.
- •6. Статистическое наблюдение – формы, виды, способы.
- •7. Программно-методологические и организационные вопросы наблюдения.
- •8. Классификация ошибок статистического наблюдения, методы контроля данных.
- •9. Сущность и методология группировки, виды группировок.
- •10. Статистические таблицы, правила построения.
- •11. Ряды распределения, их виды, графическое изображение
- •12. Абсолютные и относительные величины, необходимость комплексного применения
- •13. Средние величины, их сущность. Взаимосвязь метода средних и группировок
- •14. Виды степенных средних, методы их расчета. Свойства средней арифметической.
- •15. Структурные средние. Методы расчета и практика применения
- •16. Графическая форма изображения статистических данных. Виды графиков.
- •17. Вариация, значение ее статистического изучения в условиях рынка.
- •18. Основные показатели вариации, их сравнительный анализ
- •19. Дисперсия альтернативного признака. Свойства дисперсии.
- •20. Ряды динамики, их виды, значение статистического изучения
- •21.Основные показатели динамики. Взаимосвязь цепных и базисных характеристик.
- •22. Средние характр-ки рядов динамики
- •23. Методы определения тренда в рядах динамики, их сравнительная оценка
- •24. Метод аналитического выравнивания (прямая, парабола, гипербола)
- •25. Экстраполяция в рядах динамики. Основные методы
- •26. Оценка сезонности в рядах динамики
- •28. Индексы, их роль в анализе экономических явлений.
- •29. Агрегатная форма – основной вид индекса. Индексы Пааше и Ласпейреса.
- •30. Факторный индексный анализ (2-х и 3-х факторные индексные модели).
- •32. Индексный метод анализа динамики среднего уровня явлений.
- •33. Правило сложения дисперсий. Эмпирическое корреляционное отношение.
- •34. Взаимосвязь экономических явлений. Методы оценки взаимосвязи.
- •35. Корреляционный метод изучения связи.
- •36. Непараметрические методы оценки взимосвязи
- •37. Выборочное наблюдение. Способы отбора единиц из генеральной совокупности.
- •38. Сущность ошибок выборки. Методика расчета при различных методах отбора.
- •39. Предмет, метод и задачи экономической статистики
- •40. Основные категории экономической статистики. Их значение для характеристики экономических процессов
- •Классификация экономических субъектов (по вэд, по секторам экономики), их значение
- •44. Основные показатели снс
- •50. Межотраслевой баланс производства и распределения продукции, задачи построения, схема, основные направления анализа
- •51. Экономическо-математическая модель моб, коэффициенты полных и прямых затрат, значение и направления их использования.
- •52. Статистическая оценка населения
- •53. Статистическая оценка рынка труда
- •57 Статистическая оценка национального богатства
- •59 Статистическая оценка эффективности общественного производства.
- •60. Статистическая оценка уровня жизни населения
14. Виды степенных средних, методы их расчета. Свойства средней арифметической.
Формула средней определяется значением степени применяемой средней. С увеличение показателя степени k возрастает соответственно СВ.
Виды степенных средних:
Виды степенных средних |
простая |
взвешенная |
1) средняя гармоническая (k= -1) |
|
|
2) Средняя геометрическая (k=0) |
|
|
3) Средняя арифметическая (k=+1) |
|
|
4) Средняя квадратическая (k=2) |
|
|
Виды степенных средних |
простая |
взвешенная |
1) средняя гармоническая (k= -1) |
|
|
2) Средняя геометрическая (k=0) |
|
|
3) Средняя арифметическая (k=+1) |
|
|
4) Средняя квадратическая (k=2) |
|
|
![]()
Наиболее известный и распространенный вид средней – арифметическая.
Свойства средней арифметической: 1) сумма отклонений отдельных значений признака от средней арифм =0 Σ(хi-xср)=0.
2)сумма квадратов отклонений значений признака от средней меньше суммы квадратов отклонений от любой произвольной величины Σ(хi-xср)2< Σ(хi-A)2
3) если от каждого значения признака отнять или к каждому его значению прибавить одно какое-л число А, то новая средняя соответственно уменьшится или увеличится на то же самое число
4)произведение средней на сумму частот всегда равно сумме произведений вариантов на частоты: xсрΣf=Σxf
5) если каждое значение признака разделить или умножить на одно и то же число А, то новая средняя соответственно уменьшится или увеличится во столько же раз
6) если значения признака веса разделить или умножить на одно и то же число, то величина средней не изменится

15. Структурные средние. Методы расчета и практика применения
Наиболее часто в экономической практике применяют такие структурные средние, как мода и медиана.
Мода – значение изучаемого признака, повторяющееся с наибольшей частотой. Медиана – значение признака, приходящееся на середину упорядоченной совокупности.
Вычисление моды и медианы зависит от того, какими данными располагают: несгруппированными или сгруппированными.
Для несгруппированных данных: мода отражает наиболее распространенный вариант значений признака. Для определения медианы необходимо построить упорядоченный ряд. При нечетном числе единиц совокупности порядковый номер медианы = (n+1)/2. при четном числе единиц медиана рассчитывается как средняя двух центральных значений.
Для сгруппированных данных и интервальных рр:
![]()
где х0 – начало модального интервала, h – величина модального интервала, f2 – частота модального интервала.
![]()
где х0 – начало медианного интервала, h – величина медианного интервала, fme – частота медианного интервала, Σf/2 – номер медианы (номер нужной единицы сов-ти), Sme-1 – накопленная частота предшествующего интервала.
Ме отражает значение признака, сумма отклонений от которого является наименьшей величиной. Мо – величина, вокруг которой группируется наибольшее количество единиц совокупности.