
- •1. Понятие вектора и лин. Опер. Над вект-ми. Св-ва опер. Слож. Вект-ов и умнож. Вект-а на число (с док-вом)
- •2. Вычитание
- •2. Линейн. Зависимость векторов (опред-е, св-ва с док-вом)
- •3. Th о коллинеарн. Векторах. Th о компланарн. Веторах
- •4. Th о разлож. Вектора по некомпланарн. Векторам. Коорд. Вектора. Ортонормир. Базис.
- •5. Скалярн. Произв-е векторов. Применение скалярн. Произв-я
- •6. Векторное произв-е (опр-е, вычисл-е, св-ва)
- •7. Смешанное произв-е (опр-е, вычисл-е, св-ва)
- •8. Афинная сист. Коорд. На плоск. И в простр. Декарт. Сист. Корд. Деление отрезка в зад. Отношении
- •9. Ориентация плоскости
- •10. Угол м-у векторами на ориентир. Плоск-ти
- •1 Парал. Перенос
- •2 Поворот осей координат
- •3. Изменение нач. Корд. И поворот осей
- •12. Расст. М-у 2-мя т. Деление отрезка в данном отнош-ии. Прямая линия на плоск. Осн. Виды ур-я прямой на плоск.
- •13. Расст. От т. До прямой. Коорд. Т. Пересеч. Двух прямых. Угол м-у двумя прямыми. Услов. Паралл-ти и перп-ти прямых
- •14. Плоск. В пр-ве. Основн. Виды ур-й плоск. В пр-ве. Услов паралл-ти и перп-ти плоск.
- •15. Неполные ур-я плоск. Расст. От т. До плоск.
- •17. Прям. Линия в простр. Основн. Виды ур-я прямой линии в простр. Угол м-у прямыми. Услов. Паралл-ти и перп-ти 2-х прямых.
- •18. Прямая и плоск. Т. Пересеч. Прямой и плоск. Угол м-у прямой и плоск. Услов. Паралл-ти и перп-ти прямой и плоск.
- •19. Эллипс
- •20. Гипербола
- •21. Парабола
- •22. Поверхн. 2-го пор. Поверхн. Вращ-я. Циллиндрич. Поверхн. Конич. Поверхн. 2-го пор.
- •23. Эллипсоид
- •24. Гиперболоид (однополост., двуполост.)
- •25. Параболоиды (эллиптич., гиперболич.)
- •26. Цилиндры (эллиптич., гиперболич., параболич.)
7. Смешанное произв-е (опр-е, вычисл-е, св-ва)
Если
вектор
умнож. векторно на
а результ.
скалярно умнож. на
,
то
получ. число назыв. смеш.
произв-ем
векторов
,
.
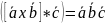
Тh. Смеш. произв-е некомпл. векторов , по абсол. величине равно объёму парал-пипеда, постр. на этих векторах, привед. к одному началу.
Д-во:
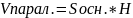 ,
,
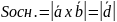
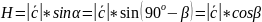
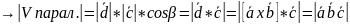
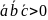 ,
если
,
если
 – прав.
– прав.
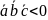 ,
если
- лев.
,
если
- лев.
Следствие 1:
[
]*
=[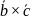 ]*
=
]*
=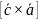 *
,
аоск. тройки векторов
,
*
,
аоск. тройки векторов
,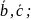 ,
,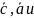 ,
,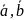 имеют одинак. ориентацию (циклич.
перестан. знака не меняет). Не циклич.
перестан. в смеш. произв. привод.
имеют одинак. ориентацию (циклич.
перестан. знака не меняет). Не циклич.
перестан. в смеш. произв. привод.

Следствие 2 (критерий компланарности 3-х векторов):
Необх. и дост-ным услов. компланарности 3-х векторов явл. рав-во 0 их смеш. произв-я.
,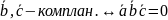
Th.
Если 3 вектора
(x1,y1,z1),
(x2,y2,z2),
(x3,y3,z3)
зад. своими коорд., то смеш. произв.
 =
=

Д-во:
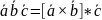
=
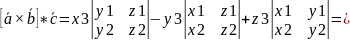
=
Следствие:
,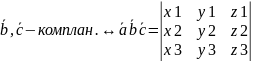
8. Афинная сист. Коорд. На плоск. И в простр. Декарт. Сист. Корд. Деление отрезка в зад. Отношении
В L (мн-во всех векторов, паралл. плоск-ти) сущ. беск. мн-во базисов.
Совокупн.
нек. т. О и базисн. векторов. образ. сист. корд. О
образ. сист. корд. О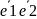 ,
назыв. аффинной
сист. корд.
,
назыв. аффинной
сист. корд.
Коорд-ми
т. М (x,y)
назыв. числа x и y, такие, что
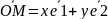 (1), х – абсцисса
т. М, у – ордината т.М
(1), х – абсцисса
т. М, у – ордината т.М
При
выбр. сист. корд. кажд. т. М плоск имеет
корд. x,y,
причем, если т. M1(x1,y1),
M2(x2,y2)
различны, то пары чисел (x1,y1)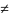 (x2,y2),
т.е. (x1
x2
или y1
y2),
и наоборот, для кажд. упорядоч. пары x,y
можно указ. т., имеющ. данные корд-ты.
(x2,y2),
т.е. (x1
x2
или y1
y2),
и наоборот, для кажд. упорядоч. пары x,y
можно указ. т., имеющ. данные корд-ты.
 ,
,
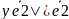 ,
то на осях корд. Ох и Оу сущ. соотв. т.
М1, М2, такие, что
,
то на осях корд. Ох и Оу сущ. соотв. т.
М1, М2, такие, что
 ,
,
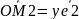 (2)
(2)
Из
(1)
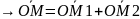 (3)
(3)
Польз. рав-вами (2), строим т. М1, М2.
Проведя ч-з эти т. прямые, парал. корд. осям, находим их т. пересеч., кот согласно ф-ле (3) будет т. М
Пусть в кач-ве базиса выбр. 3 взаимно перп. единичн. вектора
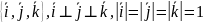 ,
векторы
- базисные орты
,
векторы
- базисные орты
Получ. сист. корд. назыв. прямоуг. декарт. сист. коорд. Коорд. люб. вектора в этом базисе назыв. декарт. коорд. вектора.
Коорд.
т. М в ДСК по осям ОХ,. OY,
OZ
назыв. соотв. абсциссой,
ординатой и аппликатой.

Декартовы прямоуг. корд-ты x,y,z вектора равны проекциям этого вектора на оси OX, OY, OZ:
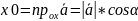 ,
,


где
 - углы, кот. сост. вектор
с корд. осями OX, OY, OZ, при этом
- углы, кот. сост. вектор
с корд. осями OX, OY, OZ, при этом
 назыв. направл. косинусами этого вектора.
назыв. направл. косинусами этого вектора.
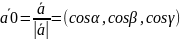 – вектор единичн.
длины и данного направл. вектора
– вектор единичн.
длины и данного направл. вектора
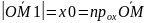 ,
,
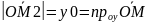

Для
направл. косинусов справ-во соотнош-е
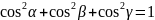
Т.
M(x,y)
делит отрезок M1M2
в отношении λ,
если
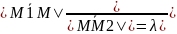
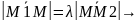

 – коорд. т. М
– коорд. т. М
Если
М – середина М1М2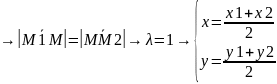
Замечание:
 М1М2
М1М2
9. Ориентация плоскости
10. Угол м-у векторами на ориентир. Плоск-ти
Пусть
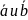 - ненулев. векторы. Отложим от произв.
т. О векторы
- ненулев. векторы. Отложим от произв.
т. О векторы
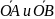 .
Угол м-у лучами ОА и ОВ назыв. углом
м-у векторами
.
.
Угол м-у лучами ОА и ОВ назыв. углом
м-у векторами
.
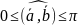
Пусть
заданы в опр. порядке.
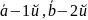
Если
векторы
не коллинеарны, то направл.
(ориентированным) углом м-у векторами
назыв. величина
 ,
если базис
- правый, и
,
если базис
- правый, и
 ,
если левый.
,
если левый.
Если
векторы
одинак. направл., то направл. угол м-у
ними счит. равным 0, а если противоположн.
направл., то

Т.о.
для люб. ненулев. векторов
-
Т.к.
направл. угол
=-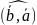 ,
и если векторы
не коллинеарны, то
,
и если векторы
не коллинеарны, то
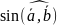 =
-
=
- ,
,
 =cos
,
=cos
,
Если
векторы
 - произв., ненулев., то можно д-ть, что
- произв., ненулев., то можно д-ть, что
= -
=cos
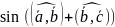 =
=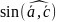
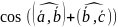 =cos
=cos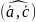
Th.
Коорд-ты (а1,а2) произв. ненулев. вектора
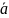 в ортонормир. правом базисе i,j вычисл.
по ф-ле
в ортонормир. правом базисе i,j вычисл.
по ф-ле
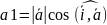
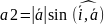
Д-во:
 Обе части скалярно
умнож. на вектор
Обе части скалярно
умнож. на вектор
 .
.
 ,
(
,
(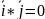 )
)
Следствие:
Единичн.
вектор
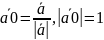 в ортонормир. базисе
в ортонормир. базисе
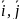 имеет координаты
имеет координаты
 .
.
11. Ф-лы преобраз. корд. на плоск. Преобраз-е прямоуг. сист. корд. Полярные корд.
