1. Понятие вектора и лин. Опер. Над вект-ми. Св-ва опер. Слож. Вект-ов и умнож. Вект-а на число (с док-вом)
Величины, для опр-я кот. дост-но знать одно число, назыв. скаляром.
Геом. вектором назыв. направл. отрезок (характ-ся длиной (модулем) и направл-ем).
Своб. векторы счит. равными, если модули равны и направл. одинак. Вектора не явл. своб., если сущ. т. приложения вектора или линия действия вектора (связанные и скользящие.)
Длиной
вектора назыв. расстояние от нач. к
концу вектора.
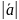
Нулевым
вектором
назыв. вектор, у кот. начало и конец
совпад.
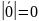
Векторы назыв. коллинеарными, если лежат на одной прямой, либо на парал. прямых. Нулевой вектор коллинеарен люб. вектору.
3 вектора назыв. компланарными, если они лежат в одной плоск., либо в парал. плоск-ях. Если тройка векторов содерж. нулевой вектор или пару коллинеарн. векторов, то эти векторы комплан.
Два
вектора равны,
если они коллинеарны, имеют одинак.
длину и направл-е.
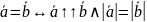
Линейные операции
1.
Суммой векторов
и
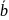назыв. вектор
+
=
,
идущ. из нач. вектора
в конец вектора
,
при услов., что нач.
приложено к концу
(правило треуг.)
Св-ва:
1.
+
=
2.
(
+
)+
=
+(
+
3.
(Ǝ
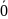)(ᵾ
)(
+
)
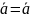4.
Правило парал-ма:
Если и прилож. к общ. началу, то сумма этих векторов предст. собой диагональ парал-ма, идущ. из их общ. начала.
2. Вычитание
1 сп. - = +(- )
2
сп.
-
=
,
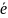3.
Произведение
на действ. число kϵR
есть вектор k*
=
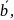коллин. к вектору
,
|
|=|k*
|=|k|*|
|
и направление
сонаправлен. с
,
если k>0;
противоп. направлен. с
,
если k<0
Св-ва:
1.
k*(
+
)=
+
,
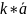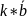kϵR
2. *(λ+β)= *λ + *β, λ,β ϵR
3. λ*(β* )=(λ*β)
4. 1* =
1. Д-ва:
1.
,
,
+
=
+
=
=
,
=
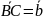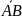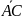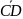ABCD
– парал-м, (
||
и |
|=|
|)
=>
+
=
=
=
2.
,
,
+
=
+
=
,
=
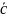
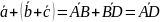
3. Д-во вытек. из опр-й суммы векторов и нулевого вектора.
4.
Дост-но опр.
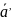как вектор, коллин. вектору
,
имеющий одинак. с ним длину и противоп.
направл. Очевидно, что по правилу треуг.
их сумма дает
.
3. Д-ва:
1. -----
2. -----
3. -----
4.-----
+ док-ва и графики на обратн. сторону
2. Линейн. Зависимость векторов (опред-е, св-ва с док-вом)
Линейной
комбинацией векторов
ϵV
назыв. вектор
вида
=
λ1*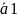
+λ2*
+..+λn*
,
где λ1,λ2,..,λn
ϵ R
Векторы
в. п. V
назыв. ЛЗ
если найд. такие скаляры λ1,λ2,..,λn,
из кот. хотя бы 1 отлично от нуля, что
линейн. комбинация векторов
равна
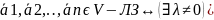λ1*
+λ2*
+..+λn*
=
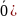
Векторы в. п. V назыв. ЛНЗ если линейн. комбинация этих векторов равна только при услов. что λ1=λ2=…=λn=0
Св-ва:
1. Если сист. векторов содерж. , то она ЛЗ.
2. Если среди n векторов какие-либо (n-1) ЛЗ, то и все n векторов ЛЗ.
3. -----
4. -----
5. -----
6. -----
7. -----
Д-ва:
1. -----
2. -----
3. -----
4. -----
5. -----
6. -----
7. -----