15) Опр. Функция называется непрерывной в точке , если она определена в этой точке и ее значение равно пределу функции в этой точке:

Если обозначить (приращение аргумента),

(приращение функции), то равенство можно записать в виде , т.е. если функция непрерывна в точке , то бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.

Свойства функции непрерывности в точке:

- Если функции и непрерывны в точке , то их алгебраическая сумма, произведение и частное являются функциями непрерывности в точки .

- Если функция непрерывна в точке , а функция непрерывна в точке , то сложная функция непрерывна в точке .

16) Если в точке функция не является непрерывной, то эта точка называется точкой разрыва функции. Опр. Точка называется точкой устранимого разрыва функции если функция имеет конечный предел не равный значению функции:

Опр. Точка называется точкой разрыва первого рода функции , если в этой точке функция имеет конечные, неравные друг другу пределы слева и справа:

Величина, называется скачком функции в точке разрыва первого рода .

Опр. Точка называется точкой разрыва второго рода функции , если в этой точке, хотя бы один из односторонних пределов функции не существует или равен .

17) Если функция непрерывна в каждой точке интервала , то она называется непрерывной в интервале .

Если кроме этого функция непрерывна в точке справа, т.е. 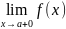, а в точке слева, т.е. 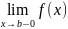, то она называется непрерывной на отрезке .

Теорема Вейерштрасса: если функция непрерывна на отрезке , то она достигает на этом отрезке наименьшего и наибольшего значений. Из теоремы следует, что если функция непрерывна на отрезке , то она ограничена на этом отрезке.

Теорема Больцано-Коши: если функция непрерывна на отрезке и на концах его имеет значения противоположные по знаку, то обращается в по крайней мере, в одной точке интервала .

Геометрический смысл теоремы: график непрерывной функции, соединяющий точки в разных полуплоскостях относительно оси обязательно пересечет ось, по крайней мере, в одной точке.

Функция, имеющая разрыв хотя бы в одной точке, может перейти от отрицательного значения к положительному и, не обращаясь в .