3. Применение нейронных сетей (нс) для управления

Нейронные сети применяются весьма успешно для идентификации (как показано выше) и управления динамическими объектами. Возможность использования многослойных персептронов как универсальных аппроксиматоров делает их популярными для моделирования нелинейных объектов и создания универсальных (общего назначения) нелинейных регуляторов. Рассмотрим некоторые широко используемые методы применения НС-систем в качестве регуляторов.

3.1. Нейросетевые адаптивные системы управления

Важным приложением нейронных сетей является создание системы управления с обратной связью. Структура этой системы усложняется наряду с нелинейностью объекта другими факторами, как, например, наличие неизмеряемых и случайных возмущений, его структурных и параметрических неопределенностей, ненаблюдаемостью состояний. Удобной для применения стратегией управления таким объектом является адаптивное управление на основе эталонной модели (модели желаемой системы).

3.1.1. Нейросетевая технология адаптивной линеаризации обратной связью

Нейросетевая технология адаптивной линеаризации обратной связью основана на стандартном регуляторе с линеаризацией обратной связью. Технология линеаризации обратной связью создает управляющее воздействие с двумя компонетами. Первая компонента компенсирует (сокращает) нелинейности, входящие в модель ОУ, и вторая компонента является линейной обратной связью по состоянию. Класс нелинейных объектов, к которым эта технология применима, описывается уравнением состояния

(1)

где вектор состояния

(2)

содержит как элементы переменные состояния, и u управляющее воздействие. Чтобы преобразовать нелинейный объект управления, описываемый уравнением (1), в линейный объект, можно использовать управляющее

воздействие

(3)

где векторный коэффициент обратной связи по состоянию и v задающее воздействие.

Подставляя (3) в (1) получаем линейный объект, описываемый линейным дифференциальным уравнением

(4)

свойства которого полностью определяются векторным коэффициентом обратной связи по состоянию.

Если функции и не известны, то можно использовать нейронные сети для реализации стратегии линеаризации обратной связью. Аппроксимируя эти функции за счет использования нейронных сетей и , мы можем переписать управляющее воздействие как

(5)

Цель управления состоит в том, чтобы объект управления отслеживал вектор состояния желаемой системы, описываемой моделью

(6)

Путем подстановки (5) в(1) мы получаем

(7)

Векторная ошибка слежения определяется как

(7а)

и дифференциальное уравнение для ошибки имеет вид

(8)

За счет соответствующего обучения нейронных сетей можно обеспечить сходимость решения данного уравнения. При этом ошибка слежения будет стремиться к нулю с течением времени, если будут малы ошибки аппроксимации функций и .

Применение рассмотренной технологии с использованием уравнений (5) и (7а) показано на рис. 11.

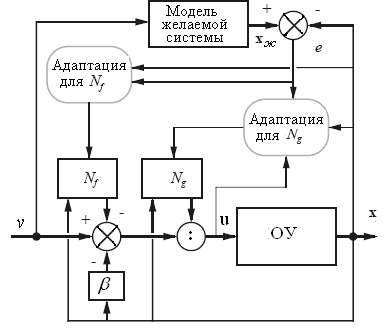
Рис. 11