
- •4. Основные сведения о нейронных сетях
- •4.1. Введение
- •Каждый нейрон, входящий в нейронную сеть и представленный на рис. 1 в виде кружка, участвует в преобразовании входных сигналов, так что выходной сигнал зависит от алгоритма работы всех нейронов.
- •4.2. Модель нервной клетки (нейрона)
- •Лекция 24
- •4.3. Математическая модель нейрона
- •4.4. Многослойная нейронная сеть
- •4.5. Обучение нейронной сети
- •Лекция 25
- •4.6. Обратное распространение ошибки
- •Лекция 26
- •Если q – й нейрон расположен в k–ом скрытом слое (рис. 8), то согласно (17а) при замене r на q , 2 на k, 1 на k-1 и I на r,
- •4.7. Аппроксимация функций (моделирование) с помощью нейронных сетей (персептронов)
- •Нейронная сеть с радиальными базисными функциями
- •Cтруктура нейронной сети с радиально базисными функциями (рбф сети)
- •Методы обучения рбф сети
- •Лекция 27
- •Моделирование (идентификация) нелинейных динамических процессов (объектов)
- •3. Применение нейронных сетей (нс) для управления
- •3.1. Нейросетевые адаптивные системы управления
- •3.1.1. Нейросетевая технология адаптивной линеаризации обратной связью
- •3.1.2. Нейросетевое прямое и косвенное адаптивное управление на основе желаемой (эталонной) модели
- •Лекция 28
- •5. Синтез нейронных нечетких сетей
- •5.1. Введение
- •Адаптивные нейронные нечеткие системы инференции (anfis)
- •Структура anfis
- •Алгоритм обучения anfis
- •Генетические алгоритмы
- •Лекция 29
- •Генетические нечеткие системы (Извлечение нечетких знаний с помощью генетических алгоритмов)
- •Проектирование нечетких систем
- •Классификация генетических нечетких систем
- •4.6. Обратное распространение ошибки
4.6. Обратное распространение ошибки
Метод обратного распространения ошибки представляет собой популярную процедуру обучения многослойного персептрона. Он основан на дельта-правиле и использует критерий качества обучения (сумму квадратов ошибок ej=dj-yj)
(5)
для нейронов выходного слоя. Этот критерий есть сумма квадратов ошибок, получаемых на выходе каждого нейрона выходного слоя.
Весовой коэффициент передачи сигнала от p-го нейрона предыдущего слоя к q-му нейрону последующего слоя обновляется в соответствии с обобщенным дельта-правилом
. (6)
Чтобы обозначения были более понятными, мы опустили индекс обучающего образца k; очевидно, что уравнение (6) является рекуррентным, т.е. в его левой части представляет новое значение весового коэффициента, в то время как в правой части является прежним весом. Здесь - параметр скорости обучения. В обобщенном дельта-правиле корректировка весового коэффициента пропорциональна градиенту ошибки / , другими словами, чувствительности критерия качества к изменению весового коэффициента. Чтобы применить данный алгоритм, необходимы два цикла вычислений, прямое распространение и обратное распространение.
В прямом цикле вычислений веса остаются неизменными. Прямое распространение сигнала начинается в последнем скрытом слое, ведя счет от выходного слоя, путем подачи на его вход образцового входного векторного сигнала и заканчивается в выходном слое после вычисления сигнала ошибки (разности между образцовым выходным сигналом и выходным сигналом нейрона) для каждого нейрона выходного слоя. Обратное распространение сигнала начинается в выходном слое и продолжается путем распространения сигнала ошибки назад справа налево через всю сеть, слой за слоем.
Для описания алгоритма обратного распространения сигнала ошибки предположим, что j – й нейрон является нейроном выходного слоя (рис. 7). На рис. 7 показаны в явном виде связи между нейроном j выходного слоя, нейроном i скрытого слоя 1, нейроном r скрытого слоя 2 и нейроном s скрытого слоя 3.
Рис. 7
Заменяя в (6) q на j и p на i, получаем формулу для настройки весовых коэффициентов выходного слоя
 .
(6а)
.
(6а)
Используя цепное правило дифференцирования, запишем производную, входящую в уравнение (6а), в виде
. (7)
Здесь
с учетом (5)
=
=
-
есть ошибка
j-го
нейрона,
есть выход j-го
нейрона,
![]() (4c)
есть внутренний
вход j-го
нейрона, полученный после суммирования
взвешенных выходов всех нейронов
предшествующего первого скрытого слоя,
в том числе выхода
i-го
нейрона этого слоя,
есть весовой
коэффициент
передачи сигнала от i-го
нейрона первого скрытого слоя к входу
j-го
нейрона выходного слоя. При этом
(4c)
есть внутренний
вход j-го
нейрона, полученный после суммирования
взвешенных выходов всех нейронов
предшествующего первого скрытого слоя,
в том числе выхода
i-го
нейрона этого слоя,
есть весовой
коэффициент
передачи сигнала от i-го
нейрона первого скрытого слоя к входу
j-го
нейрона выходного слоя. При этом
,
где - активационная функция. Как обозначена производная от функции по ее аргументу. С учетом (7) и (4c), находим
, (8)
где
. (8a)
Как видим, для обновления весовых коэффициентов выходного слоя надо найти ошибку , выход i-го первого скрытого слоя и производную .
Найдем формулу для обновления коэффициентов первого скрытого слоя
. (9)
Ошибка j-го нейрона связана с желаемым выходом и очевидно, что = - . Для i-го нейрона первого скрытого слоя в соответствии с методом обратного распространения ошибки мы должны использовать ошибку , т.к. она по аналогии с (7) должна входить в первые две частные производные для . Однако возникает проблема, обусловленная тем обстоятельством, что такая ошибка неизвестна для нейронов скрытого слоя. Чтобы преодолеть эту трудность, определим произведение упомянутых производных непосредственно
. (10)
Частная производная от по выходу i-го нейрона скрытого слоя, прямо связанная с выходом j-го нейрона выходного слоя, определяется как
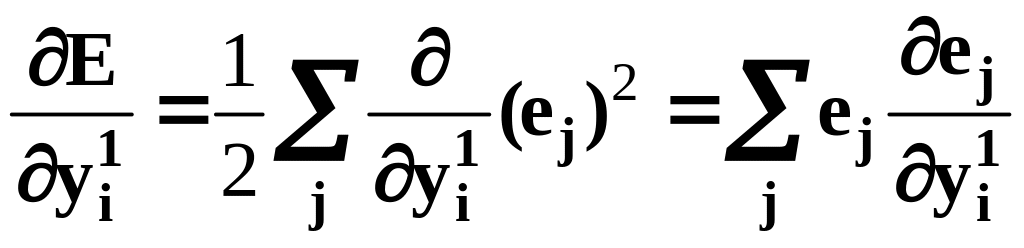 (11)
(11)
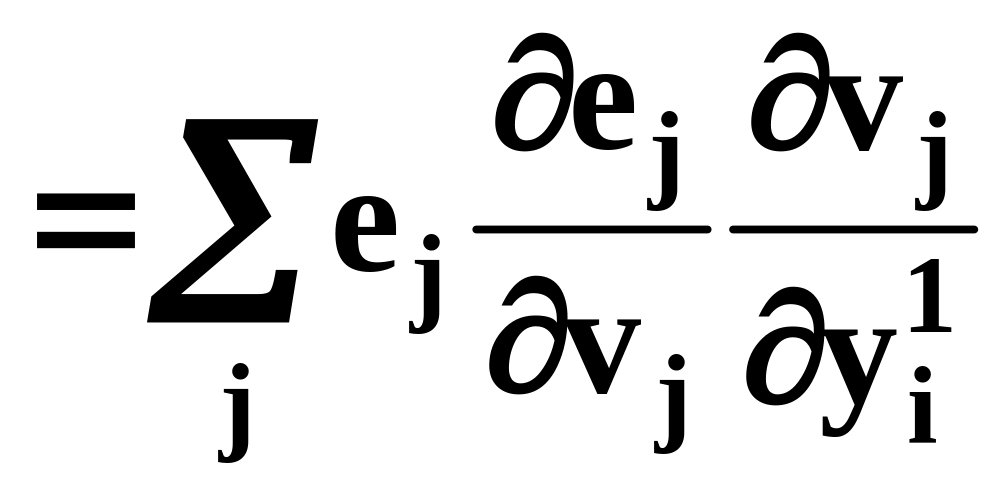 (12)
(12)
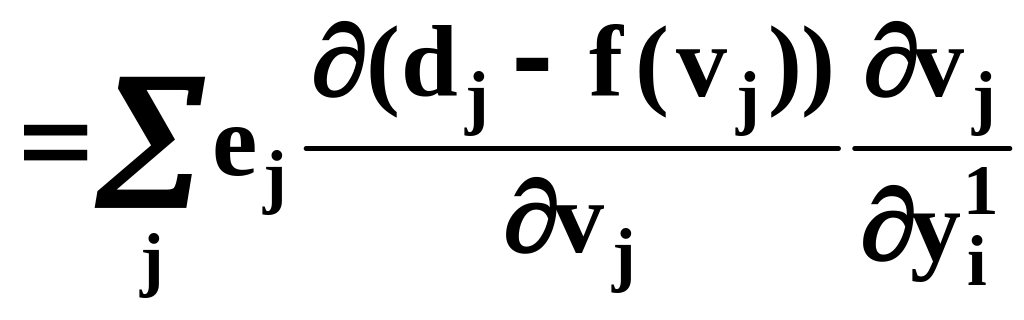 (13)
(13)
![]() .
(14)
.
(14)
Для получения последнего результата принято во внимание (4c).
Используя цепное правило дифференцирования с учетом (14) и
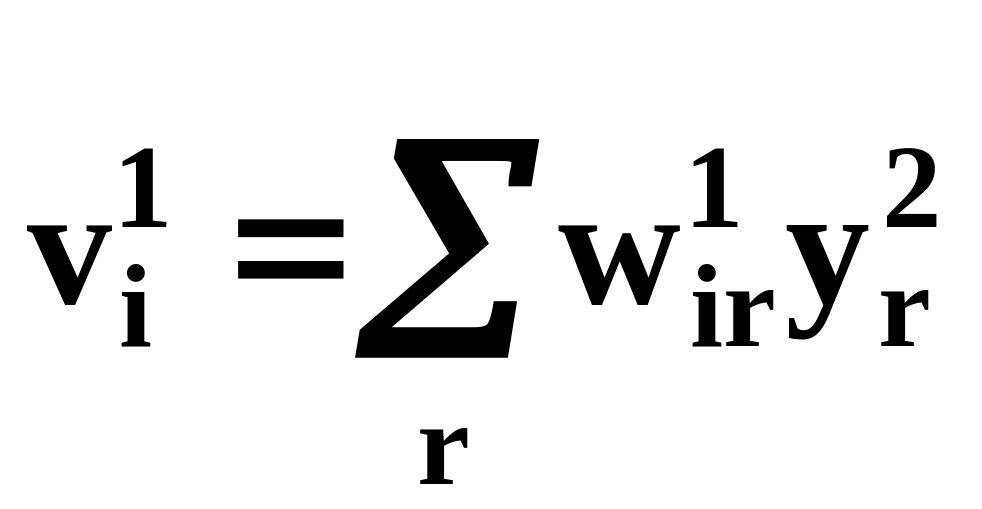 (17),
запишем производную
(17),
запишем производную
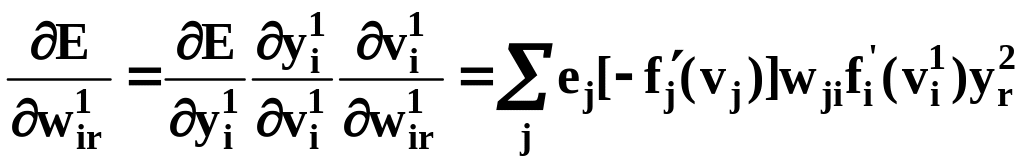 . (15)
. (15)
При этом c помощью дельта-правила (9) получаем формулу для обновление коэффициентов первого скрытого слоя
![]() ,
(16)
,
(16)
где
![]() .
(16а)
.
(16а)
Здесь
i
– номер нейрона первого скрытого слоя,
r
– номер
нейрона второго скрытого слоя,
предшествующего первому скрытому слою,
j
– номер нейрона выходного слоя. Множитель
зависит лишь от
активационной функции
i
–го нейрона скрытого слоя и
.
Значения
содержат весовые
коэффициенты, связанные с нейронами
выходного слоя. Наконец,
есть выход
r
–го нейрона второго скрытого слоя и
этот выход появляется в выражении для
в результате
вычисления производной
![]() /
,
т.к. внутренний
вход i-го
нейрона
равен
/
,
т.к. внутренний
вход i-го
нейрона
равен
. (17)
Как видим, операция суммирования по j требует знания ошибок для всех нейронов выходного слоя. Это говорит о том, что как бы ошибка = - , имеющая место на выходе нейронной сети, «переместилась назад» с выходного слоя на первый скрытый слой.
Для s-го нейрона следующего второго скрытого слоя, предшествующего первому скрытому слою, правило обновления применяется рекуррентно по аналогии с (16) и (16а):
![]() .
(17а)
.
(17а)
Здесь ошибка = - фигурирует в и теперь имеет место перемещение этой ошибки с первого скрытого слоя на второй скрытый слой.
В общем, коррекция (обновление) весового коэффициента , связывающего вход p –го нейрона данного слоя с выходом q – го нейрона предшествующего слоя, определяется как
. (18)
Здесь - параметр скорости обучения, - называется локальным градиентом (сравните с (8), (16) и (17а)) и - входной сигнал q –го нейрона.
Локальный градиент вычисляется рекуррентно для каждого нейрона и его выражение зависит от того, где расположен нейрон в выходном или скрытом слое:
Если q – й нейрон принадлежит выходному слою, то согласно (8а)
. (19)
Оба сомножителя в произведении относятся к q –му нейрону.
Если q – й нейрон расположен в k–ом скрытом слое (рис. 8), то согласно (17а) при замене r на q , 2 на k, 1 на k-1 и i на r
![]() ,h,
(20)
,h,
(20)
где h – число скрытых слоев.
Как
видим,
представляет собой
взвешенную сумму локальных градиентов
нейронов,
расположенных в (k-1)-ом
слое, непосредственно предшествующем
скрытому слою (считая справа налево),
причем
и вычисляется по
формуле (19), а
.
Так при k=1
![]() что
совпадает с (16а) при замене r
на j
и q
на i.
что
совпадает с (16а) при замене r
на j
и q
на i.
Рис. 8
Весовые коэффициенты связей, питающих выходной слой, обновляются за счет использования дельта-правила (18), в котором локальный градиент определяется по выражению (19). Вычислив для всех нейронов выходного слоя, мы затем используем (20), чтобы найти локальные градиенты для всех нейронов следующего слоя и изменить все весовые коэффициенты связей, питающих этот слой. Чтобы можно было вычислить для каждого нейрона, активационная функция всех нейронов должна быть дифференцируемой.
Алгоритм. Алгоритм обратного распространения включает пять шагов.
а) Инициализация весовых коэффициентов. Установите все весовые коэффициенты равными небольшим случайным числам.
б) Предъявление входов и соответствующих им желаемых выходов (обучающие пары). Подаем на нейросеть вектор входа u и соответствующий желаемый вектор выхода d. Вход может быть новым в каждой новой попытке обучения или образцы из обучающего множества могут подаваться на сеть циклически до тех пор, пока весовые коэффициенты не стабилизируются, т.е. перестанут изменяться.
в)
Вычисление
действительных значений выхода.
Вычисляем вектор выхода последовательно
используя выражение
![]() ,
где f
есть вектор активационных функций.
,
где f
есть вектор активационных функций.
г) Настройка весовых коэффициентов. Начинаем настройку с весов выходного слоя и затем идем назад к первому скрытому слою. Весовые коэффициенты настраиваем с помощью
. (21)
В этом уравнении есть весовой коэффициент соединения, связывающего нейрон p скрытого слоя с нейроном q следующего слоя, - выход нейрона p (или внешний вход для нейрона q), есть параметр скорости обучения и - градиент. Если нейрон q является нейроном выходного слоя, то вычисляется с помощью (19) и если нейрон q является нейроном скрытого слоя, то определяется с помощью (20). Ускорение сходимости можно иногда обеспечить, если добавить значение момента.
Пример (локальный градиент). Логистическая (сигмоидная) функция дифференцируема, и ее производная имеет вид . Мы можем исключить экспоненту и записать производную как
. (22)
Для нейрона j в выходном слое мы можем выразить локальный градиент как
. (23)
Для нейрона i скрытого слоя локальный градиент равен
. (24)
Пример (обратное распространение). Чтобы ближе познакомиться с методом обратного распространения ошибки, рассмотрим простой пример с обучающим комплектом данных
u y
-3 0,4 (25)
2 0,8
Пусть нейронная сеть должна иметь один вход, выходной слой, состоящий из одного нейрона и не должна включать скрытых нейронов (рис. 9).
Рис. 9
Чтобы пример был более интересным, выберем для этого нейрона нелинейную активационную функцию, а именно сигмоидную (логистическую) функцию. Выход сети тогда будет иметь вид
![]() . (26)
. (26)
Критерий качества равен
. (27)
С помощью MATLAB/NNET мы можем построить поверхность критерия качества (рис. 10). Инструмент NNET не принимает во внимание коэффициент 1/2 в (27). В процессе обучения веса настраиваются так, чтобы значение критерия качества убывало в соответствии с градиентом. Графическое изображение линий равных значений качества (контур качества) показывает, как перемещается сеть из начальной точки в точку, соответствующую конечному решению. Заметим, что сеть выбирает более или менее крутой спуск.
Значение критерия качества, полученное за каждую эпоху, сохраняется в памяти компьютера и как оно изменяется в зависимости от номера эпохи показано на рис. 11. Значение критерия качества уменьшается в процессе обучения и обучение прерывается после 70 эпох, когда значение критерия становится меньше предварительно установленного уровня. В этой точке
Рис. 10
значения весов равны .
