14. Вычислите стандартизованные коэффициенты регрессии и частные коэффициенты эластичности.
Для
того чтобы сравнить влияние на зависимую
переменную различных объясняющих
переменных, особенно когда эти переменные
имеют различные единицы измерения,
используют также стандартизованные
коэффициенты регрессии
и
коэффициенты
эластичности
(частные
коэффициенты эластичности)
Стандартизованный
коэффициент регрессии
показывает, на сколько величин
изменится в
среднем зависимая переменная y
при увеличении
только i-ой
переменной на
.
а частный коэффициент эластичности
— на сколько
процентов (от средней)
изменится
в среднем y
при увеличении
только переменной
на 1% и
неизменных значениях остальных переменных.
,
,
,
Рис. 17. Стандартизованный коэффициент регрессии и частные коэффициенты эластичности .
15.
Постройте точечный прогноз
для значений переменных на 30%
превышающих их средние значения.
Точечный прогноз вычисляется по формуле
Рис.
18. Точечный прогноз
для значений переменных на 30% превышающих
их средние значения.
16. Вычислите стандартные ошибки прогноза функции регрессии (среднего значения) и индивидуального значения, постройте доверительные интервалы полученных прогнозов. Дайте интерпретацию.
Доверительный интервал прогноза индивидуального значения строится по формуле:
Стандартная
ошибка прогноза индивидуального значения
зависимой переменной вычисляется по
формуле
Матрица
- это матрица – строка, состоящая из 1,
стоящей на первом месте, и прогнозных
значений независимых переменных
,
,
(п. 15, рис. 18).
Рис.
19. Матрица
составлена из 1 и значений
,
,
.
Матрица
это транспонированная матрица
.
Матрица
была получена ранее п. 4.
17. Получите результаты множественного регрессионного анализа с помощью
Пакета Анализа (Tools / Data Analysis …Regression | Сервис/Анализ данных … Регрессия). Использование этой процедуры аналогично расчету параметров парной линейной регрессии, только при указании параметра Входной интервал X следует указать все столбцы, содержащие значения факторов.
В результате выполнения процедуры Регрессия появляются три таблицы
- регрессионная статистика;
- дисперсионный анализ;
- таблица, содержащая коэффициенты регрессии, стандартные шибки, t - статистики и границы доверительных интервалов.
Множественный R – множественный коэффициент корреляции
– выборочный
коэффициент корреляции между фактическими
и расчетными
значениями зависимой переменной. В
случае парной линейной регрессии этот
коэффициент совпадает с выборочным
коэффициентом корреляции
(
)
R-квадрат
– коэффициент детерминации
Нормированный R-квадрат – (скорректированный коэффициент детерминации)
Стандартная ошибка – (выборочное стандартное отклонение остатков)
Наблюдения – n объем выборки.
SSобщ
– общая
сумма квадратов отклонений
фактических значений
от выборочного среднего
, SSобщ=103955.
SSрег
– сумма
квадратов отклонений расчетных значений
от выборочного среднего
,
обусловленная регрессией
,
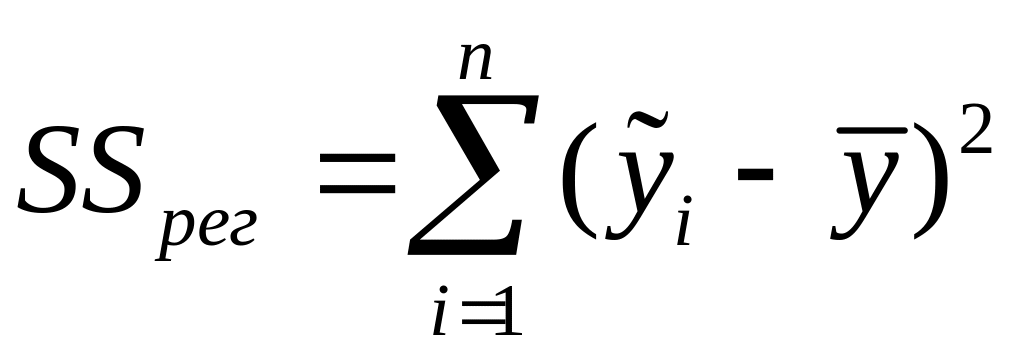SSрег = 93584,5.
SSост
– сумма
квадратов остатков
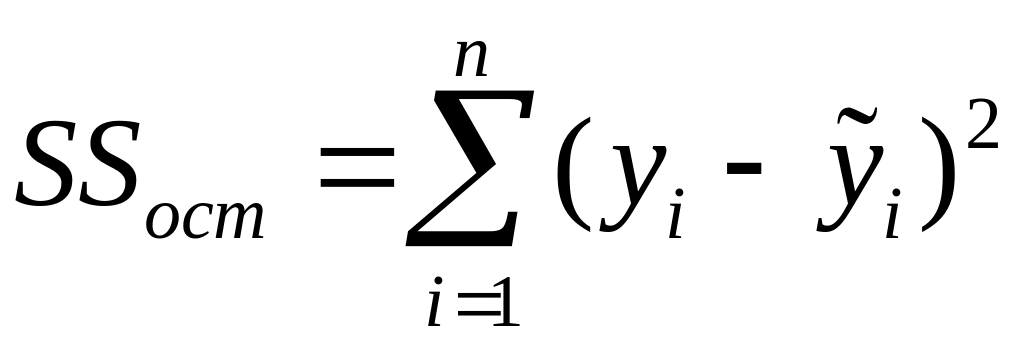
SSост = 10370,1
Эти
суммы связаны равенством
, действительно 93584,5 + 10370,1 = 103955
MSрег
– средний
квадрат регрессии
MSрег = 93584,5
MSост
– средний
квадрат остатков
MSост =370,36
F - статистика, служит для проверки значимость полученного уравнения регрессии в целом по критерию Фишера.
,
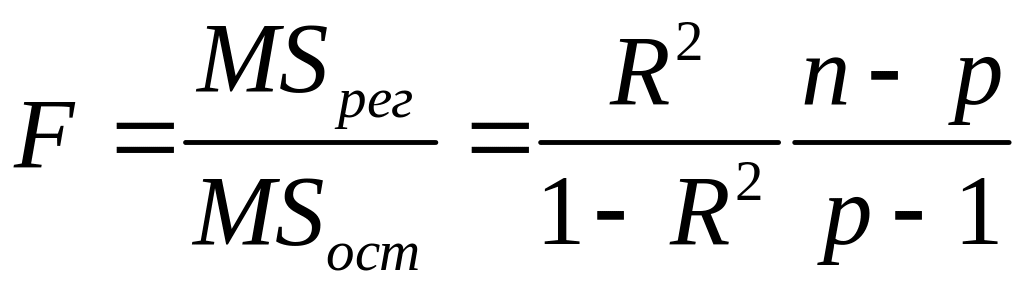F
= 252,685
df – число степеней свободы,
– dfобщ = n – 1 – число степеней свободы суммы
– dfрег = k – 1 – число степеней свободы суммы
– dfост = n – p – число степеней свободы суммы ,
dfобщ = dfрег + dfост
Коэффициенты уравнения регрессии a = 11,23619683 b1 = 3,451143815 b2 =-0,465854629 b3 =2,773033928 |
Стандартная ошибка определения коэффициентов =2,32490564 = 0,295380282 = 0,307132258 =0,465887781 |
t - статистика ta = 10,8372 tb = 15,8961 |
Вероятность ошибки |
Нижние 95% – нижняя
граница доверительного интервала с
доверительной вероятностью 0,95,
Верхние 95% –
верхняя граница доверительного интервала
с доверительной вероятностью 0,95,
