Практическая работа №2

Тема: Множественная линейная регрессия

Цель работы

Построение парной линейной регрессии для каждой переменной и проверка значимости.

Построение множественной линейной регрессии и проверка значимости модели в целом.

Проверка статистической значимость значений коэффициентов регрессии и коэффициента корреляции.

Вычисление доверительных интервалов параметров линейной регрессии.

Построение прогноза и вычисление стандартных ошибок прогноза

Содержание отчета и представление работы

Отчет по работе оформляется в виде файла Excel и должен содержать полученные результаты с необходимыми пояснениями

Задание к работе

Исследуется зависимость курсовой стоимости акций компаний от оборота , прибыли и затрат на новые технологии .

Исходные данные представлены выборкой объема , в папке FREE_ACCESS на pc1 / Эконометрика / Дополнительные материалы / ЗФ / Лабораторная работа_2 / Варианты.

1. Постройте выборочные парные линейные регрессии — оценки зависимости результативного признака от каждого из факторов, рассматриваемого по отдельности.

В каждом случае

— постройте поле корреляции,

— определите коэффициенты уравнения выборочной парной линейной регрессии,

— коэффициент детерминации,

— коэффициент корреляции,

— значение статистики.

Для вычислений воспользуйтесь встроенной функцией LINEST/ЛИНЕЙН.

Напоминание. После того, как будут заполнены все аргументы функции в диалоговом окне ЛИНЕЙН, нажмите комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.

Проверьте статистическую значимость полученных эмпирических парных регрессий. Постройте прямые выборочных регрессий на поле корреляции.

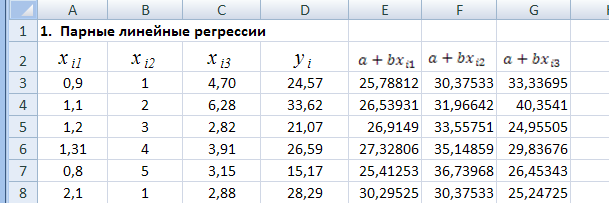
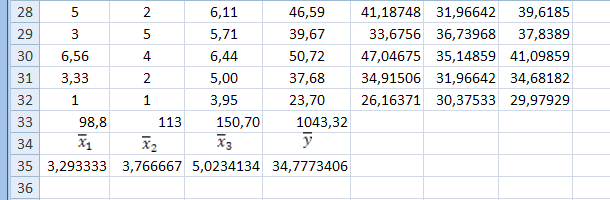
Рис. 1. Исходные данные и значения выборочной парной линейной регрессии , , зависимости результативного признака от каждого из факторов

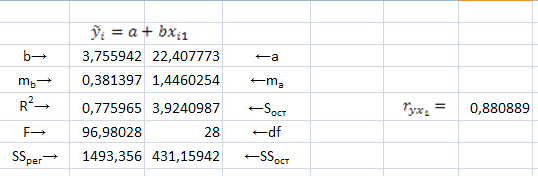
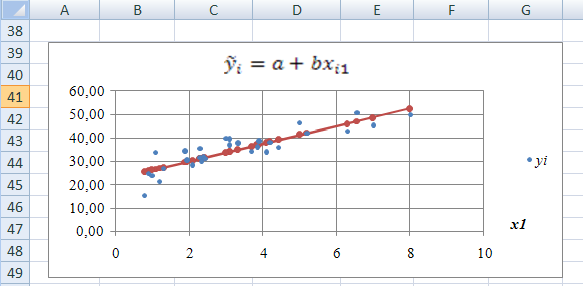
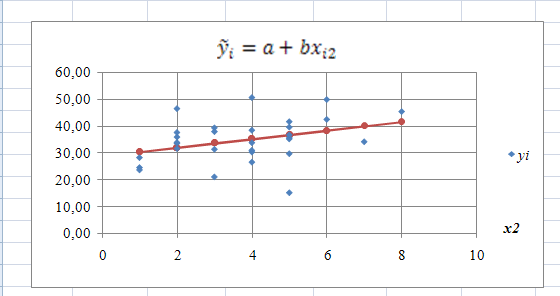
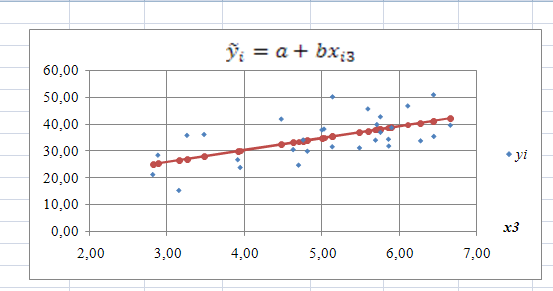
Результаты построения корреляционного поля, линий регрессии и использования встроенной функцией LINEST/ЛИНЕЙН показаны на рис. 2, a), b),c)

a)

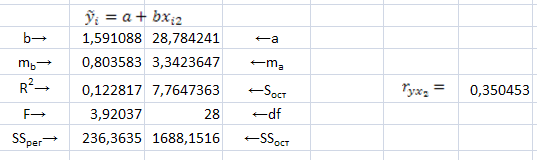
b)

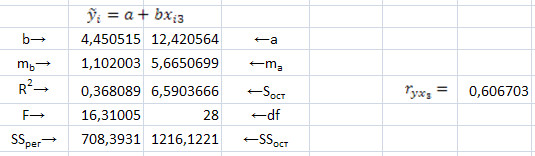
c)

Рис. 2. Результат использования функции LINEST/ЛИНЕЙН и графики выборочных парных линейных регрессий — зависимостей результативного признака от каждого из факторов , и , рассматриваемых по отдельности.

2 . Проверьте мультиколлинеарность факторов.

Построите матрицу вида 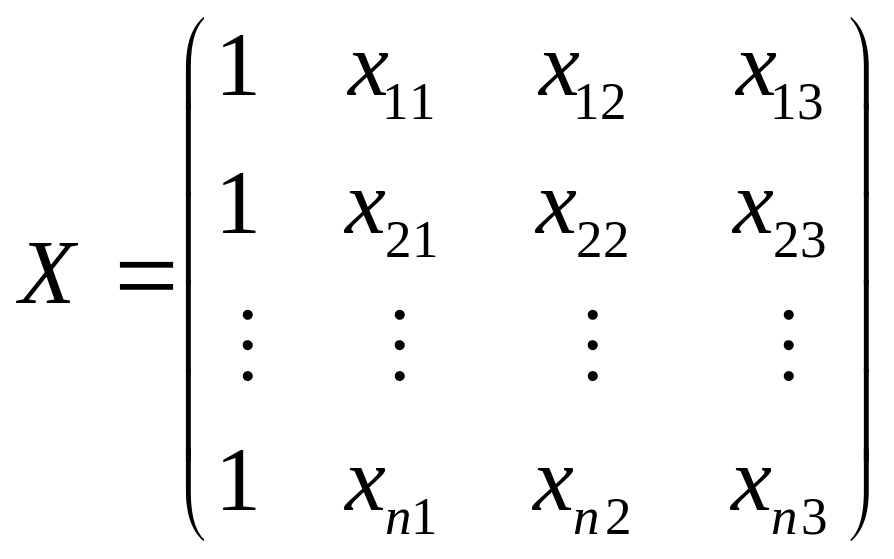, см. рис. 3.

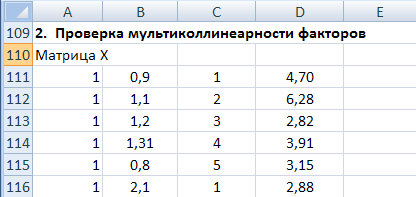
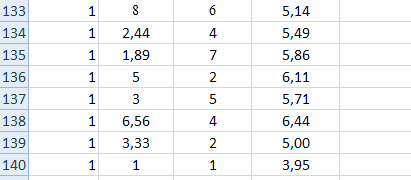
Рис. 3. Матрица X.

Постройте транспонированную к ней матрицу (рис. 4).

Для построения матрицы необходимо предварительно выделить 4 строки и n столбцов и воспользоваться функцией ТРАНСП (категория Ссылки и массивы).

Для активизации функции ТРАНСП используется комбинация клавиш <CTRL> + <SHIFT> + <ENTER>.

n столбцов

Рис. 4. Транспонированная матрица X.

Матрицу умножьте на матрицу .

Произведение матриц вычисляется с помощью функции МУМНОЖ (MMULT), аргументами которой являются перемножаемые матрицы. Перемножаемые матрицы должны удовлетворять условию соответствия размеров: матрица размера может быть умножена справа на матрицу размера , в результате получится матрица размера .

Любые операции с матрицами требуют предварительного выделения области m строк и k столбцов для результата матричной операции.

Активизация матричных операций выполняется использованием комбинация клавиш <CTRL> + <SHIFT> + <ENTER>.

В случае множественной регрессии с тремя факторами матрица X будет иметь размер , матрица — размер , а их произведение — , в нашем случае при .

Вычислите определитель с помощью функции МОПРЕД:

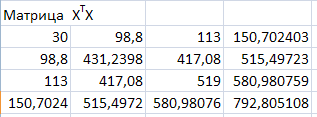
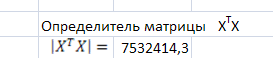
Рис. 5. Матрица и ее определитель = 7532414,3 . Определитель матрицы = 7532414,3 существенно отличается от нуля, следовательно, мультиколлинеарности нет.

3 . Постройте матрицу Q выборочных коэффициентов корреляции (с помощью функции КОРРЕЛ, категория Статистика, или процедуры КОРРЕЛЯЦИЯ пакета Анализ данных).

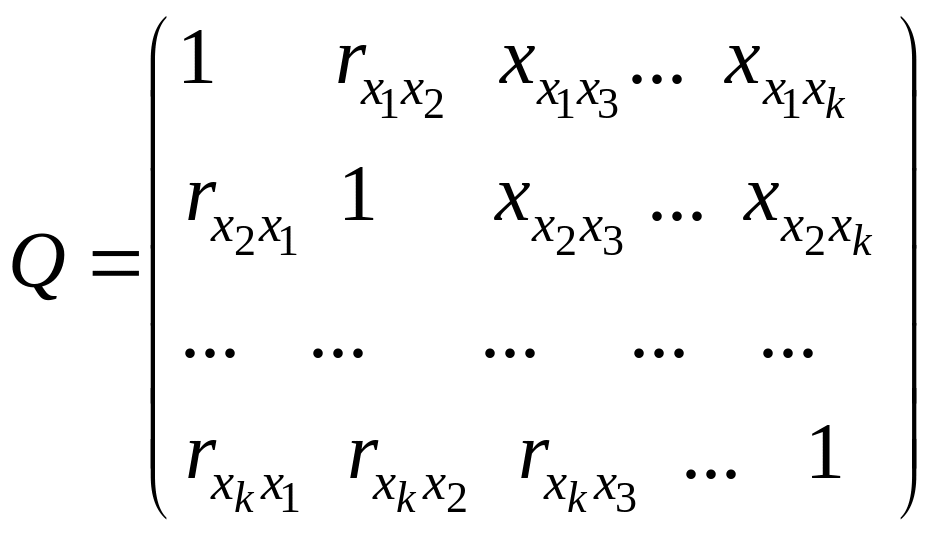
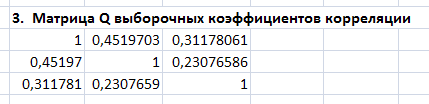
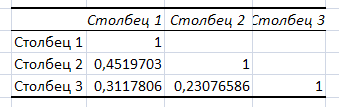
Рис. 6. Матрица выборочных коэффициентов корреляции, построенная с помощью функции КОРРЕЛ (верхняя) и процедуры КОРРЕЛЯЦИЯ пакета Анализ данных (нижняя).

Нет значений больше 0,8, следовательно, нет проблем мультиколлинеарности.

4 . Вычислите коэффициенты выборочной регрессии непосредственно по формуле:

.

Для этого сначала вычислите произведение двух матриц , найдите обратную матрицу , умножьте матрицу на матрицу и, наконец, получить матрицу ;

1 . Матрица уже получена, пункт 2, рис. 5.

2 . Найдите обратную матрицу , функция МОБР, категория Математика;

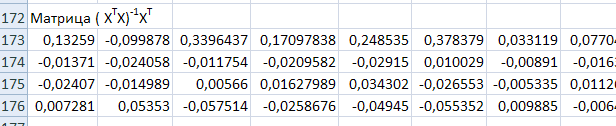
Рис. 7. Матрица .

3 . Умножьте матрицу на матрицу ;

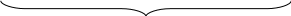
n столбцов

Рис. 8. Матрица .

4 Полученную матрицу умножьте на матрицу-столбец .

Рис. 9. Матрица .

Теперь можно построить выборочное уравнение регрессии .

Напоминание для невнимательных. Функция МУМНОЖ (MMULT) является функцией массива! Поэтому перед использованием функции МУМНОЖ (MMULT) необходимо выделить область размером , в которой будет выведен результат, затем вставить функцию МУМНОЖ, указав ее аргументы. После этого в левой верхней ячейке выделенной области появится первый элемент результирующей матрицы. Для вывода всей матрицы нажмите комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Обратную матрицу вычислите с помощью функции МОБР (MINVERS). Функция МОБР также является функцией массива и ее использование аналогично функции МУМНОЖ: сначала необходимо выделить область ячеек, в которой будет получена обратная матрица, вставить функцию МОБР (MINVERS), затем <CTRL>+<SHIFT>+<ENTER>.

Запишите уравнение регрессии в развернутой форме — дайте интерпретацию коэффициентам выборочной регрессии.

5 . Вычислите коэффициенты регрессии с помощью функции ЛИНЕЙН (LINEST). Для того чтобы использовать эту функцию для вычисления параметров множественной регрессии необходимо:

1) Сначала выделить на рабочем листе область размером , где — число объясняющих переменных – у нас k = 3 (область 54).

2) Затем заполнить поля аргументов этой функции, которые имеют тот же смысл, что и в случае парной регрессии:

Известные_значения_y — адреса ячеек, содержащих значения признака ;

Известные_значения_x — адреса ячеек, содержащих значения всех объясняющих перменых.

Обратите внимание: выборочные значения факторов должны располагаться рядом друг с другом (в смежной области), причем предполагается, что в первом столбце (строке) содержатся значения первой объясняющей переменной, во втором столбце — второй и т.д.

Константа — значение (логическое), указывающее на наличие свободного члена в уравнении регрессии: укажите в поле Константа значение 1, тогда свободный член рассчитывается обычным образом (если значение поля Константа равно 0, то свободный член полагается равным 0);

Статистика — значение (логическое), которое указывает на то, следует ли выводить дополнительную информацию по регрессионному анализу или нет: укажите в поле Статистика значение равное 1, тогда будет выводиться дополнительная регрессионная информация (если Статистика=0, то выводятся только оценки коэффициентов уравнения регрессии);

В случае трех объясняющих переменных результаты расчета параметров регрессии будут выведены в следующем виде:

Таблица 1

Знач. коэфф.	Знач. коэфф.	Знач. коэфф.	Знач. коэфф.
Станд. ошибка коэфф.	Станд. ошибка коэфф.	Станд. ошибка коэфф.	Станд. ошибка коэфф.
Коэффициент детерминации	Оценка – стандартного отклонения остатков
Значение – статистики	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

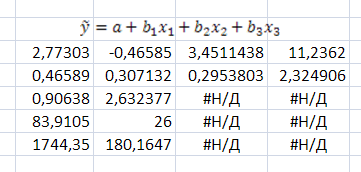
Рис. 10. Коэффициенты регрессии, вычисленные с помощью функции ЛИНЕЙН.

6 . Вычислите множественный коэффициент детерминации и скорректированный (исправленный) коэффициент детерминации непосредственно по формуле

,

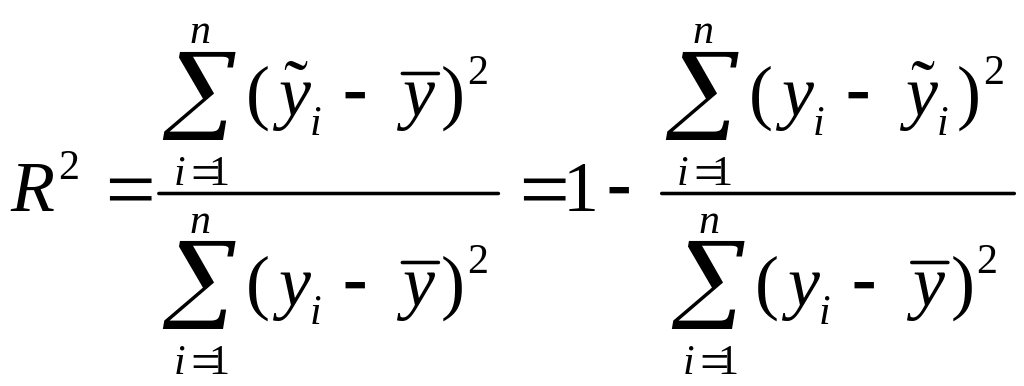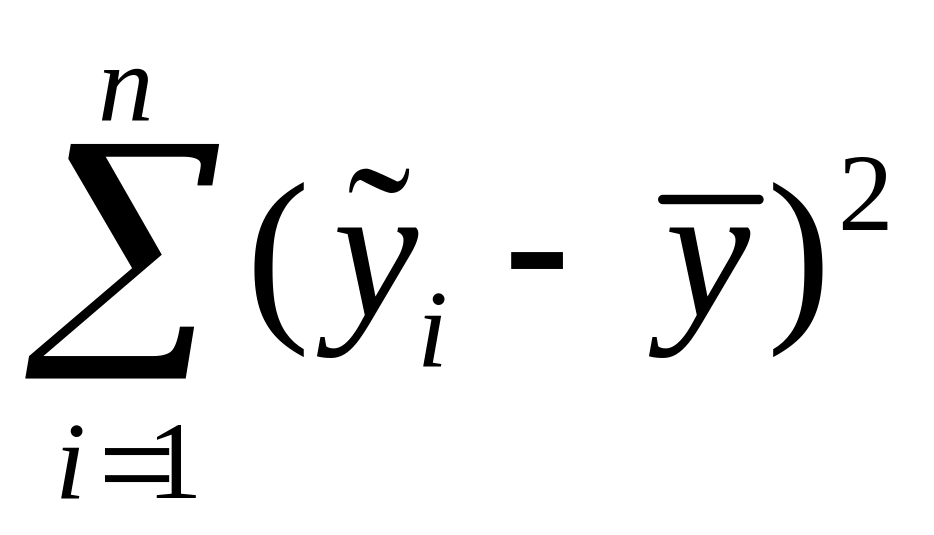– регрессионная сумма квадратов = 1744,351

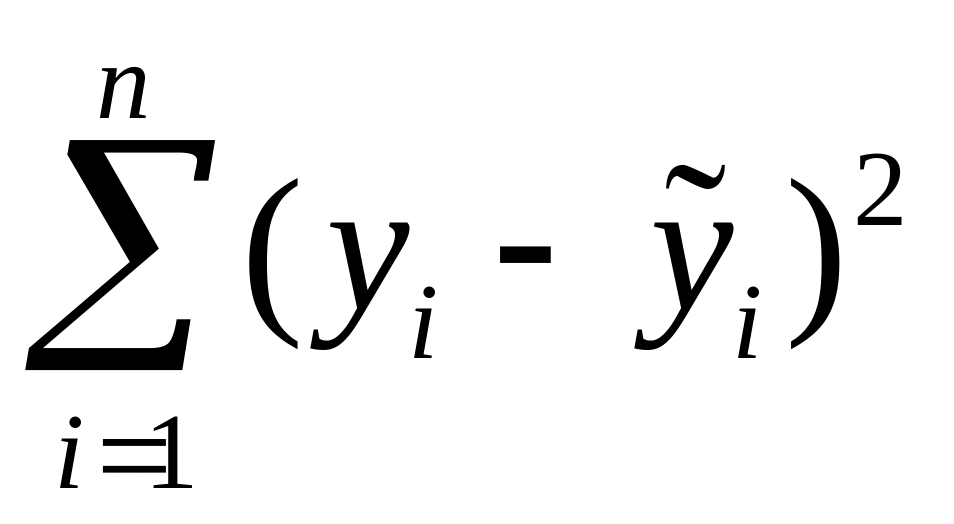– сумма квадратов остатков = 180,1647

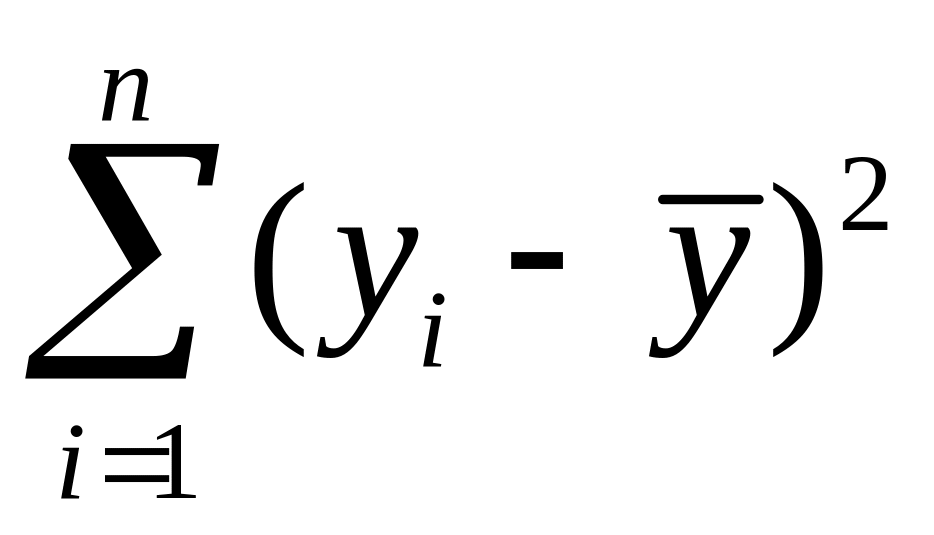– общая (полная) сумма квадратов остатков = 1924,52

Подготовьте вспомогательную таблицу как показано на рис. 11.

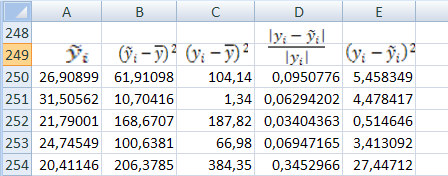
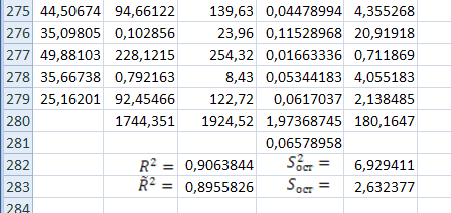
Рис. 11. В ячейке С282 результат вычисления 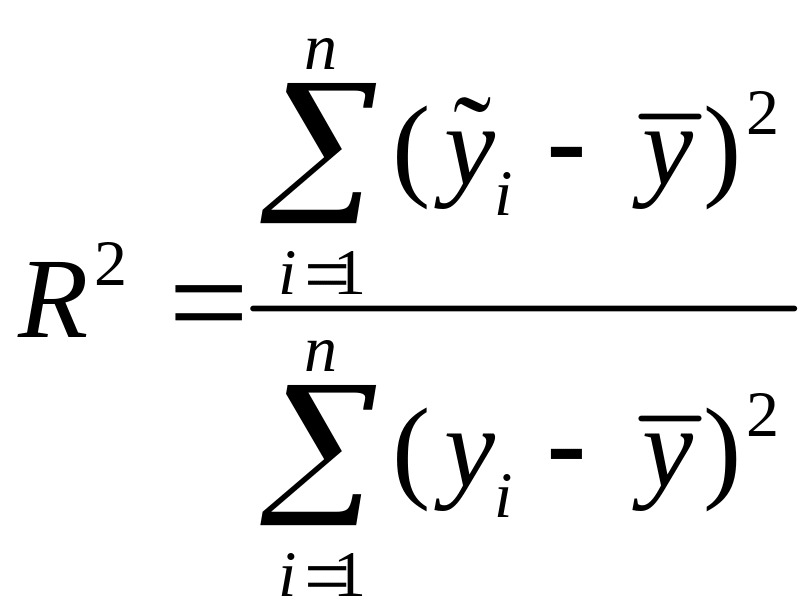= 0,9063844, в ячейке С283 результат вычисления = 0,8955826.

7 . Вычислите расчетные значения согласно найденному уравнению выборочной множественной регрессии (рис. 11, столбец A250:A279).

a = 11,2362, b₁ = 3,451144, b₂ = – 0,465855 b₃ = 2,77034.

8. Вычислите остатки, т.е. отклонения истинных значений признака от расчетных.

9 . Найдите величину средней ошибки аппроксимации и оценку дисперсии остатков .

,

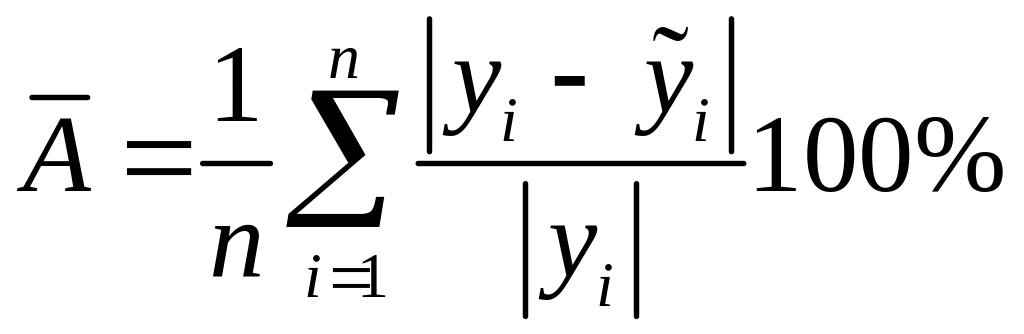Модуль разности вычисляется с помощью функции ABS категории Математика.

Рис. 12. Средняя ошибка аппроксимации .

Результат вычисления остатков = 6,929411, = 2,632377 показан во вспомогательной таблице на рис. 11.

10. Вычислите значение статистики непосредственно по формуле. Проверьте значимость уравнения регрессии в целом используя – тест.

Рис. 13. Статистика F вычислена по формуле .

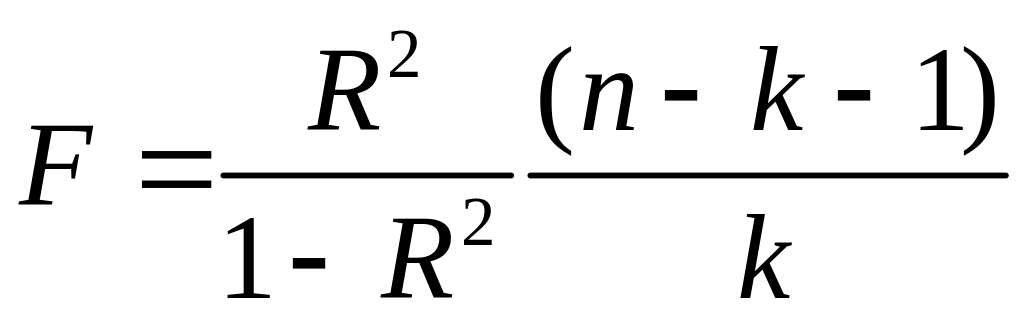определяется по таблице распределения Стьюдента – Снедекора.

Входными величинами в таблицу являются:

– = 0,05 – уровень значимости

– число степеней свободы числителя k – число факторов;

– число степеней свободы знаменателя n – объем выборки;

можно определить с помощью функции .

Проверьте значимость полученного уравнения регрессии в целом по критерию Фишера.

Если выполнены предположения регрессионного анализа, то при выполнении гипотезы (что означает отсутствие взаимосвязи между факторами и y , а так же статистическую незначимость построенной множественной регрессии), то статистика распределена по закону Фишера с числом степеней свободы числителя равном и числом степеней свободы знаменателя равном .

По таблице распределения Фишера - Снедекора при заданном уровне значимости определяется значение как критическая точка при числе степеней свободы числителя равном и числе степеней свободы знаменателя равном .

Тогда:

1) Если , то гипотезу следует отклонить и, следовательно, признать построенное уравнение линейной регрессии статистически значимым,

2) Если , то гипотезу следует принять и, следовательно, признать построенное уравнение статистически незначимым.

Значение можно определить с помощью функции FINV/FРАСПОБР. Аргументы этой функции:

Вероятность — уровень значимости , можно принять равным 0,05 (т.е. 5%);

Степени_свободы1 — число степеней свободы числителя, равно 1 (т.к. один фактор);

Степени_свободы2 — число степеней свободы знаменателя, для парной регрессии равно , где — число наблюдений.

11. Вычислите стандартные ошибки коэффициентов регрессии: , , , непосредственно по формулам. Результаты вычислений показаны на рис. 14.

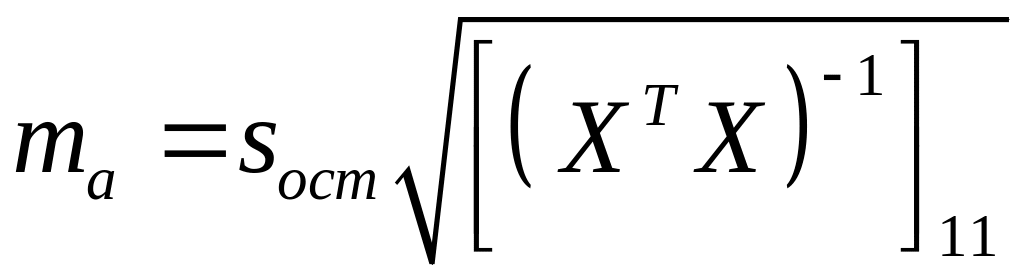– стандартная ошибка коэффициента регрессии ; – первый элемент, стоящий на главной диагонали матрицы , которая уже определена, 0,780035, см. рис. 7.

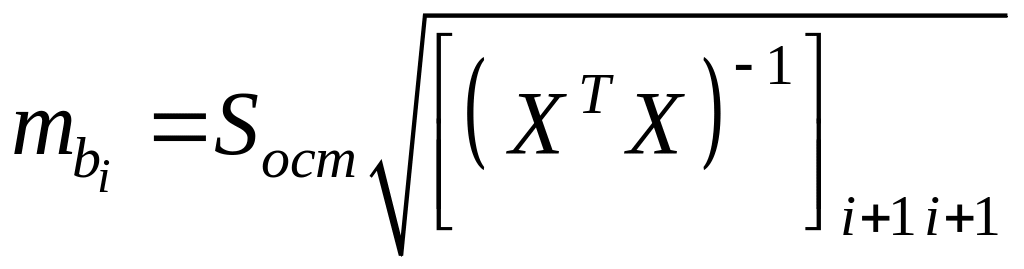– стандартная ошибка коэффициента регрессии ;

– – ый элемент, стоящий на главной диагонали матрицы (0,012591, 0,013613, 0,03132321).

Проверьте значимость коэффициентов регрессии с помощью – критерия Стьюдента.

Статистика 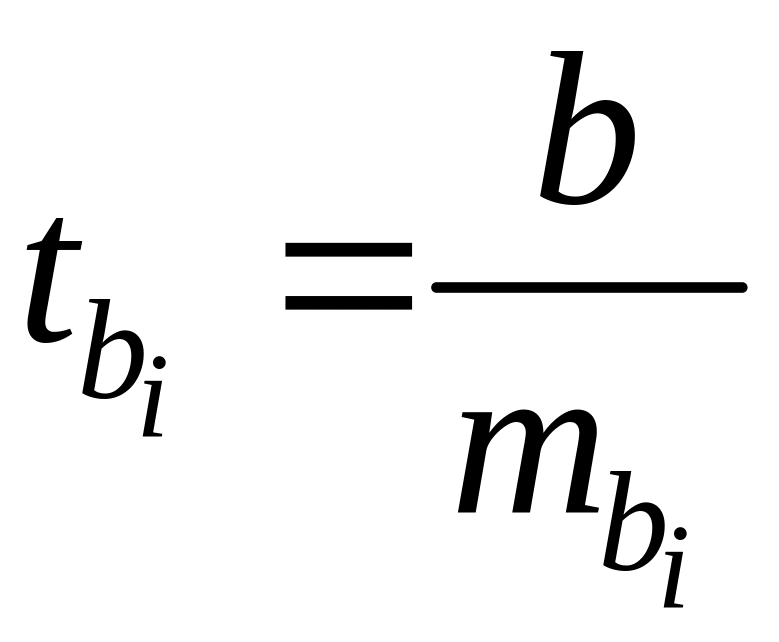при выполнении гипотезы распределена по закону Стьюдента с степенями свободы.

Из таблицы распределения Стьюдента с степенями свободы по заданному уровню значимости выбирается значение как критическая точка, соответствующая двусторонней области.

Тогда:

1) Если , то гипотезу следует отклонить и, следовательно, признать коэффициент b статистически значимым,

2) Если , то гипотезу следует принять и, следовательно, признать коэффициент статистически незначимым.

Статистика при выполнении гипотезы распределена по закону Стьюдента с степенями свободы.

Из таблицы распределения Стьюдента с степенями свободы по заданному уровню значимости выбирается значение как критическая точка, соответствующая двусторонней области.

Тогда:

1) Если , то гипотезу следует отклонить и, следовательно, признать коэффициент b статистически значимым,

2) Если , то гипотезу следует принять и, следовательно, признать коэффициент b статистически незначимым.

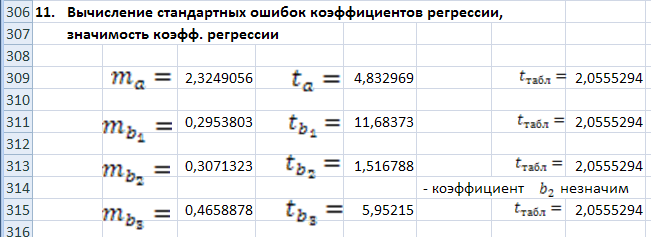
Рис. 14. Результаты вычисления стандартных ошибок коэффициентов регрессии: , , , непосредственно по формулам и проверки значимости коэффициентов регрессии с помощью – критерия Стьюдента.

12. Постройте доверительные интервалы для статистически значимых коэффициентов регрессии.

Рис. 15. Результаты вычисления доверительных интервалов.

1 3. Постройте матрицу , состоящую из выборочных коэффициентов корреляции. Вычислите частные коэффициенты корреляции , , .

Сравните их с парными коэффициентами корреляции, полученными в п. 1. = 0,8808886, = 0,35045284, = 0,606703.

Проверьте статистическую значимость частных коэффициентов корреляции.

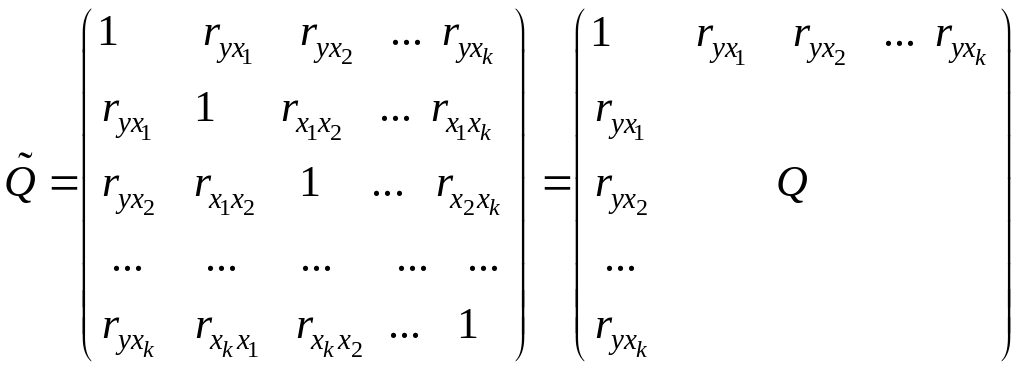
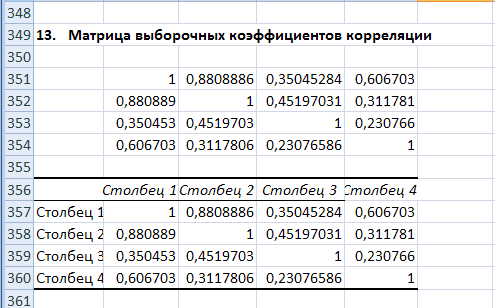
Рис. 16. Матрица выборочных коэффициентов корреляции, построенная с помощью функции КОРРЕЛ (верхняя матрица) и с помощью процедуры КОРРЕЛЯЦИЯ пакета Анализ данных (нижняя матрица).

Выборочным коэффициентом частной корреляции (или просто — частным коэффициентом корреляции) между переменными x_i и x_j при фиксированных значениях остальных k - 2 переменных называется выражение

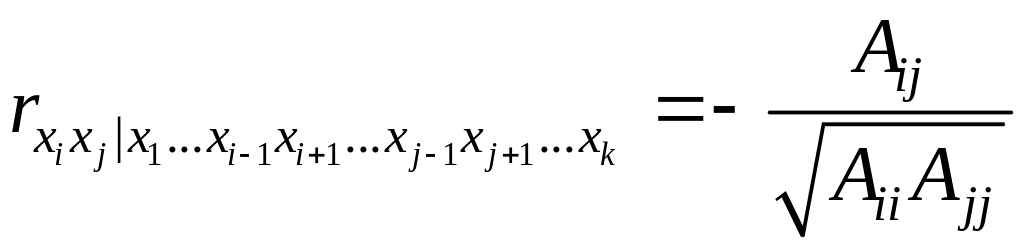
где через обозначены алгебраические дополнения элементов матрицы выборочных коэффициентов корреляции Q.

Значения коэффициентов частной корреляции, как и обычных выборочных коэффициентов парной корреляции, лежат в интервале [-1,1]. Можно сказать, что равенство нулю коэффициента частной корреляции означает отсутствие прямого (линейного) влияния одной переменной на другую.

Выборочным коэффициентом частной корреляции между зависимой переменной y и объясняющей переменной x_j при фиксированных значениях остальных k - 2 переменных называется выражение

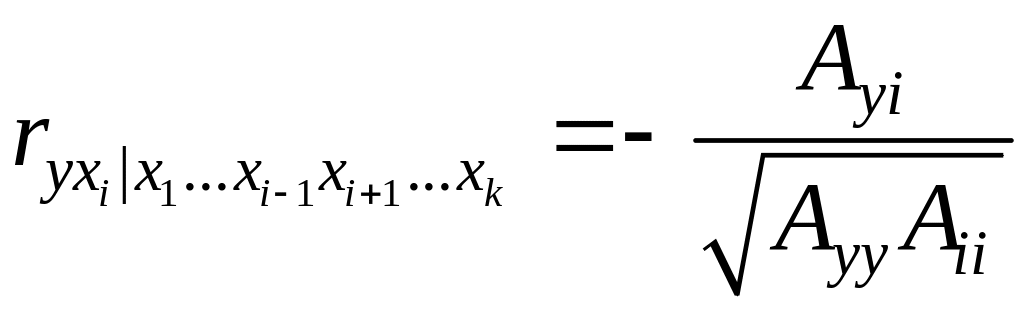
где — алгебраическое дополнение к элементу матрицы ,

— алгебраическое дополнение к элементу (т.е. ),

— алгебраическое дополнение к элементу (заметим, что это единица, стоящая на пересечении i -ой строки и i -го столбца).

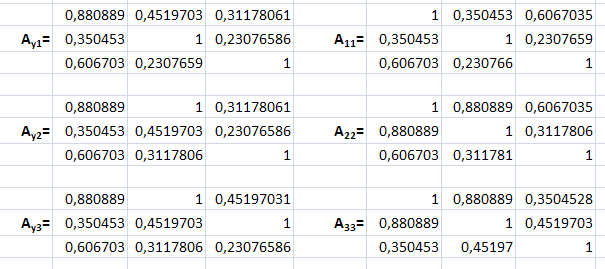
Рис. 15. Вспомогательные матрицы, полученные вычеркиванием соответствующих строк и столбцов из исходной матрица выборочных коэффициентов корреляции, для вычисления определителей.

Рис. 16. Коэффициенты частной корреляции между зависимой переменной y и объясняющей переменной x_i , “очищенные” от влияния остальных факторов. = 0,8808886, = 0,35045284, = 0,606703.