Закон парности касательных напряжений

Закон парности касательных напряжений устанавливает зависи­мость между величинами и направлениями касательных напряжений, действующих по взаимно перпендикулярным площадкам элементар­ного параллелепипеда.

Р ассмотрим элементарный параллелепипед (рис. 2.3.2) и запишем для него уравнение равновесия в виде суммы моментов сил относи­тельно оси Oz. Учтем, что нормальные напряжения взаимно уравно­вешивают друг друга, а момент относительно оси Oz создают только напряжения τ_ху и τ_ух, действующие на правой и верхней гранях па­раллелепипеда. На этих гранях напряжения создают силы τ_ху(dydz) и τ_ху(dxdz), следовательно

Очевидно, что из этого уравнения получается равенство

τ_ху = τ_ух

которое выражает закон парности касательных напряжений: на любых взаимно перпендикулярных площадках, касательные напряже­ния, направленные к линии пересечения площадок, равны по величине и стремятся вращать элемент в противоположные стороны.

Напряжения на наклонных площадках

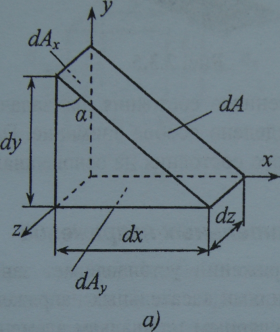
Рассечем элементарный параллелепипед наклонным се­чением, перпендикулярным к плоскости Оху, на две части и рассмот­рим одну из частей - элементарную призму (рис. 2.3.6,а). Положение наклонной площадки призмы будет определяться углом а, который образует нормаль к этой площадке с осью Ох (рис. 2.3.6,б).

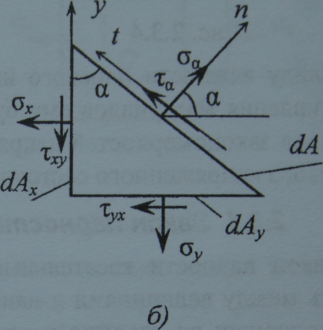К ак видно из рис. 2.3.6,б для площадей граней призмы справедли­вы зависимости:

dA_y =dAsina, dA_x=dAcosa. (2.3.1)

Напряжения, на наклонной площадке σ_a и τ_а найдем из условий равновесия треугольной призмы. Спроектируем действующие на гра­нях призмы силы на оси п и t (рис. 2.3.6,б):

Подставляя в эти уравнения выражение (2.3.1) для dA_x, dA_y со­кращая на dA, с учетом того, что τ_ху = τ_ух, 2sinacosa = sin2a, cos² a - sin² a = cos 2a, получим

(2.3.2)

(2.3.3)

Формулы (2.3.2), (2.3.3) выражают закон изменения напряжений в зависимости от угла наклона площадки a.

Подставляя в соотношение (2.3.2) вместо а угол a+90°, получим

(2.3.4)

Складывая равенства (2.3.2) и (2.3.4), найдем

Таким образом, получили, что в данной точке сумма нормальных напряжений, действующих на любых двух взаимно перпендикулярных площадках, - величина постоянная.

Главные напряжения

Как видно из формулы (2.3.2), величина нормального напряжения зависит от угла наклона площадки а. При некотором значении a = a₀ величина нормального напряжения будет наибольшей. На ос­новании равенства (2.3.5) можно заключить, что на площадке, прохо­дящей под углом а₀ +90° нормальное напряжение будет минималь­ным. Следовательно, максимальные σ_max и минимальные σ_min нор­мальные напряжения действуют на взаимно перпендикулярных пло­щадках.

Экстремальные нормальные напряжения в точке называются глав­ными напряжениями. Площадки, на которых действуют σ_max и σ_min называют главными площадками.

Для определения главных напряжений σ_max и σ_min, а также угла

наклона главных площадок используем условие экстремума σ_a:

С учетом формулы (2.3.2), условие (2.3.6) записывается в следую­щем виде:

Учитывая, что 2 sin a cos a = sin 2a, получим

(2.3.7)

Полагая в последнем выражении a = a₀ находим

(2.3.8)

Используя это уравнение можно определять угол наклона главной площадки а₀.

Так как главные площадки взаимно перпендикулярны, вторая главная площадка будет наклонена под углом а₀ +90°.

Сравнивая выражения (2.3.3) и (2.3.7) можно заключить, что если выполняется условие экстремума σ_a (2.3.6), то τ_а = 0. Следователь­но, на главных площадках касательные напряжения равны нулю.

Можно показать, что главные напряжения определяются по фор­мулам

В общем случае напряженного состояния площадки, на которых касательные напряжения равны нулю, называются главными пло­щадками, а действующие по этим площадкам нормальные напряже­ния - главными напряжениями.

Г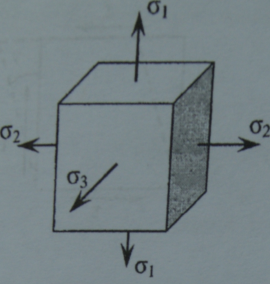 лавные напряжения обозначаются σ1, σ2, σ3, причем σ1 σ2 σ3. Элемент, выделенный главными площадками, изобра­жен на рис.

В случае плоского напряженного состояния также часто использу­ются обозначения σ1= σmax, σ2= σmin, σ3=0.

Р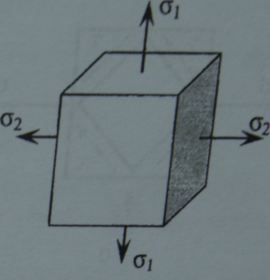 ассмотрим параллелепипед, образованный главными площадками (рис.). В этом случае можно положить σx= σ1, σy= σ2, τxy=0 и формулы (2.3.2), (2.3.3) принимают вид:

(2.3.9)