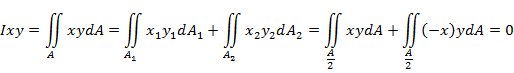Потенциальная энергия деформации

Потенциальная энергия деформации стержня - это энергия, нако­пленная в теле при его деформировании под действием внешних сил.

К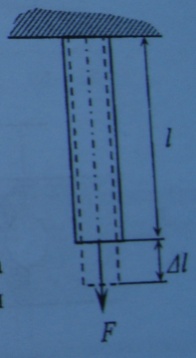 ак было установлено, в соответствии с законом Гука, при дейст­вии на стержень продольной силы F (рис.) возникает удлинение ∆L=FL/EA

Изменение силы на величину dF приводит к изменению удлине­ния на величину d∆L = dF*(L/EA). При этом сила F совершает элементарную работу dW = Fd∆L = F*(dFL/EA).

Суммируя элементарные работы, которые совершает сила при из­менении от 0 до N, получаем

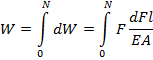
После подстановки, находим

Вследствие закона сохранения энергии, работа продольной силы N равна потенциальной энергии деформации Uo, следовательно

Удельной потенциальной энергией деформации U называется ве­личина потенциальной энергии деформации, накопленной в единице объема тела.

Учитывая, что при растяжении и при сжатии деформации равно­мерно распределяются по стержню, а его объем V = Аl, получаем удельную потенциальную энергию.

4. Геометрические характеристики плоских фигур

На величины σ и ∆L влияют размеры и не оказы­вает влияния форма поперечного сечения стержня. Площадь попереч­ного сечения А полностью характеризует прочность и жесткость стержня. Эта величина является простейшей геометрической характе­ристикой поперечного сечения стержня.

При других видах деформаций стержня на величины напряжений и перемещений существенное влияние оказывает форма поперечного сечения стержня. Поэтому возникает необходимость для расчетов ис­пользовать различные геометрические характеристики плоских фигур.

Статические и осевые моменты инерции фигуры

Р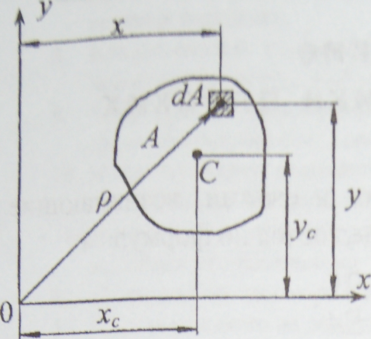 ассмотрим фигуру площади А (рис. ). Выделим на ней эле­ментарную площадку dA с координатами х, у и радиусом-вектором р.

Статическими моментами инерции фигуры относительно осей х и у называются величины S_x и S_y, определяемые интегралами:

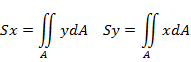
где х, у - расстояния от элементарной площадки dA до осей Ох и Оу.

Можно показать, что координаты центра тяжести фигуры х_с, y_c вычисляется по формулам:

Оси, проходящие через центр тяжести фигуры называются цен­тральными осями. Очевидно, что для центральных осей х_с и у_с =0 и из последних формул следует, что для центральных осей статические моменты инерции фигуры равны нулю (S_x =S_y = О).

Величины называются осевыми моментами инерции фигуры относительно осей хиу соответственно.

Интеграл по площади фигуры называется полярным моментом инерции.

Величина - центробежный момент инерции фигуры.

Учитывая, что р² = х² +у² получаем

Следовательно Ip=Ix+Iy

т.е. сумма осевых моментов инерции сечения равна полярному моменту инерции этого сечения.

Осевые и полярные моменты инер­ции всегда положительны, центро­бежный момент инерции может быть положительным, отрицательным, равным нулю.

Ц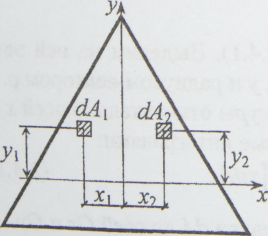 ентробежный момент инерции фигуры относительно осей, хотя бы одна из которых является осью симметрии, равен нулю. Действи­тельно, для симметричной фигуры всегда можно выделить два эле­мента ее площади (рис.), которые имеют одинаковые ординаты y₁ =у₂ = у и равные по величине, но противоположные по знаку абс­циссы х₁= х и х₂ = - х. В этом случае