Испытание металлов на растяжение

Многие свойства материалов выявляются при испытаниях мате­риалов на растяжение до разрушения. Экспериментально определяют­ся механические характеристики, позволяющие оценить прочностные и пластические свойства материала.

Д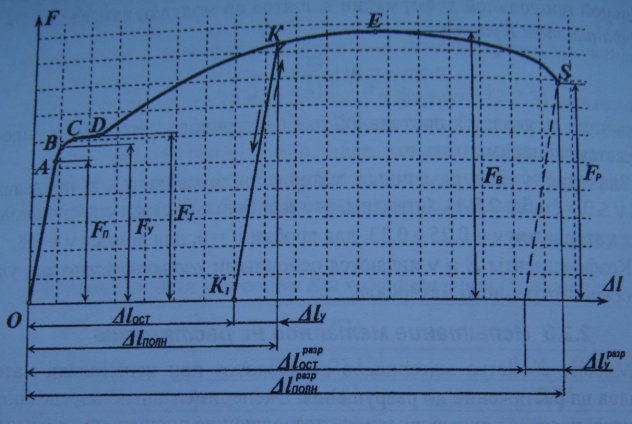 ля проведения опытов на растяжение используют специальные образцы, которые закрепляются в захватах машины и под­вергается деформированию вплоть до разрушения. При этом зависи­мость, между растягивающей силой F и величиной продольной де­формации ∆L записывается в виде графика (рис), который на­зывается машинной диаграммой растяжения материала.

Для изучения свойств материала удобно пользоваться диаграммой растяжения, устанавливающей связь между нормальным напряжением σ и деформацией ε. Эту диаграмму называют условной диаграммой растяжения и при ее построении используют формулы:

ε=∆L/L0, σ=F/A

г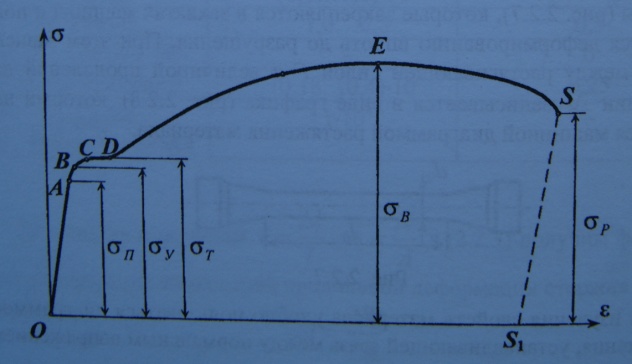 де F- растягивающая сила, Ао - первоначальная площадь поперечно­го сечения образца, L₀ - длина образца, ∆L - удлинение. Величины F и ∆L берутся с машинной диаграммы растяжения.

Рассмотрим диаграмму растяжения образца из малоуглеродистой стали Ст.З (рис). На этой диаграмме необходимо отметить точки A,B,C,D,E,S.

Начальный участок диаграммы OA - прямая наклонная линия. На­пряжения σ в образце прямо пропорциональны деформации ε, соблю­дается закон Гука: σ = Eε. Точке А соответствует напряжение σ_п – предел пропорциональности.

Пределом пропорциональности называется наибольшее напряже­ние, при котором деформация в материале прямо пропорциональна нагрузке: σ_п=Fп/A₀

Выше точки А линия диаграммы искривляется, закон Гука не вы­полняется. Вблизи точки А, на криволинейном участке диаграммы, можно отметить точку В, соответствующую пределу упругости σ_у.

Пределом упругости называется наибольшее напряжение, при ко­тором в материале возникает только упругая деформация: σ_у=Fу/A₀

Начиная от точки С, диаграмма имеет горизонтальный (или почти горизонтальный) участок, которому соответствует предел текучести σ_т. На этом участке деформации растут без увеличения нагрузки - материал как бы течет.

Пределом текучести называется напряжение, при котором дефор­мация возрастает без заметного увеличения нагрузки: σ_т=Fт/A₀

Горизонтальный участок диаграммы CD называют площадкой те­кучести, возникновение которой связано с явлением текучести. Пло­щадка текучести ярко выражена только для малоуглеродистых сталей.

Точке Е диаграммы соответствует напряжение σ_в - предел проч­ности.

Пределом прочности называется напряжение, соответствующее максимальной нагрузке, которую выдержал образец не разрушаясь: σ_в=Fв/A₀

До достижения предела прочности продольные и поперечные де­формации образца равномерно распределяются по его длине. После достижения точки Е диаграммы материал в основном деформируется в одном наиболее слабом месте, где начинается образовываться шейка - местное значительное сужение образца. Образец до и после дефор­мации показан на рис.

З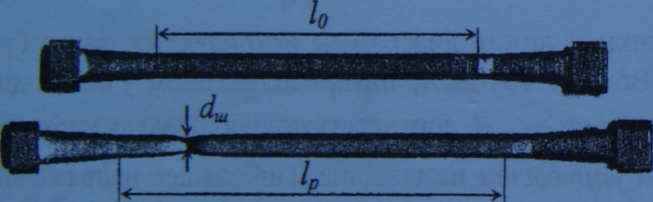 а точкой Е нагрузка снижается, что объясняется уменьшением поперечного сечения шейки. Разрыву образца на диаграмме соответст­вует точка S.

Е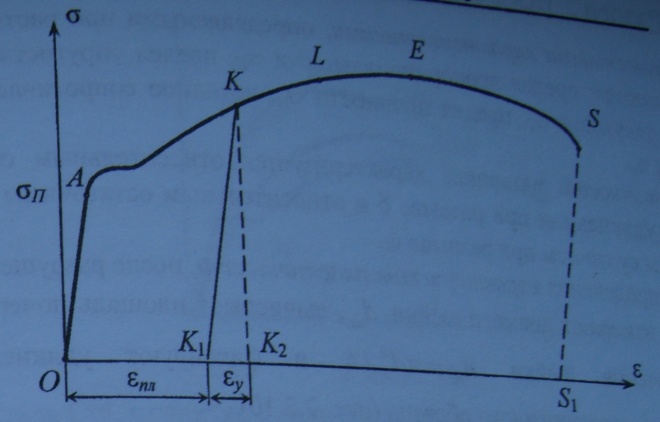 сли, начиная с некоторой точки К диаграммы (рис.), раз­гружать образец, то линия диаграммы будет представлена прямой KK1, параллельной прямой OA. Отрезок ОК1 равен величине пласти­ческой (остаточной) деформации ε_пл, а отрезок К1К2 - упругой де­формации ε_у. Полная деформация при напряжении, соответствующе­му точке К: ε= ε_у+ ε_пл

Если вновь нагружать образец, то вначале линия диаграммы будет практически прямой K1K, а затем такой, как будто не было разгрузки и повторного нагружения. Следовательно, при нагружении образца вы­ше предела текучести и последующей его разгрузке материал образца изменил свои свойства: отсутствует площадка текучести, повысился предел пропорциональности.

Такое изменение свойств металла носит название наклепа. Наклеп может возникнуть не только при растяжении, но и при других видах деформации.

Высокоуглеродистые стали и некоторые другие материалы, не имеют площадки текучести. Предел текучести для этих материалов принимается условно равным напряжению, при котором остаточная деформация образца составляет 0,2%. Эта величина называется услов­ным пределом текучести и обозначается ε_0,2.

Прочностными характеристиками, определяемыми при растяжении являются: предел пропорциональности σ_п, предел упругости σ_у, предел текучести σ_т, предел прочности σ_в, истинное сопротивление разрыву σ_р.

Пластичность материала характеризуется относительным оста­точным удлинением при разрыве δ и относительным остаточным по­перечным сужением при разрыве ᴪ.

Для определения характеристик пластичности, после разрушения образца, измеряют диаметр шейки d_ш, вычисляют площадь попереч­ного сечения шейки A_ш = (pi*(d_ш)^2)/4 фиксируют удлинение ∆L_р = L_p + L₀ разрушенного образца (рис. Выше с образцами).

Относительное остаточное удлинение δ при разрыве определяет­ся по формуле:

δ=(∆L_р/ L₀)*100%

Относительное остаточное поперечное сужение ᴪ равно:

ᴪ=((A0-Aш)/А0)*100%

В зависимости от величин δ и ᴪ, материалы условно делятся на пластичные и хрупкие. Материал считается пластичным, если от­носительная остаточная деформация δ больше 5%. Для стали марки СтЗ относительная остаточная деформация 5 >21%, у высокопрочных сталей эта величина снижается до 7... 10%.

С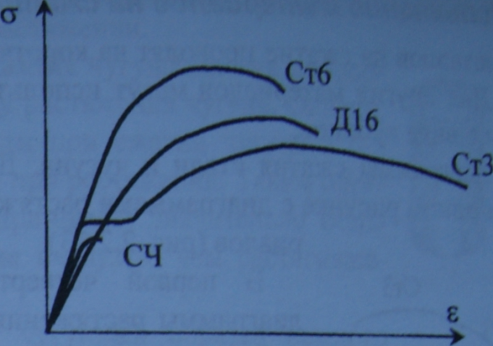 равним диаграммы растяжения для различных материалов. На рис. приведены диаграммы для серого чугуна (СЧ), для сталей марок СтЗ, Стб и для алюминиевого сплава Д16.

Сталь Ст6, в отличие от стали СтЗ, обладает значительно более вы­сокими характеристиками прочности. Площадка текучести у нее от­сутствует, шейка при разрыве не так ярко выражена, как у стали СтЗ. Остаточная деформация при разрыве стали марки Ст6 значительно меньше, чем у стали СтЗ.

Диаграмма растяжения серого чугуна - почти прямая, слегка вы­пуклая линия. Разрыв чугунного образца происходит без образования шейки при малых остаточных деформациях

Конструкционные материалы условно делятся на две группы: пла­стичные и хрупкие.

Пластичные материалы (стали, медь, алюминиевые сплавы) имеют диаграммы растяжения, подобные диаграмме стали СтЗ (иногда без площадки текучести) и аналогичную форму разрушения.

Хрупкие материалы (бетон, кирпич) имеют диаграммы растяжения, подобные диаграмме чугуна, и сходную форму разрушения.

Деление материалов на хрупкие и пластичные носит условный ха­рактер, т. к. при некоторых условиях, хрупкие материалы могут при­обретать свойства пластических материалов и наоборот. Например, образец из пластичной стали при низкой температуре разрушается как хрупкий материал, без образования шейхи, а стекло при всестороннем сжатии приобретает свойства пластичного материала.